通过神经结构搜索进行视频动作识别
paper题目:VIDEO ACTION RECOGNITION VIA NEURAL ARCHITECTURE SEARCHING
paper是奥卢大学发表在ICIP 2019的工作
paper地址:链接
ABSTRACT
深度神经网络在视频分析和理解方面取得了巨大成功。然而,设计高性能神经架构需要大量的努力和专业知识。在本文中,我们首次尝试让算法自动设计用于视频动作识别任务的神经网络。具体来说,时空网络是在由有向无环图建模的可微空间中开发的,因此可以执行基于梯度的策略来搜索最佳架构。尽管如此,它在计算上是昂贵的,因为评估每个体系结构候选者的计算负担仍然很重。为了缓解这个问题,我们针对视频输入引入了一种时间段方法,以在不丢失全局视频信息的情况下降低计算成本。对于架构,我们通过引入伪 3D 运算符在高效的搜索空间中进行探索。实验表明,在具有挑战性的 UCF101 数据集上,我们的架构在从头开始训练协议下的表现优于流行的神经架构,令人惊讶的是,其参数仅为其手动设计对应物的大约百分之一。
索引词——自动机器学习,神经结构搜索,视频动作识别
1. INTRODUCTION
视频动作识别 [1] 是视频分析和理解的热门话题,已经引起了学术界和工业界的广泛关注,因为它对行为分析 [2]、安全和视频情感等许多潜在应用具有重要价值计算[3]。一方面,新的大规模数据集,如 Kinetics [4]、SomethingSomething [5],对视频动作识别做出了巨大贡献。另一方面,视频分析和理解从深度神经网络的最新进展中受益匪浅,深度神经网络已经成功应用于各种任务,如目标检测 [6] 和机器翻译。然而,设计一个高性能的神经网络结构是一项艰巨的工作。它需要人类专家大量的时间和努力。具体来说,在动作识别任务中,为了获得令人满意的性能,应考虑远程时空连接。因此,它不可避免地导致复杂的网络架构和昂贵的计算成本。此外,必须为这样的网络提供大量训练数据。
最近,神经架构搜索 (NAS) [7] 显示出优于手动设计的神经架构。在图像分类中,NASNet [8] 和 AmoebaNet [9] 等自动设计的架构优于 VGG [10] 和 ResNet [11] 等流行的人工设计网络。在语义图像分割中,AutoDeeplab [12] 即使没有预训练程序也表现良好。这些有前途的进展主要得益于当前强大的计算能力、精细的搜索空间 [13] 以及强化学习 [7]、进化算法 [9] 和梯度方法 [14] 等搜索策略的效率。然而,涉及的任务仅限于文本和图像等低维输入的情况。
在本文中,我们旨在实现用于动作识别的自动神经架构设计。在 NAS 令人鼓舞的进展的推动下,我们提出以一种高效的方式将 NAS 引入到动作识别任务中。首先,采用类似于时间段网络(TSN)[15]的视频处理方案来捕获全局时间信息并降低计算成本。它还有助于数据扩充。其次,为了表征视频中的时空动态,我们通过在具有伪 3D [16] 运算符的搜索空间中分别处理空间和时间特征,提供了一种搜索 3D 神经运算符的有效解决方案。第三,我们引入了一个有向无环图来对搜索空间进行建模,并将离散空间松弛为连续和微分的空间[14]。因此,与之前需要数千 GPU 天进行搜索的计算资源相比,它能够以小数量级的计算资源实现极具竞争力的性能。
本文的贡献有三方面:首先,据我们所知,这是首次尝试针对视频动作识别问题自动设计时空神经网络。其次,我们设计了一个连续的伪 3D 神经网络搜索空间,可以在其中使用无代理策略探索高效算子。最后,我们在 UCF101 [17] 数据集上评估了所提出的方法。与没有预训练的流行动作识别神经架构相比,我们搜索到的架构仅用大约百分之一的参数就获得了最佳性能。
2. PROPOSED METHODS
在本节中,我们将详细介绍要搜索的模块化架构 C \mathcal{C} C和搜索策略。在这里,我们搜索单个 ( 2 + 1 ) D (2+1) \mathrm{D} (2+1)D卷积模块单元并重复多次以构建神经网络。在搜索过程中,我们构建了一个浅层网络 N ( C ) \mathcal{N}(\mathcal{C}) N(C),以在搜索空间中进行探索。
对于视频动作识别任务,引入了一种类似 TSN 的方案来处理各种长度的输入剪辑。它不仅降低了计算成本,而且有助于捕获全局信息和数据扩充。我们将剪辑统一分割成 N s N_s Ns个片段。在每个片段中,我们随机采样 N r N_r Nr帧,并按照原始顺序将它们重新组合以形成新的剪辑。然后将这些固定长度 ( N s × N r ) \left(N_s \times N_r\right) (Ns×Nr)的片段用作我们模型的输入。
2.1. Neural module architecture
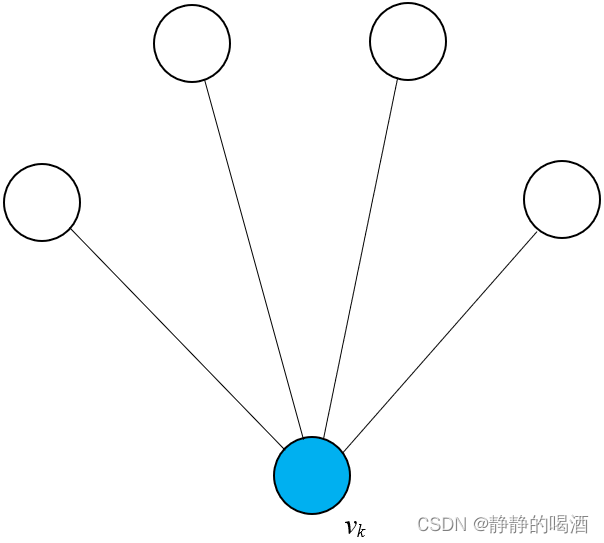
如图 1 所示,我们构建了一个有向无环图来对神经模块单元 C \mathcal{C} C进行建模。假设 n n n个节点的 C \mathcal{C} C是我们神经网络中用于视频动作识别的基本单元。然后搜索过程是从一组候选算子 O \mathcal{O} O中找出这 n n n个节点及其对应的变换函数之间的连接,以优化性能。
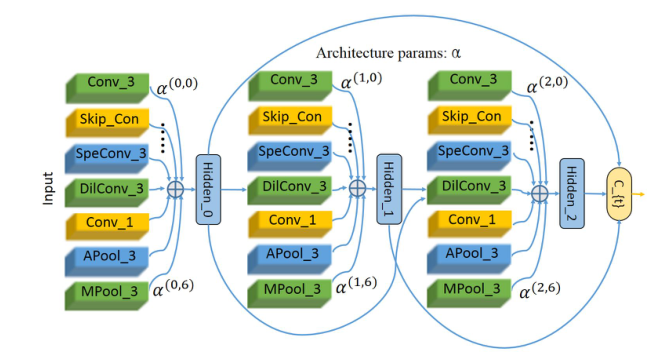
图 1:待搜索的神经模块概览。模块的架构由不同的节点(Hidden i)连接和运算符决定。该模块包含三个节点。连接它们的输出形成模块输出。对于节点之间的每个连接,有八个候选运算符,详见表 1 底部。在连续搜索空间中,每个运算符的贡献由权重 α ( k , j ) \alpha^{(k, j)} α(k,j)参数化。请注意,为了便于解释,此图中省略了前两个模块输出的连接。

连接。在这里,连接充当数据流。对于每个节点,即图 1 中的“Hidden_i”,我们将其之前节点的所有输出作为其输入。此外,从网络层面来看,前两个模块的输出也作为其输入(图1中未显示)。因此,总共有 n n n个节点的模块内有 M = ( n + 1 ) ( n + 2 ) 2 − 1 M=\frac{(n+1)(n+2)}{2}-1 M=2(n+1)(n+2)−1个连接。对于每个节点的输出,在其不同的输入期间进行逐元素加法。最后,将这些节点的所有输出连接起来作为模块输出 C − { t } \mathcal{C}_{-}\{t\} C−{t}。
操作。所有的连接都充满了来自 O \mathcal{O} O的一个或多个运算符。在这里,我们将每个算子解耦为二维空间算子和一维时间算子,因为与三维算子相比,(2+1)D卷积滤波器的参数较少,但可以获得更好的性能。在本文中, O \mathcal{O} O中的初始算子集由8个候选算子组成,它们被列在表1的底部八行中。这里,最大或平均池层和RELU-CONV-BN块在现代人工设计的网络中普遍存在。'SpeConv_3’是由三个1D滤波器实现的。‘DilConv_3’ 的空间视角为 5 × 5 5 \times 5 5×5。出于计算上的考虑,我们将所有的运算符都设置为相对较小的核大小。
为了从
O
\mathcal{O}
O中找到最佳运算符,如 [14],我们将它们全部引入每个连接并使用架构参数
α
\alpha
α对它们进行建模。然后对于每个连接,在每个加权运算符的输出之间进行逐元素加法。因此,减少了搜索过程以找到最佳架构参数
α
\alpha
α,从而最大限度地提高验证数据的性能。在搜索结束时,可以通过 softmax 等函数获得离散架构。因此,搜索策略是在每个迭代步骤调整每个算子的贡献并找出网络架构参数
α
=
{
α
(
k
,
j
)
}
\alpha=\left\{\alpha^{(k, j)}\right\}
α={α(k,j)},对于
k
=
0
,
…
,
M
−
1
,
j
=
0
,
.
.
∣
O
∣
−
1
k=0, \ldots, M-1, j=0, . .|\mathcal{O}|-1
k=0,…,M−1,j=0,..∣O∣−1,最小化任务损失,公式如下:
α
∗
=
arg
min
α
L
valid
(
Θ
(
α
)
,
α
)
.
(
1
)
\alpha^*=\arg \min _\alpha \mathcal{L}_{\text {valid }}(\Theta(\alpha), \alpha) .(1)
α∗=argαminLvalid (Θ(α),α).(1)
在这里,我们引入了
N
(
C
)
\mathcal{N}(\mathcal{C})
N(C)中的参数共享方案,因此
Θ
\Theta
Θ是网络内的权重,由每个架构候选者共享。
L
valid
\mathcal{L}_{\text {valid }}
Lvalid 是验证集上的损失函数。为了更好地评估架构,
Θ
\Theta
Θ还将在每次迭代时根据训练数据进行更新。让
L
train
\mathcal{L}_{\text {train }}
Ltrain 表示训练的损失函数。显然,损失由模块架构
α
\alpha
α和网络权重
Θ
\Theta
Θ共同决定。求解公式(1)意味着找到最优的
α
\alpha
α,其中权重
Θ
\Theta
Θ最小化
L
train
\mathcal{L}_{\text {train }}
Ltrain 。这个双层问题很难,因为它们是相互依赖的,更准确地说,是嵌套的。我们将在下一节中讨论它。
2.2. Search Strategy
在本小节中,我们详细阐述了优化神经网络架构的搜索策略。
虽然搜索空间被放松为一个连续且有区别的空间,但公式(1) 的优化仍然具有挑战性甚至不可行。主要原因是对于架构
α
\alpha
α的任何变化,都必须通过最小化
L
train
\mathcal{L}_{\text {train }}
Ltrain 来重新计算
Θ
(
α
)
\Theta(\alpha)
Θ(α)。为了减轻这种困难,执行交替迭代近似。更具体地说,给定一个搜索空间,有两个可选步骤来执行此搜索过程:首先,通过最小化
L
train
\mathcal{L}_{\text {train }}
Ltrain 来更新网络权重
Θ
\Theta
Θ,其中架构是固定的。其次,通过固定网络权重最小化
L
valid
\mathcal{L}_{\text {valid }}
Lvalid 来更新网络架构
α
\alpha
α。在此基础上,通过以迭代方式在网络权重和架构参数中的梯度下降步骤之间交替来优化
Θ
\Theta
Θ和
α
\alpha
α。事实上,这个任务与少样本元学习任务[18]非常相似,后者是使用少量数据和训练过程使模型适应新任务。从这个角度来看,神经架构搜索可以被视为一种元学习,其中 NAS 是将在训练数据上训练的网络通过微调架构来传输以适应验证数据。因此,在等式 (1) 中为
Θ
(
α
)
\Theta(\alpha)
Θ(α)采用代理函数。那是
α
∗
=
arg
min
α
L
valid
(
Θ
′
,
α
)
(
2
)
Θ
′
=
Θ
−
ϵ
∇
Θ
L
train
(
Θ
,
α
)
.
(
3
)
\begin{aligned} \alpha^* & =\arg \min _\alpha \mathcal{L}_{\text {valid }}\left(\Theta^{\prime}, \alpha\right)(2) \\ \Theta^{\prime} & =\Theta-\epsilon \nabla \Theta \mathcal{L}_{\text {train }}(\Theta, \alpha) .(3) \end{aligned}
α∗Θ′=argαminLvalid (Θ′,α)(2)=Θ−ϵ∇ΘLtrain (Θ,α).(3)
在这里,
ϵ
\epsilon
ϵ在搜索步骤中是一个非常小的值。通过对架构参数
α
ˉ
\bar{\alpha}
αˉ使用梯度下降法,我们可以找到架构的解决方案。那是
α
=
α
−
γ
∇
α
.
(
4
)
\alpha=\alpha-\gamma \nabla_\alpha .(4)
α=α−γ∇α.(4)
这里
γ
\gamma
γ是学习率,
∇
α
\nabla_\alpha
∇α由式(5)计算:
∇
α
=
∇
α
L
valid
(
Θ
′
,
α
)
−
ϵ
∇
α
,
Θ
2
L
train
(
Θ
,
α
)
∇
Θ
′
L
valid
(
Θ
′
,
α
)
(
5
)
\begin{aligned} \nabla_\alpha= & \nabla_\alpha \mathcal{L}_{\text {valid }}\left(\Theta^{\prime}, \alpha\right)- \\ & \epsilon \nabla_{\alpha, \Theta}^2 \mathcal{L}_{\text {train }}(\Theta, \alpha) \nabla_{\Theta^{\prime}} \mathcal{L}_{\text {valid }}\left(\Theta^{\prime}, \alpha\right) \end{aligned}(5)
∇α=∇αLvalid (Θ′,α)−ϵ∇α,Θ2Ltrain (Θ,α)∇Θ′Lvalid (Θ′,α)(5)
公式 (4) 和 (5) 为我们提供了一个通过 SGD 优化架构的解决方案。然而,它的计算效率不高,因为存在二阶导数,其中矩阵向量积的计算量很大。幸运的是,这里可以使用 Hessianvector 乘积来逼近二阶导数 [14],从而可以显著降低计算复杂度。此外,值得一提的是当
ϵ
→
0
\epsilon \rightarrow 0
ϵ→0,Eq (3) 表明
Θ
′
→
Θ
\Theta^{\prime} \rightarrow \Theta
Θ′→Θ,这意味着二阶导数退化为一阶导数。因此,作为式(5)的一个特例,出于计算考虑,可以去掉式(3)中的一步展开权重操作,这样可以减少大约三分之一的计算成本,在一定损失的情况下在准确性上是宽容的。
3. EXPERIMENTS
在本节中,我们研究了所提出的设计动作识别网络的自动方法,以证明其优于其他著名动作识别架构的优势,例如 3D-ResNet [19]、C3D 网络 [20] 和 STC-ResNet [21]。我们在具有挑战性的动作识别数据集 UCF101 上评估我们的算法,该数据集是一个包含 101 个类的 13320 个视频剪辑的修剪数据集,使用从头开始训练协议。从头开始训练协议是常用的,对于有限数据或有限计算资源的问题具有重要价值。由于计算资源的限制,没有考虑其他架构,例如 I3D [22] 和 TSN,它们是具有额外输入模式的双流方法或在另一个更大的数据集上预训练的。
实施。设计自动动作识别网络有两个阶段:训练网络和更新架构,这两个阶段交替执行。我们在 UCF101 的 split 1 上搜索网络。在搜索过程中,我们构建了三层网络 N ( C ) \mathcal{N}(\mathcal{C}) N(C),每一层都由一个相同的模块 C \mathcal{C} C构建,这就是要搜索的模块。我们用四个通道初始化第一个模块,并将隐藏节点的数量 n n n设置为四个,作为准确性和效率之间的权衡。对于具有不同分辨率的特征输入,我们在模块之前添加了一个额外的特征图适配层。一旦需要降低特征图分辨率,输出通道就会相应加倍。该网络将 8 个大小为 112 × 112 112 \times 112 112×112的 RGB 帧作为输入。因此,对于视频输入预处理,我们设置分段数 N s = 4 N_s=4 Ns=4和随机样本数 N r = 2 N_r=2 Nr=2。采用归一化、随机水平翻转和随机裁剪等其他数据增强方法。对于目标函数,UCF101 上的分类任务采用交叉熵损失。为了搜索架构,整个搜索过程为 50 个 epoch,因此我们选择了一个相对较大的学习率。我们还降低了每次迭代的学习率。使这个搜索过程更有效的是搜索模型在每次验证后都不会被丢弃。
完成搜索过程后,我们将从头开始构建和训练最终网络。如前所述,我们用返回的搜索结果 α \alpha α构建网络,如图 1 所示。这里,对于每个节点,我们根据 α \alpha α保留前 2 个连接,然后根据他们的贡献。这里,在 α \alpha α上采用 softmax 函数来评估每个算子的贡献。然后可以通过离散架构构建网络,如图 2 所示。对于网络的深度,我们研究了不同的重复次数,发现当深度设置为 6 时网络表现最佳。每两层,我们将特征图分辨率沿宽度和高度方向降低两倍。因此,我们将特征图的通道加倍。整个训练过程设置如下:我们将第一个模块初始化为 8 个通道,训练迭代次数为 600 轮,学习率为 0.025,并通过迭代步数的余弦函数进行消减。该网络以 0.9 的动量、0.0003 的权重衰减和 72 的小批量进行训练。对于测试处理,我们的模型预测每个视频剪辑的分数而无需额外聚合。对于每个输入剪辑,我们采样八帧,仅对输入应用中心裁剪。
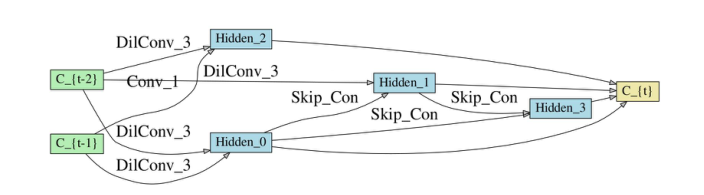
图 2:通过我们的方法搜索的神经结构。在这里,我们根据 α \alpha α为每个节点保留两个连接。前两个模块 C − { t − 1 } \mathcal{C}_{-}\{t-1\} C−{t−1}和 C − { t − 2 } \mathcal{C}_{-}\{t-2\} C−{t−2}的输出被作为当前模块的输入。这四个节点的所有输出连接起来形成最终输出 C − { t } \mathcal{C}_{-}\{t\} C−{t}。
结果。当 50 次搜索迭代完成后,我们根据其性能选择最佳架构。我们在单个 Nvidia V100 GPU 上执行搜索过程。在 UCF101 上完成此搜索过程大约需要 25 个小时。搜索到的架构如图2所示。这表明该架构更喜欢具有更大视野的算子。
得到搜索结果后,我们通过重复这个神经模块单元来构建一个六层的网络。然后,我们对 600 个 epoch 的训练数据进行训练并进行测试。表 2 显示了 UCF101 与 3D-convNet、3D-ResNet 18、3D-ResNet 101 和不同种类的 STC-ResNet 网络相比的动作识别结果。结果表明,与该表中的任何其他模型相比,我们的方法使用更少的参数实现了更好的准确性。例如,3D-ConvNet,这是一种非常常用的架构,在参数大小方面比我们的网络大一百倍。尽管如此,我们的模型在识别准确率方面比它高出 7%。

4. CONCLUSION
在本文中,我们首次对动作识别任务执行神经架构搜索。具体来说,我们通过有向无环图对神经网络进行建模,并在连续搜索空间中有效地搜索时空神经架构。我们证明了我们的方法在从头开始协议训练下优于其他流行模型,模型尺寸小得惊人。更具体地说,我们的方法在 UCF101 数据集上提高了 10% 以上的准确性,其大小约为 3D-convNet 和 3D-ResNet 等著名模型的百分之一。在未来的工作中,我们计划将所提出的方法应用于其他计算机视觉任务





![[附源码]Python计算机毕业设计Django勤工俭学管理小程序](https://img-blog.csdnimg.cn/a98fb6e356794bada2942059b852ba57.png)