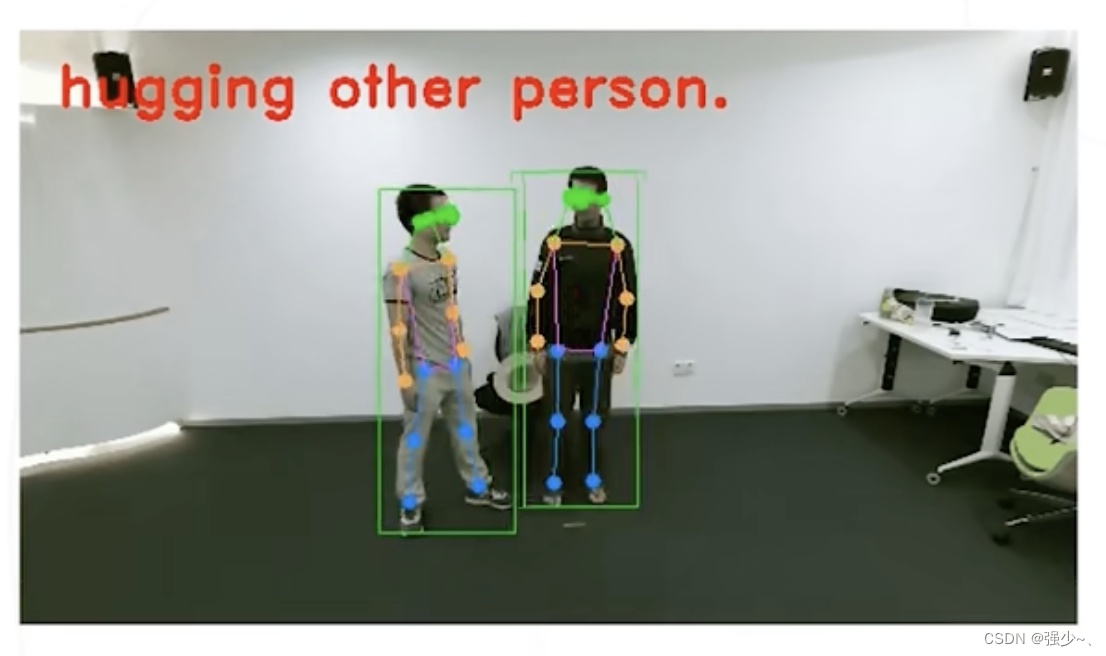
提示：文章写完后，目录可以自动生成，如何生成可参考右边的帮助文档

---

提示：以下是本篇文章正文内容，下面案例可供参考

一、实验目的

1、理解平面电磁波的频率、角频率、周期、波数、波长、初始相位、波阻抗的
物理含义。
2、通过实验熟悉如何辨识平面电磁波的传输方向
3、理解均匀平面波电场分量的大小、相位差对电磁波极化产生的影响。
4、通过实验加深对电磁波传输的极化特性的辨识。

二、实验原理和实验内容

掌握线极化、左旋圆极化、右旋圆极化、椭圆极化的判断。

三、案例运行

例1：电磁波传输问题的动态仿真，编写 MATLAB 程序实现线极化平面波传输问题的动态仿真。程序如下

u0=4*pi*1e-7;%自由空间中的磁导率
e0=1e-9/(36*pi);%自由空间中的电介质常数
Yita0=(u0/e0)^0.5;%自由空间中的波阻抗
f=0.5e8;%电磁波的频率
w=2*pi*f;%电磁波角频率
k=w*(u0*e0)^0.5;%波数
sign = -1;%波数前面的正负号
phi_E=0;%初始相位设为 0
phi_H=0;
EE=20;%电场幅度
HH=EE/Yita0;
z=0:0.1:20;%传播方向上的采样点
m0=zeros(size(z));
figure
for t=0:1:300 %为了消除波数与频率之间的数量级带来的影响，时间单位为 ns
Ex=EE*cos(sign*k*z+w*t*1e-9+phi_E); %电场强度值
Hy=HH*cos(sign*k*z+w*t*1e-9+phi_H); %磁场强度值
plot3(z,Ex,m0,'b','LineWidth',2);%绘制电场传播曲线
hold on
plot3(z,m0,Hy,'r','LineWidth',2);%绘制磁场传播曲线
hold off
xlabel('z')
ylabel('Ex')
zlabel('Hy')
title(['平面电磁波传播示意图','t=',num2str(t),'ns'],'fontsize',14)
set(gca,'fontsize',12)
drawnow
frame=getframe(1);%获取当前图像
end

仿真结果如下：

调整例题中不同的频率进行数值实验，例题中频率是 500MHz，分别修改为200MHz 和 800MHz,分析波长的变化

在200MHz时：

u0=4*pi*1e-7;%自由空间中的磁导率
e0=1e-9/(36*pi);%自由空间中的电介质常数
Yita0=(u0/e0)^0.5;%自由空间中的波阻抗
f=0.2e8;%电磁波的频率
w=2*pi*f;%电磁波角频率
k=w*(u0*e0)^0.5;%波数
sign = -1;%波数前面的正负号
phi_E=0;%初始相位设为 0
phi_H=0;
EE=20;%电场幅度
HH=EE/Yita0;
z=0:0.1:20;%传播方向上的采样点
m0=zeros(size(z));
figure
for t=0:1:300 %为了消除波数与频率之间的数量级带来的影响，时间单位为 ns
Ex=EE*cos(sign*k*z+w*t*1e-9+phi_E); %电场强度值
Hy=HH*cos(sign*k*z+w*t*1e-9+phi_H); %磁场强度值
plot3(z,Ex,m0,'b','LineWidth',2);%绘制电场传播曲线
hold on
plot3(z,m0,Hy,'r','LineWidth',2);%绘制磁场传播曲线
hold off
xlabel('z')
ylabel('Ex')
zlabel('Hy')
title(['平面电磁波传播示意图','t=',num2str(t),'ns'],'fontsize',14)
set(gca,'fontsize',12)
drawnow
frame=getframe(1);%获取当前图像
end

在800MHz时：

u0=4*pi*1e-7;%自由空间中的磁导率
e0=1e-9/(36*pi);%自由空间中的电介质常数
Yita0=(u0/e0)^0.5;%自由空间中的波阻抗
f=0.8e8;%电磁波的频率
w=2*pi*f;%电磁波角频率
k=w*(u0*e0)^0.5;%波数
sign = -1;%波数前面的正负号
phi_E=0;%初始相位设为 0
phi_H=0;
EE=20;%电场幅度
HH=EE/Yita0;
z=0:0.1:20;%传播方向上的采样点
m0=zeros(size(z));
figure
for t=0:1:300 %为了消除波数与频率之间的数量级带来的影响，时间单位为 ns
Ex=EE*cos(sign*k*z+w*t*1e-9+phi_E); %电场强度值
Hy=HH*cos(sign*k*z+w*t*1e-9+phi_H); %磁场强度值
plot3(z,Ex,m0,'b','LineWidth',2);%绘制电场传播曲线
hold on
plot3(z,m0,Hy,'r','LineWidth',2);%绘制磁场传播曲线
hold off
xlabel('z')
ylabel('Ex')
zlabel('Hy')
title(['平面电磁波传播示意图','t=',num2str(t),'ns'],'fontsize',14)
set(gca,'fontsize',12)
drawnow
frame=getframe(1);%获取当前图像
end

修改上面例子中 MATLAB 程序画出课本例 5.1.1 中电场和磁场在 t=0 时随空间的波形变化,所有参量改成例题例 5.1.1 中的数值，另外修改传播方向上的采样点为 z=0:0.1:10

代码：

u0=1e-6;%自由空间中的磁导率
e0=4e-12;%自由空间中的电介质常数
Yita0=(u0/e0)^0.5;%自由空间中的波阻抗
f=0.1e8;%电磁波的频率
w=2*pi*f;%电磁波角频率
k=w*(u0*e0)^0.5;%波数
sign = -1;%波数前面的正负号
phi_E=0;%初始相位设为 0
phi_H=0;
EE=1;%电场幅度
HH=EE/Yita0;
z=0:0.1:10;%传播方向上的采样点
m0=zeros(size(z));
figure
for t=0:1:300 %为了消除波数与频率之间的数量级带来的影响，时间单位为 ns
Ex=EE*cos(sign*k*z+w*t*1e-9+phi_E); %电场强度值
Hy=HH*cos(sign*k*z+w*t*1e-9+phi_H); %磁场强度值
plot3(z,Ex,m0,'b','LineWidth',2);%绘制电场传播曲线
hold on
plot3(z,m0,Hy,'r','LineWidth',2);%绘制磁场传播曲线
hold off
xlabel('z')
ylabel('Ex')
zlabel('Hy')
title(['平面电磁波传播示意图','t=',num2str(t),'ns'],'fontsize',14)
set(gca,'fontsize',12)
drawnow
frame=getframe(1);%获取当前图像
end

例2：掌握线极化、左旋圆极化、右旋圆极化、椭圆极化的判断

%传输参数
Exm = 12; % x 分量幅值
Eym = 12; % y 分量幅值
Qx = 0; %x 分量初相角
Qy = pi/2; %y 分量初相角 Qy - Qx = 0, pi 时
Emax=max(abs(Exm),abs(Eym))
u0=4*pi*1e-7;%自由空间中的磁导率
e0=1e-9/(36*pi);%自由空间中的电介质常数
w = 2*pi*1e8; % 角频率
k=w*(u0*e0)^0.5;%波数
z0 = 0; % 起始位置
z = 0:0.01:15; % x 轴坐标取样
m0 = zeros(size(z)); % 与 x 取样序列规模相同的 0 序列
N=100;
figure
for t=0:500
Ex = Exm*cos(-k*z+w*t*1e-9+Qx); % 计算 x 方向幅值瞬时序列
Ey = Eym*cos(-k*z+w*t*1e-9+Qy); % 计算 y 方向幅值瞬时序列
subplot(1,2,1);
plot3(z,m0,m0,'black','LineWidth',3); %画参考轴
hold on
plot3(z, Ex, m0,'m','LineWidth', 1.5); % 画 x 轴方向分量
hold on
plot3(z, m0, Ey,'b','LineWidth', 1.1);% 画 y 轴方向分量
hold on
% 和向量 y 坐标为 Y 分量幅值，z 坐标为 X 分量幅值
plot3(z, Ex, Ey,'g','LineWidth', 1.2);
hold off
%轴的设置
xlabel('传播方向 z');
ylabel('电场 Ex');
zlabel('电场 Ey');
title(['平面电磁波传播示意图'],'fontsize',14)
set(gca,'fontsize',12)
drawnow
xx=0:Ex(1)./N:Ex(1);
yy=0:Ey(1)./N:Ey(1);
subplot(1,2,2);
plot(yy,xx,'LineWidth',5)
xlim([-Emax Emax])
ylim([-Emax Emax])
xlabel('电场 Ey');
ylabel('电场 Ex');
drawnow
end

运行结果：

实验结果与分析：
（1）展示程序结果,分析振幅分量相同，相位差为 pi/2 时电场的极化特性。
（2）将例题相位差改为 0，分析极化特性。
（3）将例题相位差改为 pi，分析极化特性。
（4）将例题相位差改为-pi，分析极化特性。
（5）将相位差改为 0，振幅改为 20 和 4 分析极化特性。
（6）将相位差改为-pi/2。
（7）将相位差改为 pi/2,振幅改为 4 和 20 分析极化特性。
（8）将相位差改为-pi/2，振幅改为 4 和 20 分析极化特性。
（9）将相位差改为 pi/2,振幅改为 20 和 4 分析极化特性。
（10）将传播方向改为-z。

（2）：

（3）