目录
1. 霍尔逻辑(Proving Programs Correct)
1.1 警告(Caveats)
1.2 误解(Misconception)
1.3 编程语言(Programming Language)
1.4 程序(Programs)
1.5 证明(Proof)
1.6 霍尔三元组(Hoare Triples)
1.7 逻辑(Logic Refresher)
1.8 推理规则(Inference Rules)
1.9 赋值语句(Assignment Statements)
1.10 赋值规则(Rule of Assignment)
1.11 推论规则(Rule of Consequence)
1.12 结合两个规则(Combining the Two Rules)
2. 赋值规则与最弱前置条件规则 Assignment Rule as Weakest Precondition Rules
2.1 最弱前置条件推理 Weakest Precondition Reasoning
2.2 序列规则 Rule of Sequencing
2.3 Larger Programs
2.3.1 逐步推理
2.3.2 最终证明
2.4 Skip
2.5 条件规则 Conditional Rule
2.5.1 示例:寻找最大值
2.6 迭代规则
2.6.1 迭代的例子:计算阶乘
1. 霍尔逻辑(Proving Programs Correct)
霍尔逻辑是一种理论方法,用于证明程序的正确性,即程序的运行结果符合我们预期的功能和效果。但是,证明程序的正确性并不意味着程序就一定没有错误或bug,还存在一些潜在的问题和误解:
1.1 警告(Caveats)
- 如果证明了程序的正确性,就保证没有错误吗?答案是不确定的,原因如下:
- 错误的规格说明(Incorrect specification):你可能证明了错误的事情。
- 程序与已证明内容不同(Program differs from what was proved):证明总是基于数学模型,而实际的程序可能与模型存在差异。
- 程序执行与理想状态不同(Program's execution differs from ideal):可能由于编译器或硬件错误,硬件故障等导致。
1.2 误解(Misconception)
- 证明过程很困难吗?如果你仔细理解编程,证明过程并不困难。
1.3 编程语言(Programming Language)
这部分介绍了如何在霍尔逻辑中表示程序的基本元素。
-
程序(Procedures)
P := procedure p(v1,...,vn) ^= S- 其中v1, . . .,vn是变量名,p是程序名,S是程序语句。
-
表达式(Expressions)
E := NE | a[NE]NE := n | v | E1+E2 | E1-E2 | E1xE2 | E1/E2 | etc...- 这里,n是一个数字,v是一个变量,a是一个数组变量,NE是一个数字表达式,E是一个表达式。
-
布尔表达式(Booleans)
B := true | false | 反B | E1=E2 | E1 <= E2 | etc. . .- B代表布尔表达式。
-
语句(Statements)
S := skip | v:=E | a[NE] := E | p(E1,...,En) | S1;S2 | if B then S1 else S2 endif | while B do C done- 这里,v是一个变量,a是一个数组变量,p是一个程序名。S代表语句。
通过这些基本元素和结构,我们可以在霍尔逻辑中建立和证明程序的模型。
1.4 程序(Programs)
这部分示例展示了一个阶乘程序FACTORIAL,输入是n,输出是f。主程序调用了FACTORIAL (10,f)。
procedure p1 (v1,...,vm) ^= S1
...
procedure pn (v1,...,vn) ^= Sn
S -> “main” program: -> FACTORIAL (10,f)
procedure FACTORIAL(in n, out f)
f := 1
i := 0
while i /= n do
i:=i+1
f:=f×i
end while
end procedure
FACTORIAL (10,f)
1.5 证明(Proof)
证明程序的正确性是遵循程序的结构,自顶向下。为了证明关于X的某件事,我们需要分析X的内部组件。
1.6 霍尔三元组(Hoare Triples)
霍尔逻辑使用霍尔三元组 {P} S {Q} 来描述程序的行为,其中:
P是前置条件(Precondition);S是程序;Q是后置条件(Postcondition)。
例如,{ x = 2 } x := x + 1 { } 描述的是,在执行 x := x + 1 之前,x 的值是 2。这是最强后置条件的示例。另一个示例是最弱前置条件 { } x := x + 1 { x = 1 },这表示在 x := x + 1 执行后,x 的值应该是 1。
1.7 逻辑(Logic Refresher)
这部分是对逻辑符号的一些基本介绍:
A → B表示“蕴含”,即如果A为真,则B也为真;¬A表示“非”或“否定”,表示A不为真;A ∧ B表示“与”或“合取”,表示A和B都为真;A ∨ B表示“或”或“析取”,表示A或B至少有一个为真;true表示永远为真的命题;false表示永远为假的命题。
1.8 推理规则(Inference Rules)
推理规则用于逻辑推理。以下是一些示例:
- 模态三段论(Modus Ponens):如果
A为真,并且A → B为真,则B为真;

- 公理(Axiom):
true总是为真;

- 结构规则(Structural Rule):如果
A和B都为真,则A ∧ B为真。

1.9 赋值语句(Assignment Statements)
赋值语句是最基本的程序语句。霍尔逻辑为赋值语句提供了一种形式化的表示方法,该表示方法包含前置条件、赋值语句本身和后置条件。例如:
{ x = 2 } x := x + 1 { }表示在执行x := x + 1之前,x的值是2。{ } x := x + 1 { x = 1 }表示在x := x + 1执行后,x的值是1。
1.10 赋值规则(Rule of Assignment)
赋值规则描述了在给变量 x 赋值表达式 E 后,前置条件 P 如何变为后置条件。规则为:
![]()
( ) / {P[E/x]} x := E {P}
例如,为了证明 { } x := x + 1 { x = 1 },我们需要找到满足 {P[E/x]} x := E {P} 的 P。在这个例子中,P 是 x = 1,E 是 x + 1,所以 P[E/x] 是 x + 1 = 1,也就是 x = 0。所以,我们有 { x = 0 } x := x + 1 { x = 1 }。
1.11 推论规则(Rule of Consequence)
推论规则描述了如何通过已知的霍尔三元组 {P}S{Q} 得到新的霍尔三元组 {P'}S{Q'}。规则为:
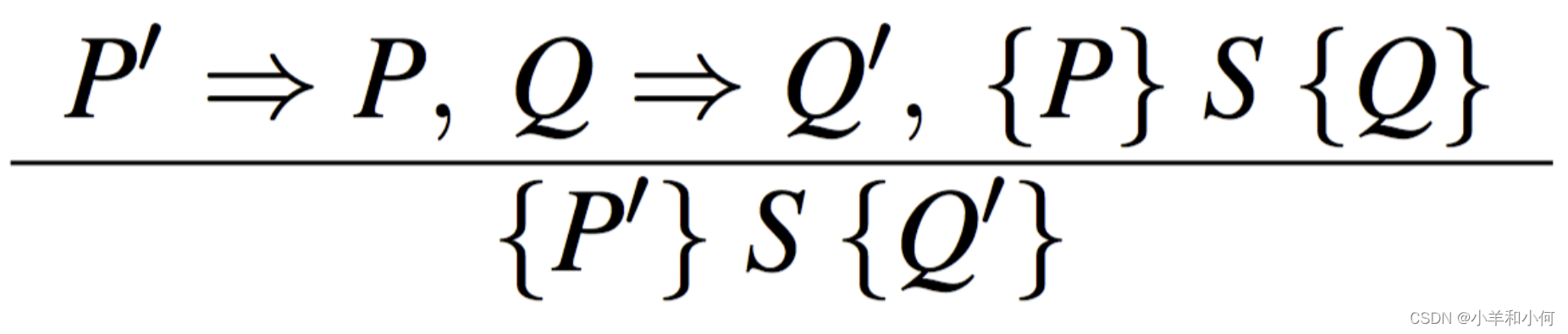
(p' => P, Q => Q', {P}S{Q}) / ({P'}S{Q'})
例如,假设我们已经证明了 { x = 0 } x := x + 1 { x = 1 },那么我们可以通过推论规则得到 { x = 0 } x := x + 1 { x > 0 },因为 x = 1 蕴含 x > 0。
1.12 结合两个规则(Combining the Two Rules)
这部分展示了如何将赋值规则和推论规则结合起来使用。首先,使用推论规则来扩大前置条件,然后使用赋值规则。这是一个通用的模式。例如,假设我们希望证明 { x = 0 } x := x + 1 { x > 0 },我们可以先应用推论规则,然后再应用赋值规则:


(x = 0 → ?P { ?P } x := x + 1 { x > 0 }) / ({ x = 0 } x := x + 1 { x > 0 })

( ( ) / (x = 0 → x + 1 > 0) ( ) / ({ x + 1 > 0 } x := x + 1 { x > 0 }) ) / ({ x = 0 } x := x + 1 { x > 0 })
此模式的推导过程说明了在程序验证中,推论规则和赋值规则是如何配合使用的。
2. 赋值规则与最弱前置条件规则 Assignment Rule as Weakest Precondition Rules
{ } x := E {P}
这个规则描述了给定某个具体后置条件P时,如何计算保证P之后成立的最弱前置条件。如果我们有一个形如x := E的赋值语句,并且我们知道执行这个赋值语句之后必须满足某个条件P,那么我们可以通过计算最弱前置条件来确定在执行这个赋值语句之前必须满足的条件。对于其他类型的语句(例如if, while, skip, sequencing等),我们将看到同样形式的规则,这使得我们可以从一个具体的后置条件计算最弱前置条件。
2.1 最弱前置条件推理 Weakest Precondition Reasoning
给定具体的前置条件P'和Q以及一些程序S,要证明:
{P′} S {Q}
首先应用后果规则来概括前提条件,给出两个要证明的目标:
{?P} S {Q}
然后,通过应用最弱前置条件规则来计算?P是什么
P′ ⟹ ?P
一旦计算出?P,最后检查此蕴含关系是否成立。
这个过程描述了给定具体的前置条件P'和后置条件Q以及一些程序S时,如何证明形如{P′} S {Q}的命题。首先,我们应用 consequence rule 来将前置条件泛化,这给出了我们需要证明的两个目标:{?P} S {Q} 和 P′ ⟹ ?P。然后,我们通过应用最弱前置条件规则计算出 ?P 是什么。一旦 ?P 被计算出来,最后检查这个蕴含关系是否成立。
2.2 序列规则 Rule of Sequencing
序列规则描述了如何通过两个霍尔三元组 {P} S1 {R} 和 {R} S2 {Q} 推导出新的霍尔三元组 {P} S1; S2 {Q}:
({P} S1 {R}, {R} S2 {Q}) / {P} S1; S2 {Q}
例如,为了证明 {x = 0} x := x+1; x := x+1 {x=2},我们可以先应用后果规则,然后应用序列规则和赋值规则。最后我们需要检查 x = 0 → x+2=2 是否成立,这就是最弱前置条件推理。

Proof:




2.3 Larger Programs

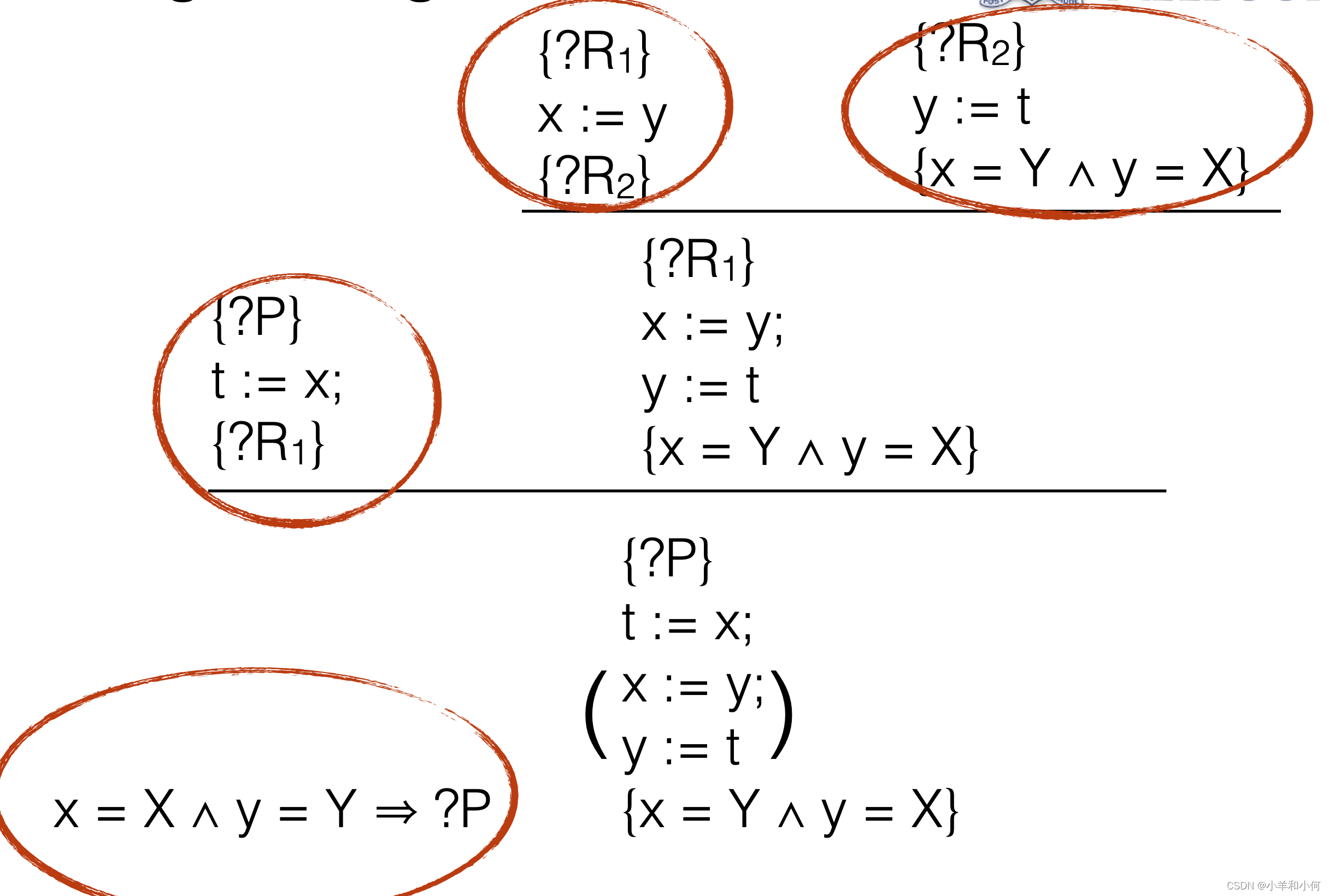


如何使用之前讨论过的规则(后果规则,序列规则和赋值规则)来推理有关更大程序的性质。考虑下面的程序,它将x和y的值交换:
{x = X ∧ y = Y}
t := x;
x := y;
y := t
{x = Y ∧ y = X}
我们将这个要证明的性质写成形式化的形式:{x = X ∧ y = Y} t := x; x := y; y := t {x = Y ∧ y = X}。
要使用序列规则推理此程序,我们需要考虑程序中每个赋值语句的前置条件和后置条件。
2.3.1 逐步推理
推理过程从程序的最后一步开始(这是因为后置条件与最后一步最直接相关),然后反向工作到程序的开始。每个步骤都有一个前置条件?P和一个后置条件?R。
首先,我们将原始的程序拆分为三个更简单的步骤:t := x;、x := y; 和 y := t;。然后,我们为每个步骤计算其最弱前置条件,这些最弱前置条件就是在执行每个步骤之前必须满足的条件。计算过程使用了之前提到的赋值规则:{P[E/x]} x := E {P},其中 P[E/x] 表示将 P 中的 x 替换为 E。
例如,第一步的后置条件是{x = Y ∧ y = X},通过赋值规则我们可以计算其最弱前置条件为{x = Y ∧ t = X}。这意味着在执行 y := t 之前,我们需要确保 x 的值是 Y,t 的值是 X。
首先关注的是最后的部分
{?R2}
y := t
{x = Y ∧ y = X}
根据{P[E/x]} x := E {P}变成:
{(x = Y ∧ y = X) [t/y]}
y := t
{x = Y ∧ y = X}
变成:
{x = Y ∧ t= X}
y := t
{x = Y ∧ y = X}
然后我们会将这个新计算的前置条件作为下一步(x := y)的后置条件,再次应用赋值规则,计算其最弱前置条件为{y = Y ∧ t = X}。
接下来是证明
{?R1}
x := y;
{x = Y ∧ t= X}
推导:
{(x = Y ∧ t = X) [y/x]}
x := y;
{x = Y ∧ t= X}
变成:
{y = Y ∧ t = X}
x := y;
{x = Y ∧ t= X}我们继续这个过程,将{y = Y ∧ t = X}作为下一步(t := x)的后置条件,再次应用赋值规则,计算其最弱前置条件为{y = Y ∧ x = X}。
接下来到了:
{?P}
t := x;
{y = Y ∧ t = X}
推导:
{(x = Y ∧ t = X) [x/t]}
t := x;
{y = Y ∧ t = X}
变成:
{y = Y ∧ x = X}
t := x;
{y = Y ∧ t = X}2.3.2 最终证明
最后,我们需要检查初始的前置条件{x = X ∧ y = Y}是否蕴含最初计算的前置条件{y = Y ∧ x = X}。在这个例子中,这是正确的,因为它们都表达了相同的事实(只是顺序不同)。所以,我们成功地证明了这个程序的性质:它将x和y的值交换。换句话说:
在最后一步,我们使用了逻辑等价性,即 x = X ∧ y = Y 是等价于 y = Y ∧ x = X 的,这意味着如果 x = X 和 y = Y 都为真,那么 y = Y 和 x = X 也都为真,反之亦然。因此,我们证明了 {x = X ∧ y = Y} t := x; x := y; y := t {x = Y ∧ y = X} 是正确的。
2.4 Skip

skip 是一个在程序中不执行任何操作的语句。在 Hoare 逻辑中,我们可以写作 {P} skip {P},这意味着在任何条件 P 下执行 skip,结束后的条件依然是 P。因为 skip 并不改变任何变量的值,所以前后的条件保持一致。
2.5 条件规则 Conditional Rule
![]()
条件语句的形式化规则可以写作 {P1} S1 {Q}, {P2} S2 {Q} / {(B => P1) ∧ (¬B => P2)} if B then S1 else S2 endif {Q}。这个规则表明,在执行 if 语句之前的条件应当是当条件 B 成立时 P1 成立,当条件 B 不成立时 P2 成立。然后分别对 S1 和 S2 应用对应的前提条件 P1 和 P2,在两种情况下的后置条件都是 Q。
换句话说,给定后置条件Q,如果我们知道在B为真的情况下执行S1可以达到Q,并且在B为假的情况下执行S2也可以达到Q,那么整个if语句在前置条件为B蕴含P1并且非B蕴含P2的情况下可以保证Q。
2.5.1 示例:寻找最大值
考虑这样一个简单的程序,它的目的是使得r等于x和y中的最大值:
{true}
if x > y then
r := x;
else
r := y;
endif
{r ≥ x ∧ r ≥ y}
首先,对于 if 语句的两个分支,我们分别计算最弱前提条件。
Apply consequence rule first (p' => P, Q => Q', {P}S{Q}) / ({P'}S{Q'})
{ }
if x > y then
r := x;
else
r := y;
endif
{r ≥ x ∧ r ≥ y}({P1} S1 {Q}, {P2} S2 {Q}) / ({(B => P1) ∧ (¬B => P2)} if B then S1 else S2 endif {Q})
{true}
{?P}
if x > y then
r := x;
else
r := y;
endif
{r ≥ x ∧ r ≥ y}( ) / ({P[E/x]} x := E{P})
{true}
{(x>y → ?P1) ∧ (x≤y → ?P2)}
if x > y then
{?P1}
r := x;
{r ≥ x ∧ r ≥ y}
else
{?P2}
r := y;
{r ≥ x ∧ r ≥ y}
endif
{r ≥ x ∧ r ≥ y}
{true}
{(x>y → x ≥ x ∧ x ≥ y) ∧ (x≤y → y ≥ x ∧ y ≥ y)}
if x > y then
{x ≥ x ∧ x ≥ y}
r := x;
{r ≥ x ∧ r ≥ y}
else
{y ≥ x ∧ y ≥ y}
r := y;
{r ≥ x ∧ r ≥ y}
endif
{r ≥ x ∧ r ≥ y}{true}
{(x>y → x ≥ x ∧ x ≥ y) ∧ (x≤y → y ≥ x ∧ y ≥ y)}
if x > y then
{x ≥ x ∧ x ≥ y}
r := x;
{r ≥ x ∧ r ≥ y}
else
{y ≥ x ∧ y ≥ y}
r := y;
{r ≥ x ∧ r ≥ y}
endif
{r ≥ x ∧ r ≥ y}r := x; 的最弱前提条件是 x ≥ x ∧ x ≥ y,
r := y; 的最弱前提条件是 y ≥ x ∧ y ≥ y。
所以,整个 if 语句的最弱前提条件是 (x > y → x ≥ x ∧ x ≥ y) ∧ (x ≤ y → y ≥ x ∧ y ≥ y)。这个条件是一个逻辑表达式,表示 x 大于 y 时,x 应该大于等于 x 和 y,而当 x 小于等于 y 时,y 应该大于等于 x 和 y。
在得到每个分支的最弱前提条件之后,我们只需要验证这个前提条件是满足的,就能证明整个程序的正确性。
在这个例子中,前提条件 (x > y → x ≥ x ∧ x ≥ y) ∧ (x ≤ y → y ≥ x ∧ y ≥ y) 是满足的,因为对于任意的 x 和 y,x 总是大于等于 x,y 总是大于等于 y,所以无论 x 和 y 的大小关系如何,r 的值总是大于等于 x 和 y。
所以,我们成功证明了 {true} if x > y then r := x; else r := y; endif {r ≥ x ∧ r ≥ y} 是正确的。
2.6 迭代规则
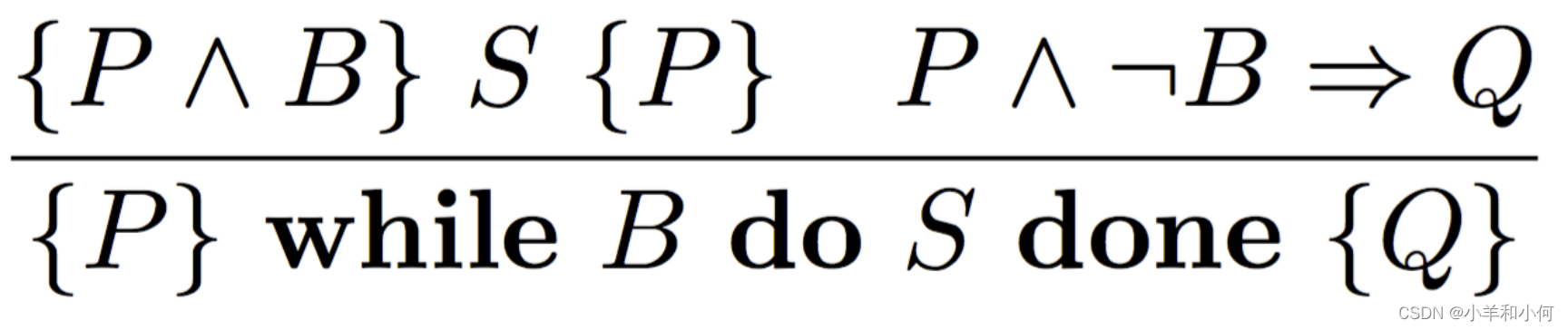
迭代规则是用于处理 while 循环语句的形式化规则。规则为:({P ∧ B} S {P} P ∧ ¬B => Q) / ({P} while B do S done {Q})。
这里的
P代表循环不变量(loop invariant)。B是循环条件,S是循环体。Q是我们希望在循环结束后达成的后置条件。
这个规则表示的是,在每次循环开始时,如果循环条件 B 成立,且循环不变量 P 满足,那么在执行完循环体 S 后,循环不变量 P 仍然保持。如果循环条件 B 不成立,那么 P 必须能推出我们期望的后置条件 Q。
2.6.1 迭代的例子:计算阶乘
接下来是一个例子,程序如下,其目标是计算N的阶乘并将结果存储在n中:
{true}
i := 0;
n := 1;
while i ≠ N do
i := i + 1
n := i * n;
done
{ }{true}
{?Q}
i := 0;
{?P}
n := 1;
{?I}
while i ≠ N do
i := i + 1
n := i * n;
done
{n = N!}{true}
i := 0;
n := 1;
while i ≠ N do
i := i + 1;
n := i * n;
done
{n = N!}
我们希望在循环结束后,n 的值等于 N!,即 N 的阶乘。在此过程中,我们尝试找到一个适合的循环不变量 P,使得我们能够应用迭代规则来证明这个程序的正确性。
首先,我们假设循环不变量 I 为 n = i!,表示在每次循环开始时,n 的值等于 i 的阶乘。
然后我们需要检查在执行循环体之后,这个循环不变量是否仍然保持。
{?I}
while i ≠ N do
i := i + 1
n := i * n;
done
{n = N!}这里的P是我们假设的循环不变量 {?I},B是循环条件i ≠ N,Q是{n = N!}
根据({P ∧ B} S {P} P ∧ ¬B => Q) / ({P} while B do S done {Q})
{?I} -- P
while i ≠ N do
{?I ∧ i ≠ N} -- 这里是P∧B
i := i + 1
n := i * n;
{?I} -- P
done
{n = N!} -- B
?I ∧ i = N -> n = N!Let ?I be: n = i!{n = i!}
while i ≠ N do
{n = i! ∧ i ≠ N}
i := i + 1
n := i * n;
{n = i!}
done
{n = N!}n = i! ∧ i = N → n = N!在 i := i + 1 执行之后,我们需要 n = (i+1)!。由于下一步是 n := i * n,我们希望能够在此步之前满足 (i+1)*n = (i+1)!。通过替换前面的循环不变量,我们可以得到 i*n = i!。这表示,在执行 n := i * n 之后,n 的值应该等于 (i+1)!,这也是我们希望的结果。
{n = i! ∧ i ≠ N}
i := i + 1
n := i * n;
{n = i!}
{n = i! ∧ i ≠ N}
{?R2}
i := i + 1
n := i * n;
{n = i!}赋值规则 ( ) / ({P[E/x]} x := E {P})
{n = i! ∧ i ≠ N}
{?R2}
i := i + 1
{?R}
n := i * n;
{n = i!}{n = i! ∧ i ≠ N}
{?R2}
i := i + 1
{(n = i!)[i * n / n]}
n := i * n;
{n = i!}首先,我们考虑的是n := i * n; 对于这个表达式我们使用赋值规则。这里的P是 n = i!,x是n := i * n,{?R}是将P中的n换成i * n,即{(n = i!)[i * n / n]} ,意思为在n = i!中,使用i * n替换掉n。
{n = i! ∧ i ≠ N}
{?R2}
i := i + 1
{i*n = i!}
n := i * n;
{n = i!}其次,我们考虑 i := i + 1 这个语句,我们希望找到一个 R2 ,使得 {n = i! ∧ i ≠ N} i := i + 1 {R2} 成立。根据赋值规则,我们找到 R2 = (n = i!)[i+1/i],也就是(i+1)*n = (i+1)!。
{n = i! ∧ i ≠ N}
{(i*n = i!)[i+1/i]}
i := i + 1
{i*n = i!}
n := i * n;
{n = i!}{n = i! ∧ i ≠ N}
{(i+1)*n = (i+1)!}
i := i + 1
{i*n = i!}
n := i * n;
{n = i!}然后,我们需要证明 n = i! ∧ i ≠ N → (i+1)*n = (i+1)! 成立,也就是说,如果当前 n 等于 i 的阶乘,且 i 不等于 N,那么 (i+1)*n 一定等于 (i+1)!。这个式子在数学上是成立的,因为 (i+1)*n 在这里等于 (i+1)*i!,而 (i+1)*i! 正好等于 (i+1)!。
n = i! ∧ i ≠ N -> ((i+1)*n = (i+1)!)这里的赋值规则指的是 Hoare 逻辑中的赋值规则,形式如下:
( ) / ({P[E/x]} x := E {P})这个规则是说,如果在赋值语句
x := E之后,程序的状态满足某个条件P,那么在执行赋值语句之前,程序的状态必须满足把E代入x的P。换句话说,我们可以把P中所有的x替换为E,得到赋值语句前的条件P[E/x]。
最后,我们需要确认当循环条件不成立时,即 i ≠ N 为假,也就是 i = N 时,循环不变量 n = i! 能够推出后置条件 n = N!。显然这个条件是满足的。
经过以上的推理,我们证明了这个程序是正确的,即这个程序能够计算 N!。在程序结束时,n 的值等于 N!。
这个过程是用 Hoare 逻辑进行程序正确性证明的典型例子,显示了如何找到合适的循环不变量,以及如何通过形式化的推理规则进行程序的正确性证明。
{true}
{?Q}
i := 0;
{?P}
n := 1;
{n = i!}
while i ≠ N do
{n = i! ∧ i ≠ N}
{(i+1)*n = (i+1)!}
i := i + 1
{i*n = i!}
n := i * n;
{n = i!}
done
{n = N!}还是因为赋值表达式,{?P} 就是 {(n = i!)[1/n]}
{true}
{?Q}
i := 0;
{(n = i!)[1/n]}
n := 1;
{n = i!}
while i ≠ N do
{n = i! ∧ i ≠ N}
{(i+1)*n = (i+1)!}
i := i + 1
{i*n = i!}
n := i * n;
{n = i!}
done
{n = N!}{true}
{?Q}
i := 0;
{1 = i!}
n := 1;
{n = i!}
while i ≠ N do
{n = i! ∧ i ≠ N}
{(i+1)*n = (i+1)!}
i := i + 1
{i*n = i!}
n := i * n;
{n = i!}
done
{n = N!}同理,因为赋值表达式,{?Q} 就是 {(1 = i!)[0/i]}
{true}
{(1 = i!)[0/i]}
i := 0;
{1 = i!}
n := 1;
{n = i!}
while i ≠ N do
{n = i! ∧ i ≠ N}
{(i+1)*n = (i+1)!}
i := i + 1
{i*n = i!}
n := i * n;
{n = i!}
done
{n = N!}{true}
{1 = 0!}
i := 0;
{1 = i!}
n := 1;
{n = i!}
while i ≠ N do
{n = i! ∧ i ≠ N}
{(i+1)*n = (i+1)!}
i := i + 1
{i*n = i!}
n := i * n;
{n = i!}
done
{n = N!}Does true -> 1 = 0! ? YES!完成!