系列文章目录

机器学习神经网络——Adaboost分离器算法

机器学习之SVM分类器介绍——核函数、SVM分类器的使用

机器学习的一些常见算法介绍【线性回归，岭回归，套索回归，弹性网络】

文章目录

系列文章目录

前言

一、GBDT(Gradient Boosting Decision Tree) 梯度提升决策树简介

1.1、集成学习

1.2、Boosting

1.3、AdaBoost

1.4、Gradient Boosting

1.5、决策树与CART

二、GBDT算法的案例解读

2.1、使用梯度提升算法和决策树分类器对手写数字数据进行对比分析

2.2、GBDT算法参数的介绍

2.3、GBDT适用范围

总结

前言

本文主要介绍GBDT算法，以及使用梯度提升算法和决策树分类器对手写数字数据进行对比分析的案例介绍

一、GBDT(Gradient Boosting Decision Tree) 梯度提升决策树简介

DT－Decision Tree决策树，GB是Gradient Boosting，是一种学习策略，GBDT的含义就是用Gradient Boosting的策略训练出来的DT模型

在前几年深度学习还没有大行其道之前，GBDT在各种竞赛是大放异彩。一是效果确实挺不错。二是即可以用于分类也可以用于回归。三是可以筛选特征

1.1、集成学习

集成学习就是将多个弱的学习器结合起来组成一个强的学习器。
这就涉及到，先产生一组‘个体学习器’，再用一个策略将它们结合起来。

个体学习器可以选择：决策树，神经网络。

集成时可以所有个体学习器属于同一类算法：全是决策树，或全是神经网络；也可以来自不同的算法。

结合策略：例如分类问题，可以用投票法，少数服从多数。
之所以用这种集成的思想，是因为单独用一个算法时，效果往往不容易达到很好，但如果多个个体算法结合在一起，取长补短，整体效果就会比单独一个要强。

当然集成并不是不管怎么选择学习器，怎么组合都一定会获得更好的效果，最好的情况是，每个学习器都不是特别差，并且要具有一定的多样性，否则可能集成后的会没有效果，或者起负作用。

这就是集成学习的一个核心问题：如何生成准确性又不是很差，并且还能保证多样性的个体学习器呢

目前主要有两种生成方式：

Boosting：个体学习器间存在强依赖关系，必须串行生成。
Bagging，随机森林：个体之间不存在强依赖关系，可并行生成。

1.2、Boosting

Boosting 的思想,三个臭皮匠顶一个诸葛亮:

给定初始训练数据，由此训练出第一个基学习器；
根据基学习器的表现对样本进行调整，在之前学习器做错的样本上投入更多关注；
用调整后的样本，训练下一个基学习器；
重复上述过程 T 次，将 T 个学习器加权结合。
简单讲，就是每次训练单个弱学习器时，都将上一次分错的数据权重提高一点再进行当前单个弱学习器的学习。这样越往后执行，训练出的单个弱学习器就会越在意那些容易分错（权重高）的点。当执行 M 次后，通过加权求和的方式组合成一个最终的学习器。

Boosting模型可以抽象为一个前向加法模型（additive model）:
根据 Boosting 的定义，它有三个基本要素：

基学习器
组合方式
目标函数

1.3、AdaBoost

Boosting 的代表是 Adaboost。

• 第 1 行，初始化样本权重分布，此时每个数据的权重是一样的，所以是 1/m；
以分类问题为例，最初令每个样本的权重都相等，对于第 t 次迭代操作，我们就根据这些权重来选取样本点，进而训练分类器 C_t。
• 第 2 行，进入 for 循环 T 次，即基学习器的个数为 T 个；
• 第 3 行，根据具有当前权重分布 D_t 的数据集，学习出 h_t；
前一个分类器分错的样本会被用来训练下一个分类器。
h_t 是分量分类器 C_t 给出的对任一样本点 xi 的标记（+1或-1），h_t(xi) = yi 时，样本被正确分类。
• 第 4 行，计算当前学习器的误差；
• 第 5 行，如果误差大于 0.5，就停止；
AdaBoost 方法中使用的分类器可能很弱（比如出现很大错误率），但只要它的分类效果比随机好一点（比如两类问题分类错误率略小于0.5），就能够改善最终得到的模型。
• 第 6 行，计算当前学习器的权重 α_t；
权值是关于误差的表达式，当下一次分类器再次错分这些点之后，会提高整体的错误率，这样就导致分类器权值变小，进而导致这个分类器在最终的混合分类器中的权值变小，也就是说，Adaboost算法让正确率高的分类器占整体的权值更高，让正确率低的分类器权值更低，从而提高最终分类器的正确率。
• 第 7 行，得到下一时刻的权重分布 D_t＋1.
如果某个样本点已经被准确地分类，那么在构造下一个训练集中，它被选中的概率就被降低；相反，如果某个样本点没有被准确地分类，那么它的权重就得到提高。通过这样的方式，AdaBoost 方法能“聚焦于”那些较难分（更富信息）的样本上。

此算法的案例可以参考本篇博客

机器学习神经网络——Adaboost分离器算法

1.4、Gradient Boosting

AdaBoost每一轮基学习器训练过后都会更新样本权重，再训练下一个学习器，最后将所有的基学习器加权组合。AdaBoost使用的是指数损失，这个损失函数的缺点是对于异常点非常敏感，因而通常在噪音比较多的数据集上表现不佳。Gradient Boosting在这方面进行了改进，使得可以使用任何损失函数 (只要损失函数是连续可导的)，这样一些比较robust的损失函数就能得以应用，使模型抗噪音能力更强。
和Adaboost不同，Gradient Boosting 在迭代的时候选择梯度下降的方向来保证最后的结果最好。
算法将负梯度作为残差值来学习基本模型h(x).

1.5、决策树与CART

1976年-1986年，J.R.Quinlan给出ID3算法原型并进行了总结，确定了决策树学习的理论。这可以看做是决策树算法的起点。1993，Quinlan将ID3算法改进成C4.5算法，称为机器学习的十大算法之一。ID3算法的另一个分支是CART(Classification adn Regression Tree, 分类回归决策树)，用于预测。这样，决策树理论完全覆盖了机器学习中的分类和回归两个领域。

决策树
决策树(decision tree)一般都是自上而下的来生成的。每个决策或事件（即自然状态）都可能引出两个或多个事件，导致不同的结果，把这种决策分支画成图形很像一棵树的枝干，故称决策树。

决策树利用如下图所示的树结构进行决策，每一个非叶子节点是一个判断条件，每一个叶子节点是结论。从跟节点开始，经过多次判断得出结论。

决策树的构建是数据逐步分裂的过程，构建的步骤如下:

步骤1：将所有的数据看成是一个节点，进入步骤2；
步骤2：从所有的数据特征中挑选一个数据特征对节点进行分割，进入步骤3；
步骤3：生成若干孩子节点，对每一个孩子节点进行判断，如果满足停止分裂的条件，进入步骤4；否则，进入步骤2；
步骤4：设置该节点是子节点，其输出的结果为该节点数量占比最大的类别。

从上述步骤可以看出，决策生成过程中有三个重要的问题：

（1）数据如何分割
（2）如何选择分裂的属性
（3）什么时候停止分裂

决策树（decision tree）算法基于特征属性进行分类，其主要的优点：模型具有可读性，计算量小，分类速度快。

二、GBDT算法的案例解读

2.1、使用梯度提升算法和决策树分类器对手写数字数据进行对比分析

#使用梯度提升算法和决策树分类器对手写数字数据进行对比分析
import numpy as np
#导入sklearn内置数据集 
from sklearn.datasets import load_digits
#导入手写数字数据
digits = load_digits()
#以图片形式显示前100号手写数字
import matplotlib.pyplot as plt
plt.figure(1, figsize=(3.5,3.5),facecolor='white') 
for i in range(10): 
    for j in range(10):
        ax= plt.subplot(10,10,10*i+j+1)
        #设置子图的位置
        ax.set_xticks([])
        #隐藏横坐标
        #隐藏纵坐标
        ax.set_yticks([])
        plt.imshow(digits.images[9*i+j],cmap=plt.cm.gray_r,interpolation="nearest")
plt.show()
#导入sklearn中的模型验证类 
from sklearn.model_selection import train_test_split
#使用train test_split函数自动分割训练数据集和测试数据集
x_train,x_test,y_train,y_test = train_test_split(digits.data,digits.target,test_size=0.3)
#导入sklearn模块中的决策树分类器类 
from sklearn.tree import DecisionTreeClassifier
#定义一个决策树分类器对象
dtc = DecisionTreeClassifier()
dtc.fit(x_train,y_train)
#导入sklearn模块中的梯度提升分类器类 
from sklearn.ensemble import GradientBoostingClassifier
#定义一个梯度提升决策树分类器对象
gbc = GradientBoostingClassifier(n_estimators=30,learning_rate=0.1)
gbc.fit(x_train,y_train)
print("单棵决策树在训练集上的性能：%.3f"%dtc.score(x_train,y_train))
print("单棵决策树在测试集上的性能：%.3f"%dtc.score(x_test,y_test))
print("GBDT(T-30)在训练集上的性能：%.3f"%gbc.score(x_train,y_train))
print("GBDT(T-30)在测试集上的性能：%.3f"%gbc.score(x_test,y_test))
#观察弱分类器数量对分类准确度的影响
#弱分类器的最大值
T_max =39
gbc_train_scores=[] 
gbc_test_scores=[] 
for i in range(1,T_max+1):
    gbc = GradientBoostingClassifier(n_estimators=i,learning_rate=0.1)
    gbc.fit(x_train,y_train)
    gbc_train_scores.append(gbc.score(x_train,y_train))
    gbc_test_scores.append(gbc.score(x_test,y_test))
#绘制测试结果
import matplotlib.pyplot as plt
#解决图形中的中文显示乱码
plt.rcParams['font.sans-serif']=['SimHei']
plt.matplotlib.rcParams['axes.unicode_minus']=False 
plt.figure()
#解决图形中的坐标轴负号显示问题
plt.plot(range(1,T_max+1),gbc_train_scores,color='r',label='训练集')
plt.plot(range(1,T_max+1),gbc_test_scores,color='g',label='测试集')
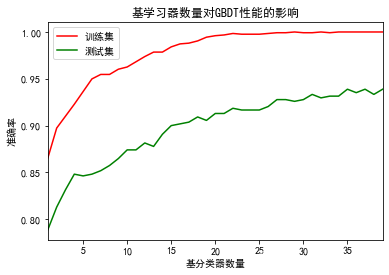
plt.title("基学习器数量对GBDT性能的影响")
plt.xlabel("基分类器数量")
plt.ylabel("准确率")
plt.xlim(1,T_max)
plt.legend()
plt.show()

运行结果：

单棵决策树在训练集上的性能：1.000
单棵决策树在测试集上的性能：0.822
GBDT(T-30)在训练集上的性能：0.999
GBDT(T-30)在测试集上的性能：0.928

案例二

# 导入GBDT分类器模型
from sklearn.ensemble import GradientBoostingClassifier
# 定义一个GBDT分类器模型，设置参数
gbdt = GradientBoostingClassifier(n_estimators=100, learning_rate=0.1, max_depth=3)
# 训练模型
gbdt.fit(X_train, y_train)
# 使用训练好的模型进行预测
y_pred = gbdt.predict(X_test)
# 输出预测结果
print(y_pred)

第一行导入了sklearn库中的GBDT分类器模型。

第二行定义了一个GBDT分类器模型，其中n_estimators表示迭代次数，learning_rate表示学习率，max_depth表示决策树的最大深度。

第三行使用训练数据集进行模型训练。

第四行使用训练好的模型对测试数据集进行预测。

第五行输出预测结果。

案例三

# 导入GBDT分类器模型
from sklearn.ensemble import GradientBoostingClassifier
# 定义一个GBDT分类器模型，设置参数
gbdt = GradientBoostingClassifier(n_estimators=100, learning_rate=0.1, max_depth=3, min_samples_split=2, min_samples_leaf=1, max_features=None)
# 训练模型
gbdt.fit(X_train, y_train)
# 使用训练好的模型进行预测
y_pred = gbdt.predict(X_test)
# 输出预测结果
print(y_pred)

在这个例子中，我们使用了n_estimators=100进行了100次迭代，使用了learning_rate=0.1来调整每个决策树的权重，使用了max_depth=3限制了每个决策树的最大深度，使用了min_samples_split=2和min_samples_leaf=1来限制了节点和叶子节点的最小样本数，使用了max_features=None考虑了所有特征。