C++数据结构
线性顺序表(数组)
线性顺序表(链表)
Python风格双向链表的实现
散列表简单实现(hash表)
栈和队列的应用
二叉树之一(数组存储)
二叉树之二(二叉搜索树)
二叉树之三(二叉搜索树扩展)
图结构入门
图结构入门
- C++数据结构
- 前言
- 一、图是什么?
- 二、图的存储(二维数组)
- 三、图的存储(邻接链表)
- 总结
前言
前面系列文章介绍了线性结构和树形结构,线性结构的前驱与后续非常清晰,很明确的一对一的关系。树形结构是层次分明的结构,同时树形结构的父节点可以有一个或多个(二叉树为两个)子节点,叶子节点没有子节点,这是一种一对多的关系。而图结构更加复杂,是多对多的关系,这种结构在现实生活中应用很广泛,比如公交线路图,计算机的网络结构等等。
一、图是什么?
我们还是先用数学来解释一下,图可以认为是点和边的集合。设存在集合V(n>0,n表示顶点的数量)、集合E(表示点与点之间的关系),那么图就是G={V, E}。如下图左,点与点之间的关系没有方向,我们称之为无向图。如下图右,点与点之间是有方向的,表示只能从箭头方向到达另一个点,这种称为有向图。
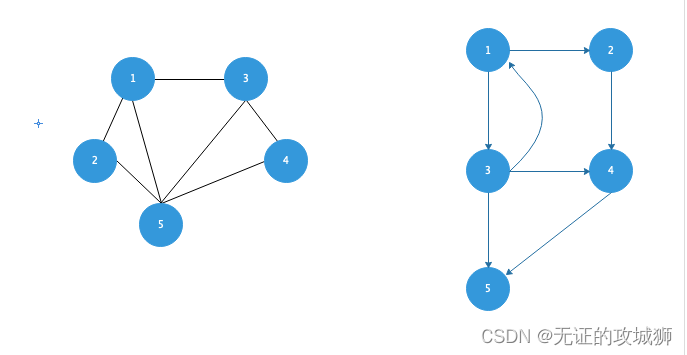
- 图也有度的概念,度表示一个点连接了几条边。
- 路径,表示二个点之间有连接,如上两图中1点和2点之间都有直接连接线,称之为存在直接路径,而1和5之间也都可以到达,它们之间也存在路径。因为右图是有方向的,右图的2到1之间在规则内无法从2到达1,则说明右图不存在从2到1的路径。
- 在无向图中,如果所有点之间都存在路径,我们称之为连通图。如上图左就是连通图。
- 特别的在有向图中,如果所有点之间都存在路径,称之为强连通图。上图右不是强连通图。
- 如果图中只有部分点之间是连通的,则连通的这部分称为连通子图。可以表示为G1={V1, E1 } ,G1⊆G
二、图的存储(二维数组)
树形结构有数组和链表的存储方式,图也是一样的。用数组的方式存储,往往采用二维数组,以数组下标表示二个点,以值0表示不存路径,以1表示存在路径。如上左图可以表示为:S=
{ {0,1,1,0,1} //代表点1与各点的关系
, {1,0,0,0,1} //代表点2与各点的关系,下同
, {1,0,0,1,1}
, {0,0,1,0,1}
, {1,1,1,1,0} }
- 如上,
S[i][j]给示了二个点间的关系。i、j 之间是否存在直接路径就用0、1表示。 - 上面的点1和点1本身之间标注了0,如果标注1,表示这里存在回环,或称环、回路。
- 在抽像表示中,点和点之间的边往往存在不同的权重,比如用于表示路网时,路的距离是不同的,那么我们可以把存在直接路径的边记为权重值,用于表示路网中不同路的距离。也就是不用1表示它们之间存在直接路径,而直接标注路径的距离。
好了,描述得这么清晰,至于写一个 class 来对这个数组进行增、删、改、查就太没必要了,以后用到的时候再写。
三、图的存储(邻接链表)
从上面的数组存储中,我们可以看出,这个存储方式和二叉树的数组存储方式一样存在问题。对于很多点,且点之间联系并不紧密的情况太浪费空间。比如我们要表示全国14亿人口之间的亲戚关系,那这个14亿行,14亿列的数组中13.9999…亿都是0。虽然现在内存不值钱,也不能这么整是吧。
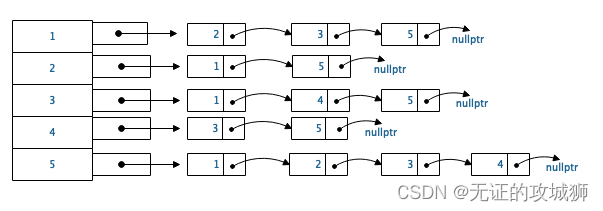
所以我们又想到链表了,我们用一个数组存储所有的点。以数组的下标表示节点号,存储链表的头节点指针。
如果是加权图,我们就要为顶点单独设计一个节点,以便增加权重、链表指针等存储。如果是有向图存储也是一样的,只是没有反方向的边。要根据实际灵活运用了。
总结
图的基本结构并不复杂,构建起来不比二叉树难,要是有人看,我继续写这个系列文章后续的算法部分肯定会有图相关的内容。