所需先验知识(没有也无大碍,只是了解的话会对D*的理解有帮助):A*算法/ Dijkstra算法
何为D*算法
Dijkstra算法是无启发的寻找图中两节点的最短连接路径的算法,A*算法则是在Dijkstra算法的基础上加入了启发函数h(x),以引导Dijkstra算法搜索过程中的搜索方向,让无必要搜索尽可能的少,从而提升找到最优解速度。这两者都可应用于机器人的离线路径规划问题,即已知环境地图,已知起点终点,要求寻找一条路径使机器人能从起点运动到终点。

但是上述两个算法在实际应用中会出现问题:机器人所拥有的地图不一定是最新的地图,或者说,机器人拥有的地图上明明是可以行走的地方,但是实际运行时却可能不能走,因为有可能出现有人突然在地上放了个东西,或者桌子被挪动了,或者单纯的有一个行人在机人运行时路过或挡在机器人的面前。

碰到这样的问题,比如机器人沿着预定路径走到A点时,发现在预先规划的路径上,下一个应该走的点被障碍物挡住了,这种情况时,最简单的想法就是让机器人停下来,然后重新更新这个障碍物信息,并重新运行一次Dijkstra算法 / A*算法,这样就能重新找到一条路。
但是这样子做会带来一个问题:重复计算。假如如下图所示新的障碍物仅仅只是挡住了一点点,机器人完全可以小绕一下绕开这个障碍物,然后后面的路径仍然按照之前规划的走。可是重复运行Dijkstra算法 / A*算法时却把后面完全一样的路径重新又计算了一遍
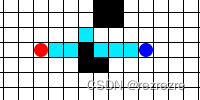
D*算法的存在就是为了解决这个重复计算的问题,在最开始求出目标路径后,把搜索过程的所有信息保存下来,等后面碰到了先验未知的障碍物时就可以利用一开始保存下来的信息快速的规划出新的路径。
顺便一提因为D*算法有上述的特性,所以D*算法可以使用在“无先验地图信息/先验地图信息不多的环境中的导航”的问题,因为只需要在最开始假装整个地图没有任何障碍,起点到终点的路径就是一条直线,然后再在在线运行时不断使用D*算法重新规划即可。
D*算法流程
# 伪代码
class state:
# 存储了每个地图格子所需的信息,下面会说到这个类用在哪。以下为类成员变量
x # 横坐标
y # 纵坐标
t = "new" # 记录了当前点是否被搜索过(可为“new”,"open", "close",分别代表这个格子没被搜索过,这个格子在open表里,这个格子在close表里。关于什么是open表什么是close表,建议去看A*算法,能很快理解)
parent = None # 父指针,沿着某个点的父指针一路搜索就能找到从这个点到目标点end的最短路径
h # 当前代价值(D*算法核心)
k # 历史最小代价值(D*算法核心,意义是所有更新过的h之中最小的h值)
function Dstar(map, start, end):
# map:m*n的地图,记录了障碍物。map[i][j]是一个state类对象
# start:起点,state类对象
# end: 终点,state类对象
open_list = [ ] # 新建一个open list用于引导搜索
insert_to_openlist(end,0, open_list) # 将终点放入open_list中
# 第一次搜索,基于离线先验地图找到从起点到终点的最短路径,注意从终点往起点找
loop until (start.t == “close”):process_state() # D*算法核心函数之一
end loop
# 让机器人一步一步沿着路径走,有可能在走的过程中会发现新障碍物
temp_p = start
while (p != end) do
if ( unknown obstacle found) then # 发现新障碍物
for new_obstacle in new_obstacles: # 对每个新障碍物调用modify_cost函数
modify_cost( new_obstacle ) #(D*算法核心函数之一)
end for
do
k_min = process_state()
while not ( k_min >= temp_p.h or open_list.isempty() )continue
end if
temp_p = temp_p.parent
end while
上述伪代码中核心函数为2个:modify_cost 和 process_state。我翻阅了csdn几个关于process_state的解释,发现都有挺大的错误,会让整个算法在某些情况下陷入死循环(比如D*规划算法及python实现_mhrobot的博客-CSDN博客)。而且就连原论文的伪代码都有点问题(可能原论文(Optimal and Effificient Path Planning for Partially-Known Environments,
function modify_cost( new_obstacle ):
set_cost(any point to new_obstacle ) = 10000000000 # 让“从任何点到障碍点的代价”和“从障碍点到任何点的代价” 均设置为一个超大的数(考虑8邻接)
if new_obstacle.state == "close" then
insert(new_obstacle, new_obstacle.h ) # 放到open表中,insert也是d*算法中的重要函数之一
end if
return get_min_k_(openlist) # 返回openlist中最小的k值
下面是 Process_state函数的伪代码,注意标红那条
function process_state( ):
x = get_min_k_state(oepn_list) # 拿出openlist中获取k值最小那个state,这点目的跟A*是一样的,都是利用k值引导搜索顺序,但注意这个k值相当于A*算法中的f值(f=g+h, g为实际代价函数值,h为估计代价启发函数值),而且在D*中,不使用h这个启发函数值, 仅使用实际代价值引导搜索,所以其实硬要说,D*更像dijkstra,都是使用实际代价引导搜索而不用启发函数缩减搜索范围,D*这点对于后面发现新障碍物进行重新规划来说是必要的。
if x == Null then return -1
k_old = get_min_k(oepn_list) # 找到openlist中最小的k值,其实就是上面那个x的k值
open_list,delete(x) # 将x从open list中移除, 放入close表
x.state = "close" # 相当于放入close表,只不过这里不显式地维护一个close表
# 以下为核心代码:
if k_old < x.h then # 满足这个条件说明x的h值被修改过,认为x处于raise状态
for each_neighbor Y of X: #考虑8邻接neighbor
if y.h<k_old and x.h> y.h + cost(y,x) then
x.parent = y
x.h = y.h + cost(x,y)
end if
end for
end if
# 第二组判断
if k_old == x.h then
for each_neighbor Y of X: #考虑8邻接neighbor
if y.state == "new" or
(y.parent == x and y.h !=x.h + cost(x,y) ) or
(y.parent != x and y.h >x.h + cost(x,y)) then
y.parent = x
insert(y, x.h + cost(x,y))
end if
end for
else: # 不满足k_old == x.h 那就是k_old < x.h
for each_neighbor Y of X: #考虑8邻接neighbor
if y.state == "new" or
(y.parent == x and y.h !=x.h + cost(x,y) ) then
y.parent = x
insert(y, x.h + cost(x,y))
else:
if (y.parent != x and y.h >x.h + cost(x,y)) then
x.k = x.h # 注意这行!没有这行会出现特定情况死循环。在查阅大量资料后,在wikipedia的d*算法页面中找到解决办法就是这行代码。网上大部分资料,包括d*原始论文里都是没这句的,不知道为啥
insert(x, x.h)
else:
if (y.parent!=x and x.h>y.h+cost(y,x) and y.parent = "close" and y.h>k_old then
insert(y,y.h)
end if
end if
end if
end for
end if
return get_min_k(oepn_list)