日撸java三百行day58

news2025/1/12 13:28:38

文章目录

说明
Day58 符号型数据的 NB 算法
- 1.基础理论知识
- - 1.1 条件概率
  - 1.2 独立性假设
  - 1.3 Laplacian 平滑
- 2. 符号型数据的预测算法跟踪
- - 2.1 testNominal()方法
  - - 2.1.1 NaiveBayes 构造函数
    - 2.1.2 calculateClassDistribution()
    - 2.1.3 calculateConditionalProbabilities()方法
    - 2.1.4 classify()方法
    - 2.1.5 computeAccuracy() 计算精确性

说明

闵老师的文章链接：日撸 Java 三百行（总述）_minfanphd的博客-CSDN博客
自己也把手敲的代码放在了github上维护：https://github.com/fulisha-ok/sampledata

Day58 符号型数据的 NB 算法

1.基础理论知识

（对老师这篇文章的翻译，以方便自己的理解）

1.1 条件概率

在给定某个条件下，事件发生的概率。它表示为 P(A|B)，表示在事件 B 发生的条件下事件 A 发生的概率。
P(AB) 表示事件 A和B同时发生的概率;
$\frac{p(AB)}{p(B)} = \frac{p(B|A)*p(A)}{p(B)}$

1.2 独立性假设

假设特征之间是相互独立的，在计算概率时，我们可以假设每个特征的出现与其他特征无关，这样可以简化计算过程（虽然这个假设在现实中并不总是成立）

在x发生的条件下Di发生的概率，且假设各个特征之间是相互独立的（直接可以展开连乘）。
x 条件组合，如outlook=sunny∧temperature=hot； Di 表示一个事件, 如: play = No不出去玩
$p(D_{i}|x)= \frac{p(xD_{i})}{p(x)}=\frac{p(D_{i})p(x|D_{i})}{p(x)}=\frac{p(D_{i})\prod_{j=1}^{m}p(x_{j}|D_{i})}{p(x)}$
计算P(x)还是很有困难的，想想如果特征值多了，那这个P(x)计算难度难以想象呀。我们的真正的目标是预测 $p(D_{i}|x)$ 属于那个类别最大，其实他们的分母都是一样的，我们当然就可以忽略了，去关注他的分子 $p(D_{i})\prod_{j=1}^{m}p(x_{j}|D_{i})$ 。
我们对未知样本进行分类时，对 $p(D_{i}|x)$ 的计算我们就忽略调分母，只考虑分子，并对等式两边取对数，这样乘法就变为加法，则预测方案就如下：

1.3 Laplacian 平滑

假设我们中有 $p(x_{j}|D_{i})=0$ 我们 $p(D_{i}|x) = 0$ , 进入文章中所说如果出现 $p(x_{j}|D_{i})=0$ 就有一票否决权了。所以引入Laplacian 平滑用于处理零概率问题。我通过一个简单的例子结合文章来理解：
假设下面是我们训练集数据：

outlook	temperature	paly
Sunny	Hot	No
Overcast	Mild	Yes
Rainy	Mild	Yes
Rainy	Cool	Yes
Overcast	hot	Yes

Di表示一个事件, 如: play = No
x就表示一个条件的组合。如outlook=sunny∧temperature=hot； xj就是某个特征取值。如outlook=sunny
我们根据上面训练数据集得：P(Play = Yes) = 4/5； P(Play = No) = 1/5
P(xj | Di) 如上：P(outlook = sunny | play = yes) = 0；P(temperature=hot∣play=yes) = 0，正因为有0的出现，我不管什么天气和温度，我打球的概率都变为0了，这样显然是不合理。加入Laplacian 平滑，在计算条件概率时，可以让训练数据中没有观察到某个特征时，它不是0概率。
Laplacian 平滑
结合文章中我们知道：在分子上，都加了1，分母加上特征取值类别个数，分子分母的概率都乘了n(测试样本数量)

例如：对条件概率P(xj | Di)进行平滑
$\frac{n*p(outlook = sunny∧play = yes) + 1}{n*p(play = yes) + 3}$

$\frac{5*0 + 1}{5*\frac{4}{5} + 3} = \frac{1}{7}$
$\frac{5*\frac{2}{5} + 1}{5*\frac{4}{5} + 3} = \frac{3}{7}$
$\frac{5*\frac{2}{5} + 1}{5*\frac{4}{5} + 3}= \frac{3}{7}$

2. 符号型数据的预测算法跟踪

我带着上面的思路去理解代码（从main方法开始看起）我主要通过debug来看各个变量数据的变化结果，用截图的方式展示。（变量太多了…,用debug理解更快）

2.1 testNominal()方法

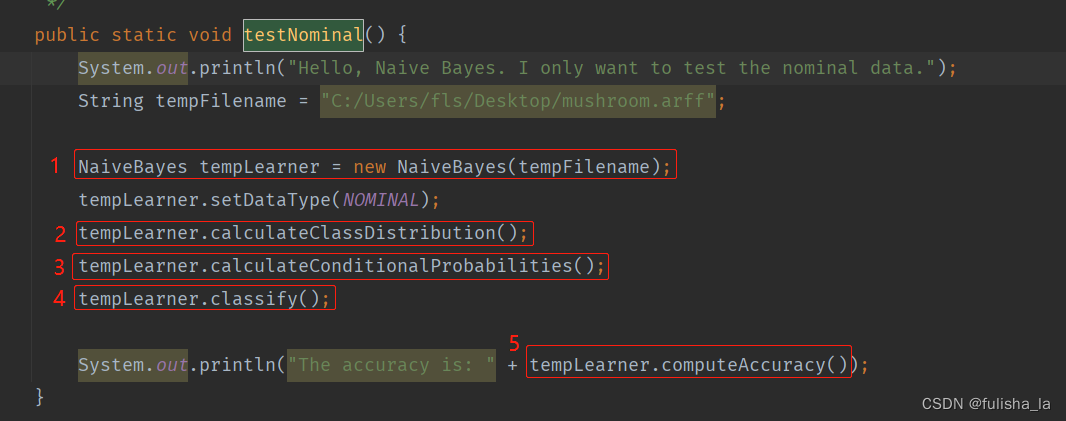
在这里插入图片描述

2.1.1 NaiveBayes 构造函数

构造函数主要是读文本内容，初始化数据。可知mushroom.arff文件有8124条数据集，22个特征，2中类别选择。
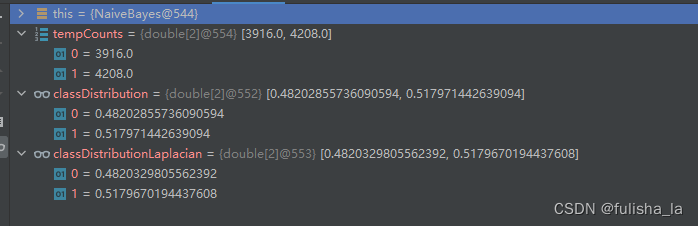
在这里插入图片描述

2.1.2 calculateClassDistribution()

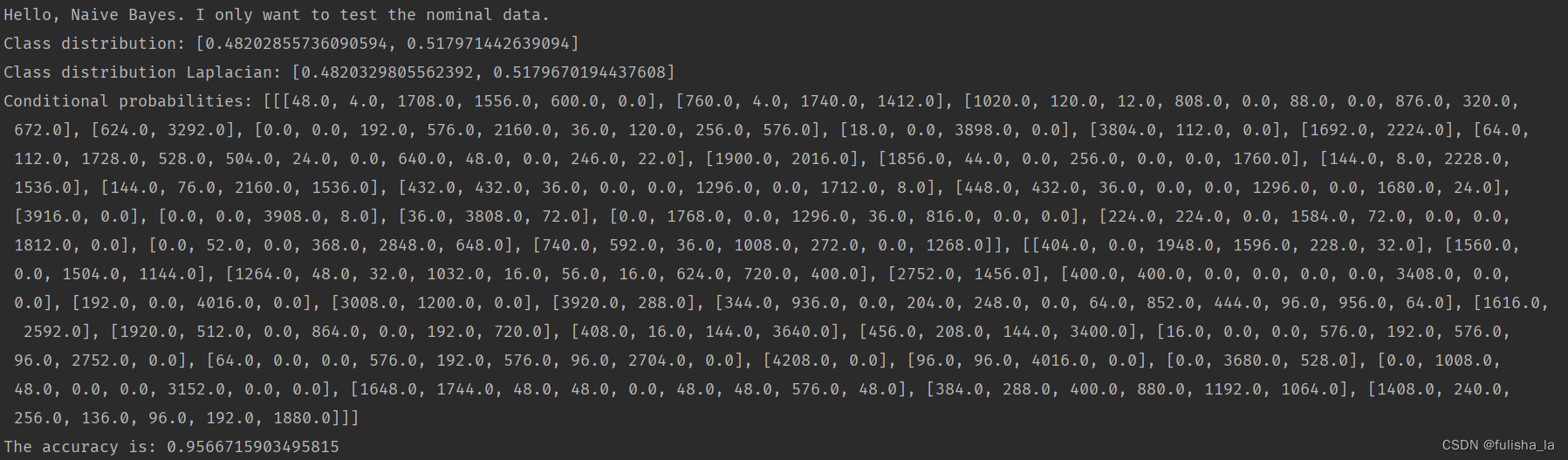
计算类别分布概率。

classDistribution 根据数据集计算不同类别的概率（就像上面我出去玩的概率是0.482028，不出去玩的概率是0.51797类似）
classDistributionLaplacian 是对classDistribution 进行拉普拉斯平滑后的类别分布

2.1.3 calculateConditionalProbabilities()方法

进行空间分配（conditionalCounts和conditionalProbabilitiesLaplacian变量在初始分配都一样）
一共有22个特征，其实对比文件和代码的赋值就一目了然了
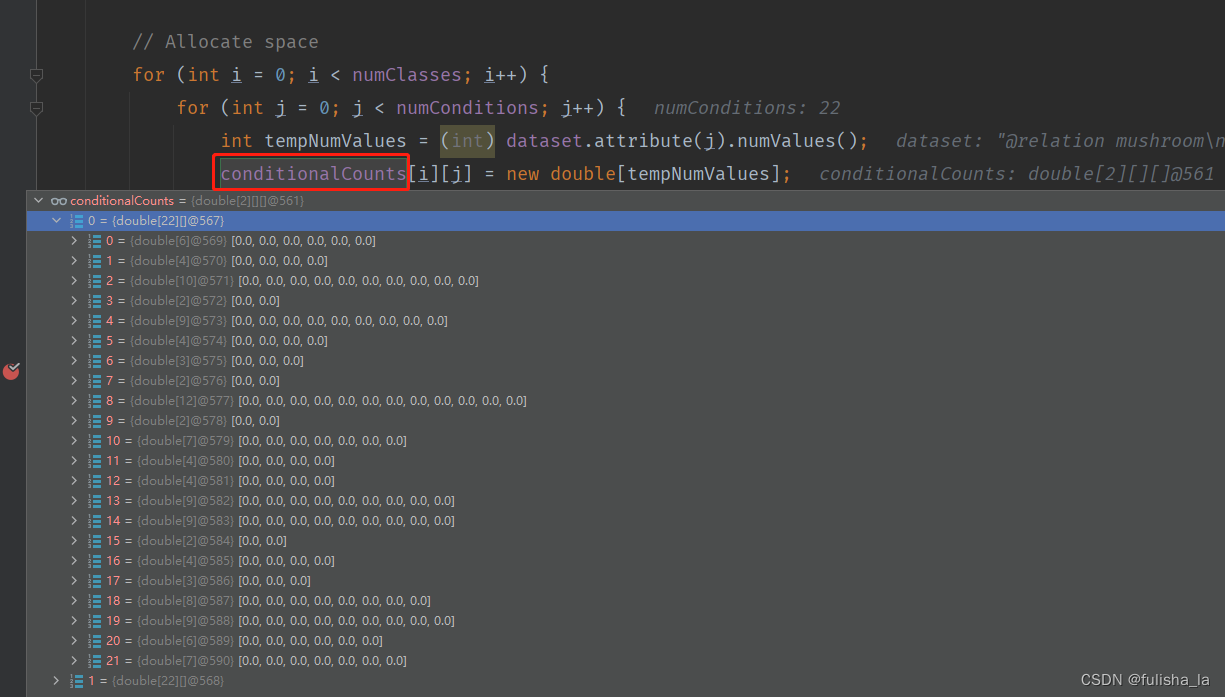
conditionalCounts赋值
我也是看了好一会儿才明白这个取值。就如我们以conditionalCounts[0][0][tempValue]来理解，这个的含义就是我们第一行的数据中的第一个特征值即值为x,x所在的索引为2，conditionalCounts[0][0][2] 就累加一个1。同理conditionalCounts[0][1][tempValue]就是看他第2个特征值所在的索引位置是多少，以此类推

结合原数据来看
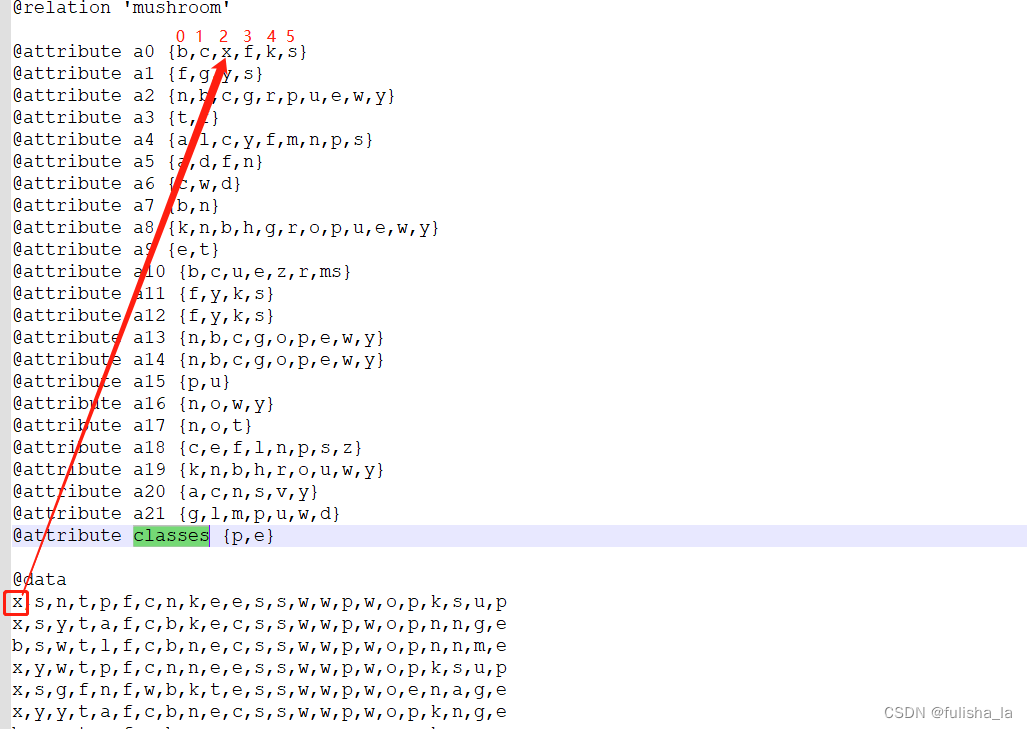
统计8124个数据样本出现在每个特征的次数（目的是为了方便计算后面的条件概率）
计算条件概率（conditionalProbabilitiesLaplacian赋值）（用Laplacian平滑）
结合上面Laplacian平滑基础知识即可，计算每个特征值出现的条件概率

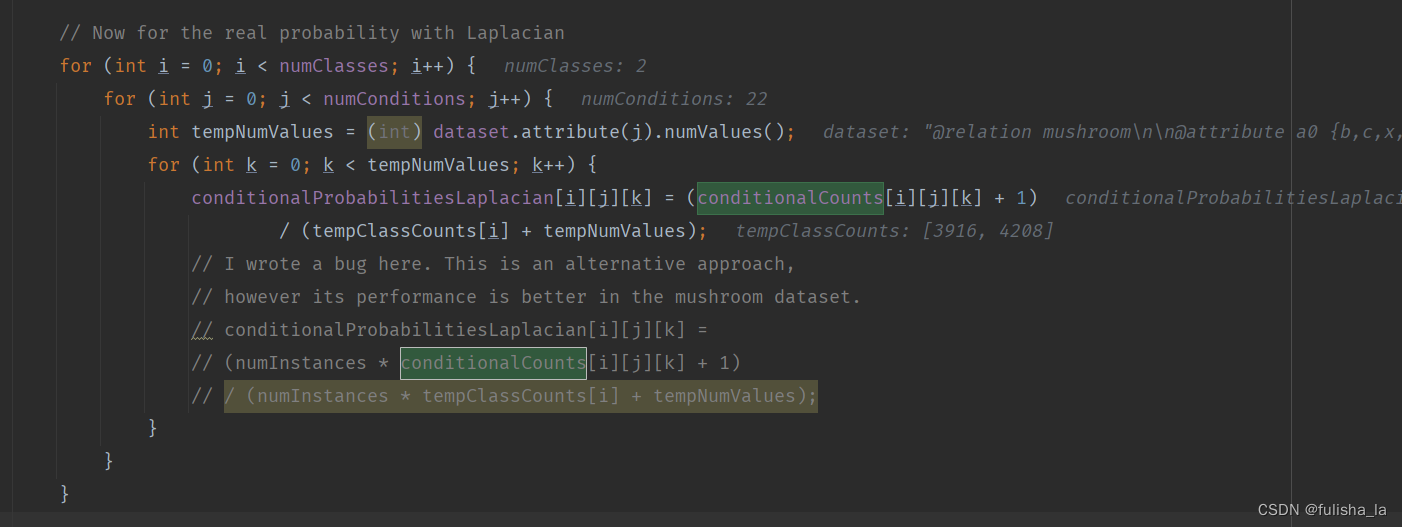
2.1.4 classify()方法

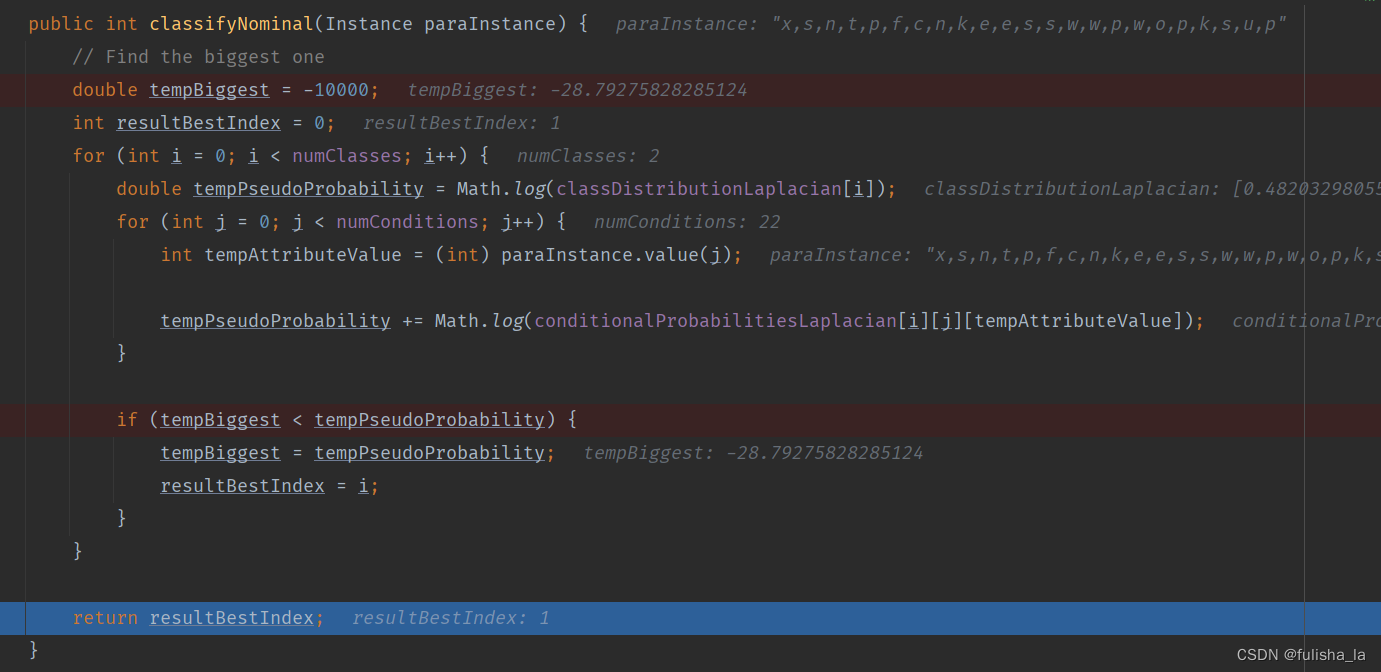
预测类别。在之前的代码中，已经把所有数据都准备好了，现在是结合这个公式去预测类别
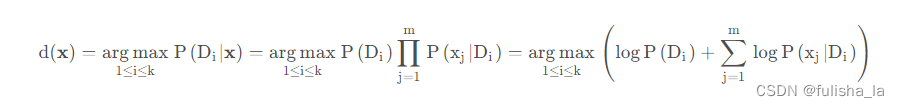
在这里插入图片描述

就如我们预测文本中这个数据行：x,s,n,t,p,f,c,n,k,e,e,s,s,w,w,p,w,o,p,k,s,u,p，我们根据上面这个公式预测出的结果是他类别为e即1（实际上他类别为p即0）
在这里插入图片描述

2.1.5 computeAccuracy() 计算精确性

    /**
     * Compute accuracy.
     * @return
     */
    public double computeAccuracy() {
        double tempCorrect = 0;
        for (int i = 0; i < numInstances; i++) {
            if (predicts[i] == (int) dataset.instance(i).classValue()) {
                tempCorrect++;
            }
        }

        double resultAccuracy = tempCorrect / numInstances;
        return resultAccuracy;
    }

代码结果：全部代码可以看文章链接。
在这里插入图片描述