[GWCTF 2019]babyRSA
解答过程在脚本内
from Crypto.Util.number import *
import gmpy2
import sympy
import z3
e = 0x10001
N=636585149594574746909030160182690866222909256464847291783000651837227921337237899651287943597773270944384034858925295744880727101606841413640006527614873110651410155893776548737823152943797884729130149758279127430044739254000426610922834573094957082589539445610828279428814524313491262061930512829074466232633130599104490893572093943832740301809630847541592548921200288222432789208650949937638303429456468889100192613859073752923812454212239908948930178355331390933536771065791817643978763045030833712326162883810638120029378337092938662174119747687899484603628344079493556601422498405360731958162719296160584042671057160241284852522913676264596201906163
m1=90009974341452243216986938028371257528604943208941176518717463554774967878152694586469377765296113165659498726012712288670458884373971419842750929287658640266219686646956929872115782173093979742958745121671928568709468526098715927189829600497283118051641107305128852697032053368115181216069626606165503465125725204875578701237789292966211824002761481815276666236869005129138862782476859103086726091860497614883282949955023222414333243193268564781621699870412557822404381213804026685831221430728290755597819259339616650158674713248841654338515199405532003173732520457813901170264713085107077001478083341339002069870585378257051150217511755761491021553239
m2=487443985757405173426628188375657117604235507936967522993257972108872283698305238454465723214226871414276788912058186197039821242912736742824080627680971802511206914394672159240206910735850651999316100014691067295708138639363203596244693995562780286637116394738250774129759021080197323724805414668042318806010652814405078769738548913675466181551005527065309515364950610137206393257148357659666687091662749848560225453826362271704292692847596339533229088038820532086109421158575841077601268713175097874083536249006018948789413238783922845633494023608865256071962856581229890043896939025613600564283391329331452199062858930374565991634191495137939574539546
# p q接近 可分解N得到pq
p=797862863902421984951231350430312260517773269684958456342860983236184129602390919026048496119757187702076499551310794177917920137646835888862706126924088411570997141257159563952725882214181185531209186972351469946269508511312863779123205322378452194261217016552527754513215520329499967108196968833163329724620251096080377747699
q=797862863902421984951231350430312260517773269684958456342860983236184129602390919026048496119757187702076499551310794177917920137646835888862706126924088411570997141257159563952725882214181185531209186972351469946269508511312863779123205322378452194261217016552527754513215520329499967108196968833163329724620251096080377748737
# 且可以通过prevprime得到 secret_num
# print(sympy.prevprime(p))
secret_num = 797862863902421984951231350430312260517773269684958456342860983236184129602390919026048496119757187702076499551310794177917920137646835888862706126924088411570997141257159563952725882214181185531209186972351469946269508511312863779123205322378452194261217016552527754513215520329499967108196968833163329724620251096080377746907
# 有了pq可以先拿到c1 和 c2
d = gmpy2.invert(e,(p-1)*(q-1))
c1 = int(pow(m1,d,N))
c2 = int(pow(m2,d,N))
# 然后我们知道c1 c2的两个等价关系
# 用z3来解
F1,F2 = z3.Ints("F1 F2")
s = z3.Solver()
s.add(F1+F2 == c1)
s.add(F1**3 + F2**3 == c2)
s.check()
print(s.model())
# [F2 = 1141553212031156130619789508463772513350070909,
# F1 = 1590956290598033029862556611630426044507841845]
F2 = 1141553212031156130619789508463772513350070909
F1 = 1590956290598033029862556611630426044507841845
print(long_to_bytes(F1)+long_to_bytes(F2))
[CISCN 2021初赛]rsa
小e
共模
p高位泄露
解得
O wild West Wind, thou breath of Autumn's being,
Thou, from whose unseen presence the leaves dead
Are driven, like ghosts from an enchanter fleeing,
Yellow, and black, and pale, and hectic red,
Pestilence-stricken multitudes: O thou,
Who chariotest to their dark wintry bed
然后发现这么搞有问题,我是没对上格式md5能对
所以用如下脚本
from Crypto.Util.number import *
import hashlib
m1 = 267334379257781603687613466720913534310764480084016847281446486946801530200295563483353634338157
m2 = 4193305853284549103821195807609492624095031428085219879448342104337322945001387680236011960472296815293233144303730273979905837762067652913308898433728800864776794638198055607422503065410595894676740531680367227696622352026247676452540064020322619036125381146346603655445487695574824919137
m3 = 978430871477569051989776547659020359721056838635797362474311886436116962354292851181720060000979143571198378856012391742078510586927376783797757539078239088349758644144812898155106623543650953940606543822567423130350207207895380499638001151443841997176299548692737056724423631882
print(hashlib.md5(long_to_bytes(m1)+long_to_bytes(m2)+long_to_bytes(m3)).hexdigest())
[LitCTF 2023]你是我的关键词(Keyworld) (初级)
关键词加解密
key是YOU
[RoarCTF 2019]babyRSA
这题考威尔逊定理
from Crypto.Util.number import *
import gmpy2
import sympy
def get_prime(A,B):
tem = 1
for i in range(B+1,A):
tem = (tem * i) % A
k = (-1*gmpy2.invert(tem,A))%A
return sympy.nextprime(k)
n = 85492663786275292159831603391083876175149354309327673008716627650718160585639723100793347534649628330416631255660901307533909900431413447524262332232659153047067908693481947121069070451562822417357656432171870951184673132554213690123308042697361969986360375060954702920656364144154145812838558365334172935931441424096270206140691814662318562696925767991937369782627908408239087358033165410020690152067715711112732252038588432896758405898709010342467882264362733
e = 0x1001
c = 75700883021669577739329316795450706204502635802310731477156998834710820770245219468703245302009998932067080383977560299708060476222089630209972629755965140317526034680452483360917378812244365884527186056341888615564335560765053550155758362271622330017433403027261127561225585912484777829588501213961110690451987625502701331485141639684356427316905122995759825241133872734362716041819819948645662803292418802204430874521342108413623635150475963121220095236776428
A1=21856963452461630437348278434191434000066076750419027493852463513469865262064340836613831066602300959772632397773487317560339056658299954464169264467234407
B1=21856963452461630437348278434191434000066076750419027493852463513469865262064340836613831066602300959772632397773487317560339056658299954464169264467140596
A2=16466113115839228119767887899308820025749260933863446888224167169857612178664139545726340867406790754560227516013796269941438076818194617030304851858418927
B2=16466113115839228119767887899308820025749260933863446888224167169857612178664139545726340867406790754560227516013796269941438076818194617030304851858351026
p = get_prime(A1,B1)
q = get_prime(A2,B2)
r = n // p // q
d = gmpy2.invert(e,(p-1)*(q-1)*(r-1))
print(long_to_bytes(pow(c,d,n)))
[LitCTF 2023]Is this only base?
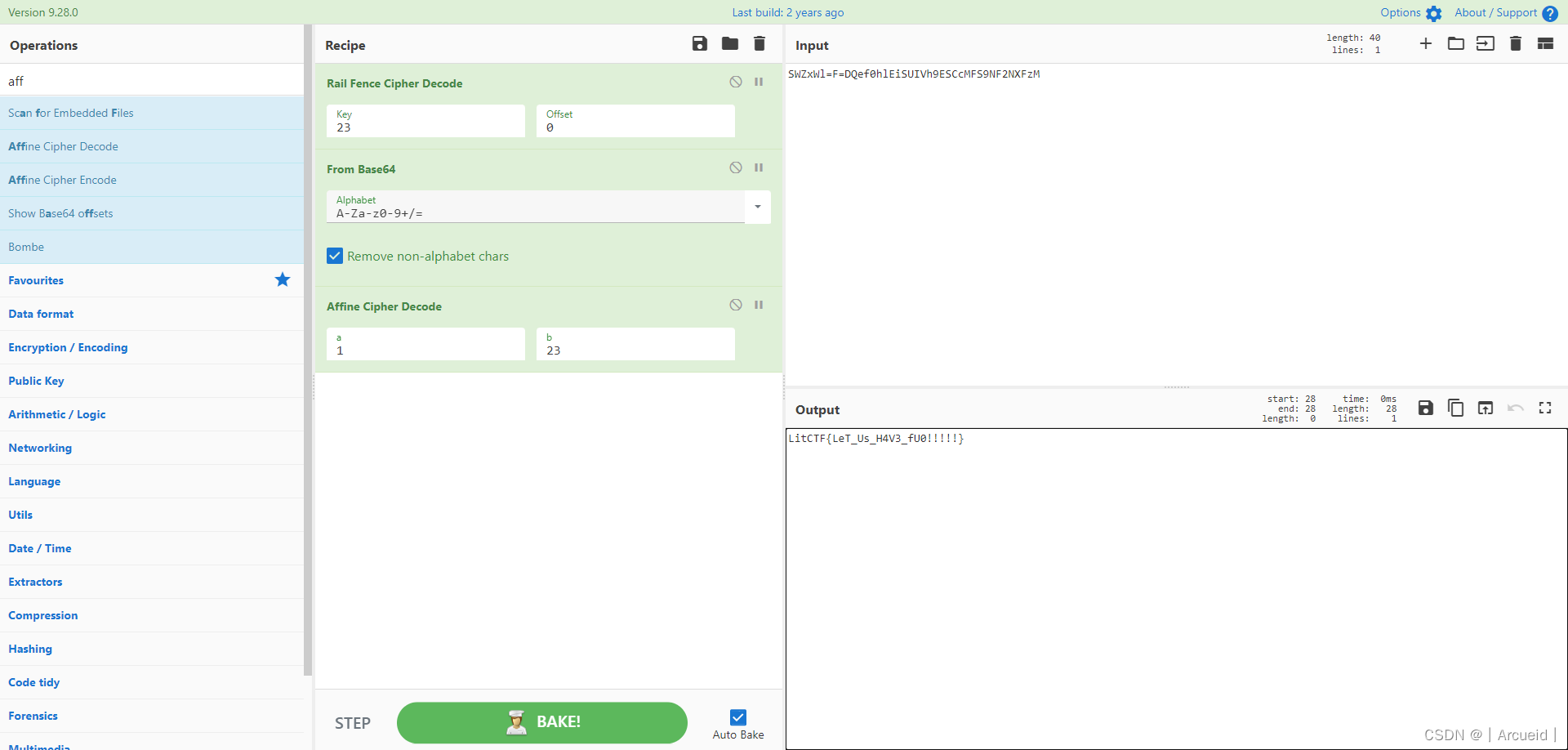
[RoarCTF 2019]RSA
n能分解
from Crypto.Util.number import *
import gmpy2
A = 2683349182678714524247469512793476009861014781004924905484127480308161377768192868061561886577048646432382128960881487463427414176114486885830693959404989743229103516924432512724195654425703453612710310587164417035878308390676612592848750287387318129424195208623440294647817367740878211949147526287091298307480502897462279102572556822231669438279317474828479089719046386411971105448723910594710418093977044179949800373224354729179833393219827789389078869290217569511230868967647963089430594258815146362187250855166897553056073744582946148472068334167445499314471518357535261186318756327890016183228412253724
n = 117930806043507374325982291823027285148807239117987369609583515353889814856088099671454394340816761242974462268435911765045576377767711593100416932019831889059333166946263184861287975722954992219766493089630810876984781113645362450398009234556085330943125568377741065242183073882558834603430862598066786475299918395341014877416901185392905676043795425126968745185649565106322336954427505104906770493155723995382318346714944184577894150229037758434597242564815299174950147754426950251419204917376517360505024549691723683358170823416757973059354784142601436519500811159036795034676360028928301979780528294114933347127
c = 41971850275428383625653350824107291609587853887037624239544762751558838294718672159979929266922528917912189124713273673948051464226519605803745171340724343705832198554680196798623263806617998072496026019940476324971696928551159371970207365741517064295956376809297272541800647747885170905737868568000101029143923792003486793278197051326716680212726111099439262589341050943913401067673851885114314709706016622157285023272496793595281054074260451116213815934843317894898883215362289599366101018081513215120728297131352439066930452281829446586562062242527329672575620261776042653626411730955819001674118193293313612128
# A=(((y%x)**5)%(x%y))**2019+y**316+(y+1)/x
# p=next_prime(z*x*y)
# q=next_prime(z)
p=139916095583110895133596833227506693679306709873174024876891023355860781981175916446323044732913066880786918629089023499311703408489151181886568535621008644997971982182426706592551291084007983387911006261442519635405457077292515085160744169867410973960652081452455371451222265819051559818441257438021073941183
q=842868045681390934539739959201847552284980179958879667933078453950968566151662147267006293571765463137270594151138695778986165111380428806545593588078365331313084230014618714412959584843421586674162688321942889369912392031882620994944241987153078156389470370195514285850736541078623854327959382156753458569
for e in range(1,1000000):
try:
d = gmpy2.invert(e,(p-1)*(q-1))
flag = long_to_bytes(pow(c,d,n))
if b'CTF{' in flag:
print(flag)
break
except:
continue
另一种做法是解x和y
from Crypto.Util.number import *
import gmpy2
import sympy
A = 2683349182678714524247469512793476009861014781004924905484127480308161377768192868061561886577048646432382128960881487463427414176114486885830693959404989743229103516924432512724195654425703453612710310587164417035878308390676612592848750287387318129424195208623440294647817367740878211949147526287091298307480502897462279102572556822231669438279317474828479089719046386411971105448723910594710418093977044179949800373224354729179833393219827789389078869290217569511230868967647963089430594258815146362187250855166897553056073744582946148472068334167445499314471518357535261186318756327890016183228412253724
n = 117930806043507374325982291823027285148807239117987369609583515353889814856088099671454394340816761242974462268435911765045576377767711593100416932019831889059333166946263184861287975722954992219766493089630810876984781113645362450398009234556085330943125568377741065242183073882558834603430862598066786475299918395341014877416901185392905676043795425126968745185649565106322336954427505104906770493155723995382318346714944184577894150229037758434597242564815299174950147754426950251419204917376517360505024549691723683358170823416757973059354784142601436519500811159036795034676360028928301979780528294114933347127
c = 41971850275428383625653350824107291609587853887037624239544762751558838294718672159979929266922528917912189124713273673948051464226519605803745171340724343705832198554680196798623263806617998072496026019940476324971696928551159371970207365741517064295956376809297272541800647747885170905737868568000101029143923792003486793278197051326716680212726111099439262589341050943913401067673851885114314709706016622157285023272496793595281054074260451116213815934843317894898883215362289599366101018081513215120728297131352439066930452281829446586562062242527329672575620261776042653626411730955819001674118193293313612128
# A=(((y%x)**5)%(x%y))**2019+y**316+(y+1)/x
# p=next_prime(z*x*y)
# q=next_prime(z)
def get_x_y():
for x in range(2,1000):
for y in range(2,1000):
try:
res = (((y%x)**5)%(x%y))**2019+y**316+(y+1)//x
if A == res:
return x,y
except:
pass
def get_p(x,y):
tem = n // (x*y)
p = gmpy2.iroot(tem,2)[0]
while True:
p = sympy.nextprime(p)
if n % p == 0 :
return p
x, y = get_x_y()
p = get_p(x,y)
q = n // p
for e in range(1,1000000):
try:
d = gmpy2.invert(e,(p-1)*(q-1))
flag = long_to_bytes(pow(c,d,n))
if b'CTF{' in flag:
print(flag)
break
except:
continue
[AFCTF 2018]Single
https://quipqiup.com/一把梭
[NSSCTF 2022 Spring Recruit]factor
import hashlib
p=13891650093628440437
q=17315890900809982861
print(hashlib.md5(str(p+q).encode()).hexdigest())
[鹤城杯 2021]BabyRSA
已知p高位q低位
由
N
≡
p
l
∗
q
l
m
o
d
2
265
P
l
≡
N
∗
q
l
−
1
m
o
d
2
265
\begin{array}{l} N \equiv p_{l} * q_{l} \bmod 2^{265} \\ P_{l} \equiv N * q_{l}^{-1} \bmod 2^{265} \end{array}
N≡pl∗qlmod2265Pl≡N∗ql−1mod2265
可以得到
p
l
p_{l}
pl
coppersmith打p
脚本如下
#sage
from Crypto.Util.number import *
import gmpy2
c = 19073695285772829730103928222962723784199491145730661021332365516942301513989932980896145664842527253998170902799883262567366661277268801440634319694884564820420852947935710798269700777126717746701065483129644585829522353341718916661536894041337878440111845645200627940640539279744348235772441988748977191513786620459922039153862250137904894008551515928486867493608757307981955335488977402307933930592035163126858060189156114410872337004784951228340994743202032248681976932591575016798640429231399974090325134545852080425047146251781339862753527319093938929691759486362536986249207187765947926921267520150073408188188
ph = 1514296530850131082973956029074258536069144071110652176122006763622293335057110441067910479
ql = 40812438243894343296354573724131194431453023461572200856406939246297219541329623
n = 21815431662065695412834116602474344081782093119269423403335882867255834302242945742413692949886248581138784199165404321893594820375775454774521554409598568793217997859258282700084148322905405227238617443766062207618899209593375881728671746850745598576485323702483634599597393910908142659231071532803602701147251570567032402848145462183405098097523810358199597631612616833723150146418889589492395974359466777040500971885443881359700735149623177757865032984744576285054725506299888069904106805731600019058631951255795316571242969336763938805465676269140733371287244624066632153110685509892188900004952700111937292221969
e = 65537
pl = n * gmpy2.invert(ql,2**265) % 2**265
pbits = 1024
PR.<x> = PolynomialRing(Zmod(n))
ph = ph << 724
for i in range(2**6):
f = ph + 2^265 * x * 2**6 + pl + i*2^265
f = f.monic()
p = f.small_roots(X=2^(459-6),beta=0.4)
if p:
p = ph + 2^265 * int(p[0]) * 2**6 + pl + i*2^265
print(p)
break
q = n // p
d = gmpy2.invert(e,(p-1)*(q-1))
print(long_to_bytes(pow(c,d,n)))
这里直接打不行,就爆破几位
[LitCTF 2023]原来你也玩原神 (初级)
网上找个原的图一个个对
LITCTF{YUANLAINIYEWANYUANSHENWWW}
[LitCTF 2023]家人们!谁懂啊,RSA签到都不会 (初级)
[HDCTF 2023]Normal_Rsa
直接给了明文密码
[HGAME 2022 week2]RSA Attack2
共享素数
小e
共模
hgame{RsA@hAS!a&VArIETY?of.AttacK^mEThodS^whAT:other!AttACK|METHOdS~do@you_KNOW}
[NCTF 2019]childRSA
p-1光滑
python -m primefac -vs -m=p-1慢慢跑
一分钟左右能出
[HUBUCTF 2022 新生赛]RSAaaa
from Crypto.Util.number import *
import gmpy2
s = "473878130775 40132555282 40132555282 94619939727 72818765591 208015808884 42561234694 159353248388 27748063975 159353248388 159353248388 278953790403 410746718603 496849210942 27748063975 142521857906 103632267191 17774494147 328684046745 278953790403 129956887006 129956887006 366275425558 328684046745 142521857906 410746718603 142521857906 129956887006 379067009467 328684046745 159353248388 366275425558 129956887006 103632267191 27748063975 27748063975 17774494147 160623996897 278953790403 182341799525"
n = 536970330703
p=540961
q=992623
e = 65537
d = gmpy2.invert(e,(p-1)*(q-1))
for i in s.split(" "):
print(long_to_bytes(pow(int(i),d,n)).decode(),end='')
[CISCN 2022 西南]rsa
题给了一堆没用的条件
关键在lcm = gmpy2.lcm(P-1, Q-1)
lcm(P-1,Q-1) // gcd(P-1,Q-1) = (P-1)(Q-1)
而rsa生成的 (P-1)(Q-1)大概率互素
尝试用1先试试,就解出来了
from Crypto.Util.number import *
import gmpy2
E = 65537
c = 4288727484183191191687364666620023549392656794153112764357730676861570386983002380982803054964588111708662498647767438881892355599604826306427809017097724346976778230464708540600157055782723189971534549543664668430013171469625043063261219462210251726207552819381767396148632877168530609902046293626355744288863460554297860696918890189350721960355460410677203131993419723440382095665713164422367291153108363066159712951217816814873413423853338021627653555202253351957999686659021298525147460016557904084617528199284448056532965033560516083489693334373695545423561715471204868795248569806148395196572046378679014697206
N = 17168634922359080770731181740188997952741812682116912079000170434755630873073792773455352815549564103486063484001457037305375162580861025543369063596825489461609724794798857499401637867986508655873564997664216374116361942711233205374363245780323485119184650145879389879046988234947922412374890843297813248828996855478005656041814919367820336728271583686844991928889831691815821365423570311291064846736832327637944358854661523107817781673029406341843040857813841671405147146887291204140157388049394514390098066284975682117038362207142272098796924412602725857521665773622056312191400612944442008222587867782281556388669
phi = 4292158730589770192682795435047249488185453170529228019750042608688907718268448193363838203887391025871515871000364259326343790645215256385842265899206372365402431198699714374850409466996627163968391249416054093529090485677808301343590811445080871279796162536469847469761747058736980603093722710824453312207182881241846080117790728778291633761198069016865260030288832065807438020772711645648333908622890343009942617559434851450007195025869850769670769715654662127278293639938359741401336592219730356884542179574372134014927006215640945952229142436595334916765255426954857520777553915330597952622785359222832224632624
d = gmpy2.invert(E,phi)
print(long_to_bytes(pow(c,d,N)))
[SWPUCTF 2021 新生赛]crypto3
数学推导过程参考
https://blog.csdn.net/qq_51999772/article/details/120926547
#sage
from Crypto.Util.number import *
c1= 17893542812755845772427795161304049467610774531005620109503081344099161906017295486868699578946474114607624347167976713200068059018517606363517478396368430072890681401898145302336139240273132723451063402106360810413024642916851746118524166947301681245568333254648265529408446609050354235727237078987509705857
c2= 95580409405085606847879727622943874726633827220524165744517624606566789614499137069562997931972825651309707390763700301965277040876322904891716953565845966918293178547100704981251056401939781365264616997055296773593435626490578886752446381493929807909671245959154990639046333135728431707979143972145708806954
n= 140457323583824160338989317689698102738341061967768153879646505422358544720607476140977064053629005764551339082120337223672330979298373653766782620973454095507484118565884885623328751648660379894592063436924903894986994746394508539721459355200184089470977772075720319482839923856979166319700474349042326898971
PR.<m> = PolynomialRing(Zmod(n))
f = m**2 - m*(c1+c2) + c1*c2
m = f.small_roots()
print(long_to_bytes(int(m[0])))
[HGAME 2022 week3]Multi Prime RSA
from Crypto.Util.number import *
import gmpy2
# n = p ** 2 * q ** 3 * r ** 5 * s ** 7
p = 61789932148719477384027458333380568978056286136137829092952317307711908353477
q = 91207969353355763685633284378833506319794714507027332929290701748727534193861
r = 105471299607375388622347272479207944509670502835651250945203397530010861809367
s = 83153238748903772448138307505579799277162652151244477391465130504267171881437
n = 1039344372165087100001063920598151812324151064684841845250974758525265148567706103784958424873181721352440209284812493753972556519482026327282644619091466886523804841248277210353173383407944598453848113815866908595335619458549486958764490103808475329598085842184963065068499489886467911087295087163762599284622055185456905774507245781667293199205317692029829495961487347944813874415423771980660778986211145841712412631156369129146470119135136378158203459576596246169191419488560832734046076107673091995860021863239882608638458149930255944184863801278386551031980146460231515747754411678651752698881001464973981424240781413084941947261875289725538959720572496329348499870580057997540844488309111059240745081048324762866572948371222839278718034435739827677190025500802453626872356208612718417249649474571197167076916403582394186357812640566250930361276229969553128128312736245440129556020108188835966131425956431796417720436474093381770796431629523054378258497546013222494974549262140415585158985940966415459478150722832119691308697510189026447359189994055885090735411738332296254011208547676914004864732327863884217733456287369771087094514708468685641820375220835485053482570852619363091173324203334503461823983610886849930944250553928855506012684504211525542998575275626784129736345142772399109273619522445919
e = 65537
c = 844677395496466411520394190869787261209960246734415406217975986418865760680024542119231873259131861208878522030009923057991526761346423130242121884493257732067700857897379859545356609151834223804262174935191718271211809221730601602827122249238086030580971376104724987801049500689134122609834321586609223761140538079460830213824674361601046367637227094018381901291488659642720549583856812747877519600804325570421770575999289389175021646347371879234023647657507178519047236746071420327155188213839293382288787853777540226192644761028822256165706787395891134765908229036044468473519166141610604791485071702808854944672418124203289328124793348198048601338476086482318248264508789781967910205393740835345086784345145351367491197717933757414967811594913692588314161669333147733048171044386546892346475181197482702164468542430187885074163177843285948999943328049159021873821254267471067523609151007885131921896462161216356454116929796355815756642621369974260365378070336290542971599886325232821981080341858950609157813769416455337935096696635623426418166316737131174435618543058086342714723330814586496030805366321181723292731710369013923285787724941830672247377301048663929453294620044701627159066468762709113137517559435822623284148112827473010030736329596829357275518641576798298066541516764673029908084962144713
phi = p*(p-1)*q**2*(q-1)*r**4*(r-1)*s**6*(s-1)
d = gmpy2.invert(e,phi)
print(long_to_bytes(pow(c,d,n)))
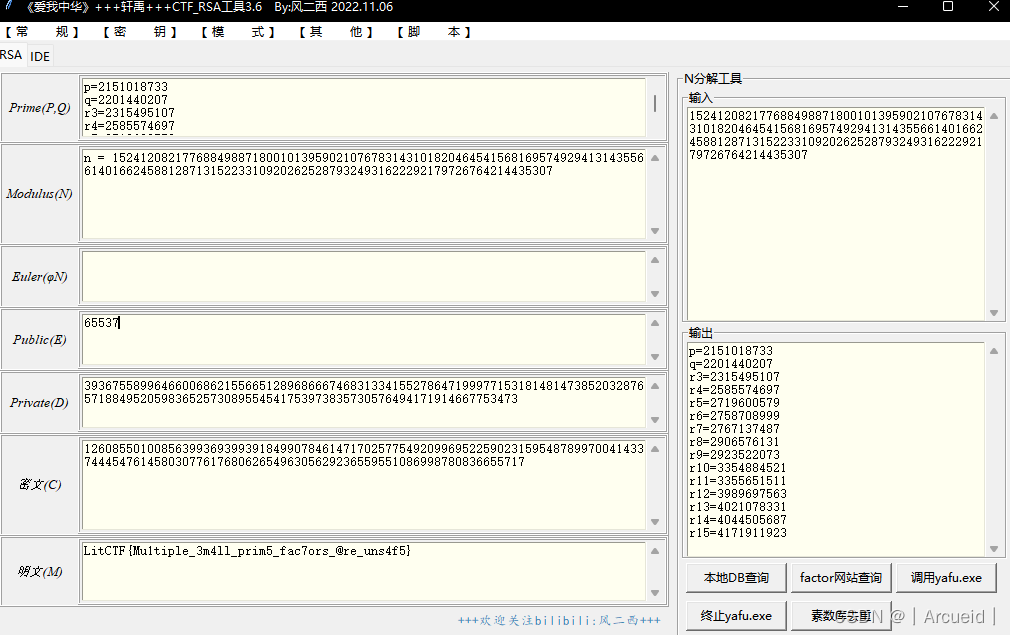
[LitCTF 2023]yafu (中级)
[AFCTF 2018]可怜的RSA
n可分解
为什么不能用pow解
可以看3tefanie丶zhou师傅的wp
https://blog.csdn.net/luochen2436/article/details/125872642