503.下一个更大元素II

教程视频：https://www.bilibili.com/video/BV15y4y1o7Dw
在这里插入图片描述

解法一：单调栈（两次遍历解决环状问题）

class Solution {
    public int[] nextGreaterElements(int[] nums) {
        int[] result = new int[nums.length];
        Arrays.fill(result, -1);
        Deque<Integer> stack = new LinkedList<>();
        stack.push(0);
        int n = nums.length;
        for(int i=1;i<2*n;i++){
            if(nums[i%n]<=nums[stack.peek()]){
                stack.push(i%n);
            }else{
                while(!stack.isEmpty() && nums[i%n]>nums[stack.peek()]){
                    result[stack.peek()]=nums[i%n];
                    stack.pop();
                }
                stack.push(i%n);
            }
        }
        return result;
    }
}

42. 接雨水

教程视频：https://www.bilibili.com/video/BV1uD4y1u75P
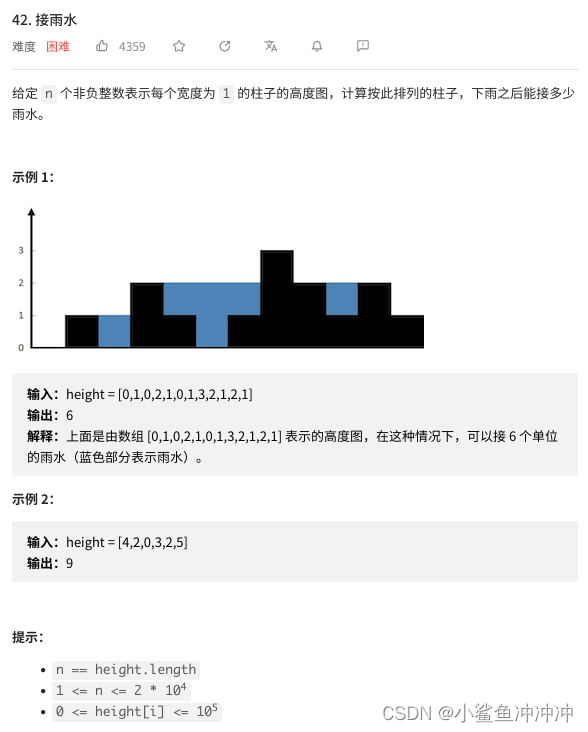
在这里插入图片描述

解法一：单调栈（横向累计）

找到左右第一个比当前元素高的值，选其中小的高督察乘以宽度得到当前雨水层的水。
在这里插入图片描述

class Solution {
    public int trap(int[] height) {
        Deque<Integer> stack = new LinkedList<>();
        stack.push(0);
        int result=0;
        for(int i=1;i<height.length;i++){
            if(height[i]<height[stack.peek()]){
                stack.push(i);
            }else if(height[i]==height[stack.peek()]){
                // 因为相等的相邻墙，左边一个是不可能存放雨水的，所以pop左边(前一个)index, push当前的index
                stack.pop();
                stack.push(i);
            }else{
                while(!stack.isEmpty() && height[i]>height[stack.peek()]){
                    int curIndex = stack.pop();
                    if(!stack.isEmpty()){//左侧遍历过的元素，大于当前值的最近元素就在栈口第二个位置
                        // System.out.println("right: "+i+", "+height[i]+", mid: "+curIndex+", "+height[curIndex]+", left: "+stack.peek()+", "+height[stack.peek()]);
                        int h = Math.min(height[i], height[stack.peek()])-height[curIndex];
                        int w = i-stack.peek()-1;
                        result+=h*w;
                    }
                }
                stack.push(i);
            }
        }
        return result;
    }
}

解法二：暴力解法

按照列来计算，比较容易理解。如果按照列来计算的话，宽度一定是1了，我们再把每一列的雨水的高度求出来就可以了。
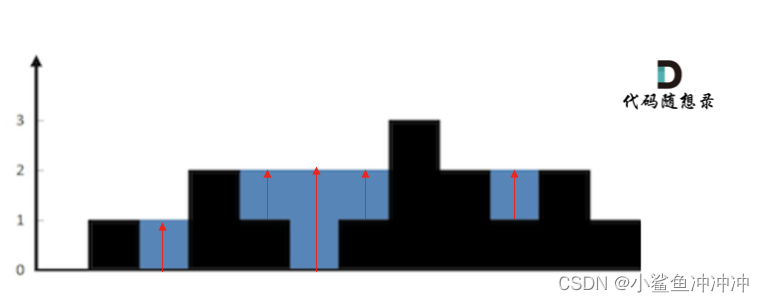
在这里插入图片描述
可以看出每一列雨水的高度，取决该列 左侧最高的柱子 和 右侧最高的柱子 中最矮的那个柱子的高度。

首先从头遍历所有的列，并且要注意第一个柱子和最后一个柱子不接雨水。在for循环中求左右两边最高柱子。最后，计算该列的雨水高度。

因为每次遍历列的时候，还要向两边寻找最高的列，所以时间复杂度为O(n^2)，空间复杂度为O(1)。
力扣上暴力解法超时了。

class Solution {
    public int trap(int[] height) {
        int result=0;
        for(int i=0;i<height.length;i++){
            if(i==0 || i==height.length-1){
                continue;
            }
            int leftMax = height[i];
            int rightMax = height[i];
            for(int j=i-1;j>=0;j--){
                if(height[j] > leftMax) leftMax = height[j];
            }
            for(int j=i+1;j<height.length;j++){
                if(height[j]>rightMax) rightMax =height[j];
            }
            if(leftMax!=0 && rightMax!=0){
                result+=Math.min(leftMax, rightMax)-height[i];
            }
        }
        return result;
    }
}

解法三：双指针优化

为了得到两边的最高高度，使用了双指针来遍历，每到一个柱子都向两边遍历一遍，这其实是有重复计算的。我们把每一个位置的左边最高高度记录在一个数组上（maxLeft），右边最高高度记录在一个数组上（maxRight），这样就避免了重复计算。

当前位置，左边的最高高度是前一个位置的左边最高高度和本高度的最大值。
从左向右遍历：maxLeft[i] = max(height[i], maxLeft[i - 1]);
从右向左遍历：maxRight[i] = max(height[i], maxRight[i + 1]);

class Solution {
    public int trap(int[] height) {
        int length = height.length;
        if (length <= 2) return 0;
        //记录左右诸子的最大高度，避免重复遍历
        int[] maxLeft = new int[length];
        int[] maxRight = new int[length];

        // 记录每个柱子左边柱子最大高度
        maxLeft[0] = height[0];
        for (int i = 1; i< length; i++) maxLeft[i] = Math.max(height[i], maxLeft[i-1]);

        // 记录每个柱子右边柱子最大高度
        maxRight[length - 1] = height[length - 1];
        for(int i = length - 2; i >= 0; i--) maxRight[i] = Math.max(height[i], maxRight[i+1]);

        // 求和
        int result = 0;
        for (int i = 0; i < length; i++) {
            int count = Math.min(maxLeft[i], maxRight[i]) - height[i];
            if (count > 0) result += count;
        }
        return result;
    }
}