目录

52. N皇后 II N Queens II  🌟🌟🌟

53. 最大子数组和  Maximum Subarray  🌟🌟

54. 螺旋矩阵 Spiral Matrix  🌟🌟

🌟 每日一练刷题专栏 🌟

Rust每日一练 专栏

Golang每日一练 专栏

Python每日一练 专栏

C/C++每日一练 专栏

Java每日一练 专栏

---

52. N皇后 II N Queens II

n 皇后问题 研究的是如何将 n 个皇后放置在 n × n 的棋盘上，并且使皇后彼此之间不能相互攻击。

给你一个整数 n ，返回 n 皇后问题 不同的解决方案的数量。

示例 1：

输入：n = 4
输出：2
解释：如上图所示，4 皇后问题存在两个不同的解法。

示例 2：

输入：n = 1
输出：1

提示：

• 1 <= n <= 9

相关题目： 

51. N 皇后 N-Queens  🌟🌟🌟 

代码1： 回溯法

fn total_n_queens(n: i32) -> i32 {
    let mut res = 0;
    let mut queens = vec![0; n as usize];
    fn backtrack(row: usize, queens: &mut [i32], res: &mut i32) {
        if row == queens.len() {
            *res += 1;
            return;
        }
        for col in 0..queens.len() {
            if is_not_under_attack(queens, row, col) {
                queens[row] = col as i32;
                backtrack(row + 1, queens, res);
                queens[row] = 0;
            }
        }
    }
    backtrack(0, &mut queens, &mut res);
    res
}

fn is_not_under_attack(queens: &[i32], row: usize, col: usize) -> bool {
    for i in 0..row {
        if queens[i] == col as i32 || queens[i] + i as i32 == row as i32 + col as i32
            || queens[i] - i as i32 == col as i32 - row as i32
        {
            return false;
        }
    }
    true
}

fn main() {
    println!("{}", total_n_queens(4));
    println!("{}", total_n_queens(1));
}

代码2： 位运算+dfs

fn total_n_queens(n: i32) -> i32 {
    let mut res = 0;
    fn dfs(row: i32, columns: &mut [bool], diagonals1: &mut [bool], diagonals2: &mut [bool], n: i32, res: &mut i32) {
        if row == n {
            *res += 1;
            return;
        }
        for col in 0..n {
            let index1 = (n - 1) + (col - row);
            let index2 = row + col;
            if !columns[col as usize] && !diagonals1[index1 as usize] && !diagonals2[index2 as usize] {
                columns[col as usize] = true;
                diagonals1[index1 as usize] = true;
                diagonals2[index2 as usize] = true;
                dfs(row + 1, columns, diagonals1, diagonals2, n, res);
                columns[col as usize] = false;
                diagonals1[index1 as usize] = false;
                diagonals2[index2 as usize] = false;
            }
        }
    }
    dfs(0, &mut vec![false; n as usize], &mut vec![false; 2 * n as usize - 1], &mut vec![false; 2 * n as usize - 1], n, &mut res);
    res
}

fn main() {
    println!("{}", total_n_queens(4));
    println!("{}", total_n_queens(1));
}

输出：

2
1 

---

53. 最大子数组和  Maximum Subarray

给你一个整数数组 nums ，请你找出一个具有最大和的连续子数组（子数组最少包含一个元素），返回其最大和。

子数组 是数组中的一个连续部分。

示例 1：

输入：nums = [-2,1,-3,4,-1,2,1,-5,4]
输出：6
解释：连续子数组 [4,-1,2,1] 的和最大，为 6 。

示例 2：

输入：nums = [1]
输出：1

示例 3：

输入：nums = [5,4,-1,7,8]
输出：23

提示：

• 1 <= nums.length <= 10^5
• -10^4 <= nums[i] <= 10^4

进阶：如果你已经实现复杂度为 O(n) 的解法，尝试使用更为精妙的 分治法 求解。

代码1： 动态规划

fn max_sub_array(nums: &[i32]) -> i32 {
    let n = nums.len();
    let mut dp = vec![0; n];
    dp[0] = nums[0];
    for i in 1..n {
        dp[i] = std::cmp::max(dp[i-1] + nums[i], nums[i]);
    }
    let mut res = dp[0];
    for i in 1..n {
        res = std::cmp::max(res, dp[i]);
    }
    res
}

fn main() {
    let nums = vec![-2, 1, -3, 4, -1, 2, 1, -5, 4];
    println!("{}", max_sub_array(&nums));
    let nums = vec![1];
    println!("{}", max_sub_array(&nums));
    let nums = vec![5,4,-1,7,8];
    println!("{}", max_sub_array(&nums));
}

代码2： 贪心算法

fn max_sub_array(nums: &[i32]) -> i32 {
    let n = nums.len();
    let (mut cur_sum, mut max_sum) = (0, nums[0]);
    for i in 0..n {
        cur_sum += nums[i];
        if cur_sum > max_sum {
            max_sum = cur_sum;
        }
        if cur_sum < 0 {
            cur_sum = 0;
        }
    }
    max_sum
}

fn main() {
    let nums = vec![-2, 1, -3, 4, -1, 2, 1, -5, 4];
    println!("{}", max_sub_array(&nums));
    let nums = vec![1];
    println!("{}", max_sub_array(&nums));
    let nums = vec![5,4,-1,7,8];
    println!("{}", max_sub_array(&nums));
}

输出：

6
1
23

---

54. 螺旋矩阵 Spiral Matrix

给你一个 m 行 n 列的矩阵 matrix ，请按照 顺时针螺旋顺序 ，返回矩阵中的所有元素。

示例 1：

输入：matrix = [[1,2,3],[4,5,6],[7,8,9]]
输出：[1,2,3,6,9,8,7,4,5]

示例 2：

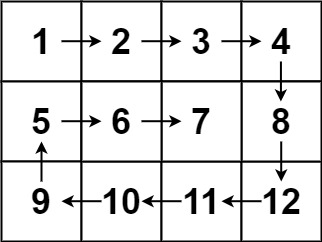
输入：matrix = [[1,2,3,4],[5,6,7,8],[9,10,11,12]]
输出：[1,2,3,4,8,12,11,10,9,5,6,7]

提示：

• m == matrix.length
• n == matrix[i].length
• 1 <= m, n <= 10
• -100 <= matrix[i][j] <= 100

代码1：

fn spiral_order(matrix: &[Vec<i32>]) -> Vec<i32> {
    if matrix.is_empty() {
        return vec![];
    }
    let (m, n) = (matrix.len(), matrix[0].len());
    let mut res = vec![0; m * n];
    let (mut top, mut bottom, mut left, mut right) = (0, m - 1, 0, n - 1);
    let mut idx = 0;
    while top <= bottom && left <= right {
        for i in left..=right {
            res[idx] = matrix[top][i];
            idx += 1;
        }
        for i in top + 1..=bottom {
            res[idx] = matrix[i][right];
            idx += 1;
        }
        if top < bottom && left < right {
            for i in (left..right).rev() {
                res[idx] = matrix[bottom][i];
                idx += 1;
            }
            for i in (top + 1..=bottom - 1).rev() {
                res[idx] = matrix[i][left];
                idx += 1;
            }
        }
        top += 1;
        bottom -= 1;
        left += 1;
        right -= 1;
    }
    res
}

fn main() {
    let matrix = vec![
        vec![1, 2, 3],
        vec![4, 5, 6],
        vec![7, 8, 9],
    ];
    println!("{:?}", spiral_order(&matrix));
    let matrix = vec![
        vec![1, 2, 3, 4],
        vec![5, 6, 7, 8],
        vec![9,10,11,12],
    ];
    println!("{:?}", spiral_order(&matrix));
}

代码2： 递归

fn spiral_order(matrix: Vec<Vec<i32>>) -> Vec<i32> {
    fn spiral_helper(top: usize, bottom: usize, left: usize, right: usize, res: &mut Vec<i32>, idx: &mut usize, matrix: &Vec<Vec<i32>>) {
        if top > bottom || left > right {
            return;
        }
        
        // 从左到右遍历上边界
        for i in left..=right {
            res[*idx] = matrix[top][i];
            *idx += 1;
        }
        
        // 从上到下遍历右边界
        for i in (top + 1)..=bottom {
            res[*idx] = matrix[i][right];
            *idx += 1;
        }
        
        if top < bottom && left < right {
            // 从右到左遍历下边界
            for i in (left..right).rev() {
                res[*idx] = matrix[bottom][i];
                *idx += 1;
            }
            
            // 从下到上遍历左边界
            for i in ((top + 1)..bottom).rev() {
                res[*idx] = matrix[i][left];
                *idx += 1;
            }
        }
        
        // 矩形边界变小，递归调用spiral_helper继续遍历
        spiral_helper(top + 1, bottom - 1, left + 1, right - 1, res, idx, matrix);
        
    }
    
    let m = matrix.len();
    let n = matrix[0].len();
    let mut res = vec![0; m * n]; // 用于记录遍历结果
    let mut idx = 0; // 当前结果数组的下标
    
    // 从矩形最外层开始遍历
    spiral_helper(0, m - 1, 0, n - 1, &mut res, &mut idx, &matrix);
    
    res
}

fn main() {
    let matrix = vec![
        vec![1, 2, 3],
        vec![4, 5, 6],
        vec![7, 8, 9],
    ];
    println!("{:?}", spiral_order(matrix));
    
    let matrix = vec![
        vec![1, 2, 3, 4],
        vec![5, 6, 7, 8],
        vec![9,10,11,12],
    ];
    println!("{:?}", spiral_order(matrix));
}

输出：

[1, 2, 3, 6, 9, 8, 7, 4, 5]
[1, 2, 3, 4, 8, 12, 11, 10, 9, 5, 6, 7] 

---

🌟 每日一练刷题专栏 🌟

✨ 持续，努力奋斗做强刷题搬运工！

👍 点赞，你的认可是我坚持的动力！ 

🌟 收藏，你的青睐是我努力的方向！ 

✎ 评论，你的意见是我进步的财富！  

☸ 主页：https://hannyang.blog.csdn.net/

	Rust每日一练 专栏 （2023.5.16~）更新中...
	Golang每日一练 专栏 （2023.3.11~）更新中...
	Python每日一练 专栏 （2023.2.18~2023.5.18）暂停更
	C/C++每日一练 专栏 （2023.2.18~2023.5.18）暂停更
	Java每日一练 专栏 （2023.3.11~2023.5.18）暂停更