文章目录
- 一.课题概述
- 1.问题
- 2.分析
- 3.目标
- 二.图的实现
- 1.图的存储结构
- 2.图的基本操作
- 2.1添加顶点
- 2.2添加边弧
- 2.3Kruskal算法
- 2.4Prim算法
- 三.堆的实现
- 1.堆的概念及结构
- 2.堆的基本操作
- 2.1入堆(向上调整算法)
- 2.2出堆(向下调整算法)
- 四.位图的实现
- 1.位图的实现原理
- 2.位图的基本操作
- 2.1将某位置设置为1
- 2.2将某位置设置为0
- 2.3判断某位置是1还是0
- 五.并查集的实现
- 1.并查集的概念及原理
- 2.并查集的基本操作
- 2.1查找元素属于哪个集合(即找该集合的根结点)
- 2.2判断两个元素是否属于同一个集合
- 2.3将两个集合归并成一个新集合
- 2.4获取并查集(森林)中集合(树)的个数
- 六.红黑树的实现
- 1.红黑树的性质及结构
- 1.1性质
- 1.2结构
- 2.红黑树的基本操作
- 2.1插入
- 2.2删除
- 2.3查找
- 七.程序演示
- 1.程序的操作
- 1.1添加顶点
- 1.2添加边弧
- 1.3删除顶点
- 1.4删除边弧
- 1.5打印图形
- 1.6最小生成树
- 1.7BFS
- 1.8DFS
- 2.程序的测试
- 八.课设总结
- 九.源代码
- 1.Test.cxx
- 2.Graph.hpp
- 3.Heap.hpp
- 4.BitMap.hpp
- 5.UnionFindSet.hpp
- 6.RedBlackTree.hpp
一.课题概述
1.问题
假定有这么一个问题,有11个城市,城市之间有一些天然气管道,铺设天然气管道需要花费不同的金额,现在要你选择其中一些天然气管道,使得所有城市可以互相联通且花费最小。

2.分析
我们把这个问题抽象为一张图,每个城市是一个顶点,城市与城市之间的管道是一条无向边,城市之间铺设天然气管道的花费为无向边的权值。从而将这个问题转换为图的最小生成树问题,构造最小生成树的方法有:Kruskal算法和Prim算法。
最小生成树: 在加权连通图的所有生成树中,各边权值之和最小的生成树,称为最小生成树.
- 该定义是在无向连通图的基础上的
- 最小生成树可能不唯一,但是其权值之和是唯一的
- 对于n个结点的图,其生成树中必定有n-1条边(对于上述问题只需选出10条天然气管道即可,并且不构成环)
MST性质: 假设G=(V,E)是一个加权连通图,U是顶点集V的一个非空子集.若(u,v)是一条具有最小权值的边,其中u属于U,v属于V-U,则必存在一棵包含边(u,v)的最小生成树.
3.目标
通过实现图的数据结构,把这11个城市当成顶点加入到图中,并将对应的城市之间的管道看成顶点之间的边并赋予权值添加到图中,通过实现Kruskal算法和Prim算法求出最小生成树,从而解决上述问题.
二.图的实现
1.图的存储结构
因为图中既有顶点,又有边弧(顶点与顶点之间的关系),因此,在图的存储中,只需要保存顶点和边弧的关系即可。对于顶点来说,保存比较简单,只需要用一维数组来保存即可。那边的关系该如何保存呢?
- 邻接矩阵 :用nxn的二维数组(矩阵)来表示顶点间的邻接关系。
- 邻接表 :将顶点的顺序存储结构和各顶点的邻接点的链式存储结构相结合的存储方式。

因为Kruskal算法和Prim算法需要通过边的权值和是否构成环这样的条件来选取最小生成树的边,而邻接矩阵能通过两个顶点的下标在O(1)的时间判断两个顶点的连接关系,并取到权值,所以本次课设采用邻接矩阵来表示图中顶点与顶点之间的关系。
最后还有一个问题:如果获取某顶点在邻接矩阵的下标???
-
将存储顶点的一维数组遍历一遍:时间复杂度O(n)
-
将顶点和对应的下标存储在红黑树(平衡二叉树)中:时间复杂度O(log2n)
-
将顶点和对应的下标存储在哈希表中:时间复杂度O(1)
使用第一种方案时间效率低下,使用第三种方案虽然时间效率很高,但是所需空间过大,因为我们采用的邻接矩阵的空间开销已经很大了,所以选择采用第二种方案来进行获取某顶点在邻接矩阵的下标。
template<class V,class W=int,W W_MAX=INT_MAX,bool Directed=false>
class Graph
{
private:
std::vector<V> _vertexs; // 顶点集合,下标找顶点
std::vector<vector<W>> _matrix; // 邻接矩阵,顶点与顶点之间的权值
YX::RedBlackTree<V, int> _findIndexTree; // 顶点与下标的映射,顶点找下标
}
2.图的基本操作
2.1添加顶点
思路:先判断添加的顶点在不在,如果顶点已经存在图中则不需要再添加。反之则将顶点插入到vertexs数组中,并将该顶点与对应的下标插入findIndexTree红黑树中,最后matrix邻接矩阵当前的每一行添加一列,再给matrix邻接矩阵增加一行。
bool AddVertex(const V& v) // 添加顶点
{
int vi = FindVertexIndex(v); // 找该顶点对应的下标,不存在则为-1
if (vi != -1) // 顶点已经存在,无需再添加
return false;
_vertexs.push_back(v);
_findIndexTree.Insert(make_pair(v, (int)_vertexs.size() - 1));
for (size_t i = 0; i < _matrix.size(); i++) // 每一行添加一列
{
_matrix[i].push_back(W_MAX);
}
_matrix.push_back(vector<W>(_matrix.size() + 1, W_MAX)); // 添加一行
return true;
}
2.2添加边弧
思路:先输入一个起始顶点,再输入一个终止顶点,最后输入两个顶点之间的权值。如果输入的这两个顶点都在图中,则在对应的matrix邻接矩阵位置赋对应的权值。(如果两个顶点之间不相连,则对应的权值为int的最大值)
bool AddEdge(const V& src, const V& dst,const W& w) // 添加边
{
int srci = FindVertexIndex(src);
int dsti = FindVertexIndex(dst);
if (srci == -1 || dsti == -1)
return false;
_matrix[srci][dsti] = w;
if (!Directed) // 如果为无向图,再添加dst到src的边
{
_matrix[dsti][srci] = w;
}
return true;
}
2.3Kruskal算法
使用全局贪心思想,从剩下的边中选择具有最小权值且不会产生回路的边加入到生成树的边集中.
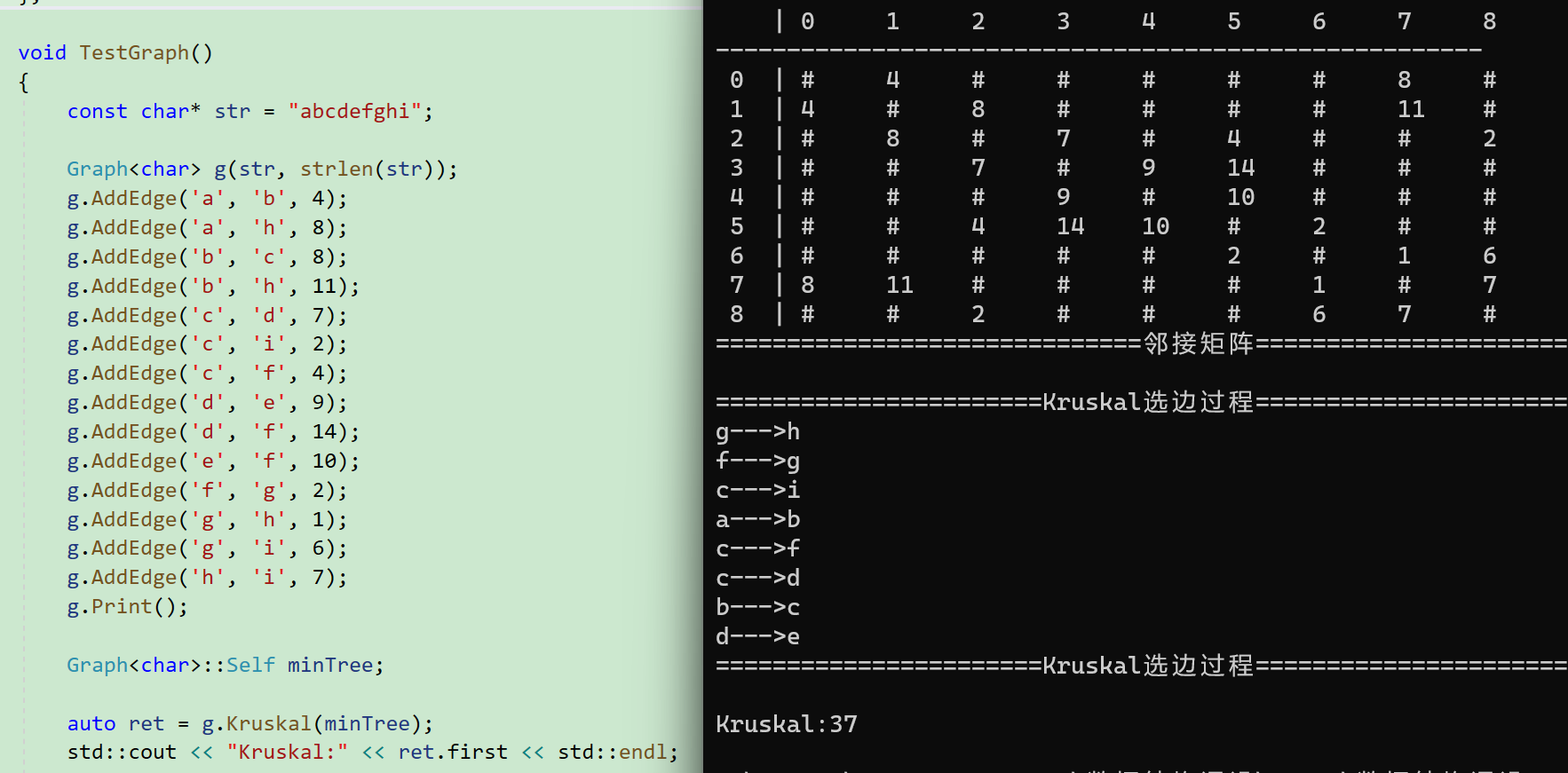
任给一个有n个顶点的连通网络N={V,E}.首先构造一个由这n个顶点组成,不含任何边的图minTree={V,NULL}.其中每一个顶点自成一个连通分量,其次不断从E中取出权值最小的一条边(若有多条任取其中一条), 若该边的两个顶点来自不同的连通分量,则将此边加入到G中。如此重复,直到所有顶点在同一个连通分量上为止。核心:每次迭代时,选出一条具有最小权值,且两端点不在同一连通分量上的边,加入生成树。
 1
1
想要实现Kruskal算法就必须解决掉两个问题:
- 如何选出最小权值的边?
- 如何判断选出的边会不会构成环?
对于第一个问题可以使用堆,建立小根堆将所有的边压入堆中,堆顶即为权值最小的边。
边的结构体类型:
struct Edge
{
int _srci; // 起始顶点的下标
int _dsti; // 终止顶点的下标
W _weight; // 边的权值
Edge() = default;
Edge(const int& srci, const int& dsti, const W& weight)
:_srci(srci)
,_dsti(dsti)
,_weight(weight)
{}
bool operator>(const Edge& e) const
{
return this->_weight > e._weight;
}
bool operator<(const Edge& e) const
{
return this->_weight < e._weight;
}
};
而对于第二个问题需要用到并查集,只有选出边的两个顶点不在同一个集合中才能加入到minTree中,加入minTree之后将这两个顶点合并到一个集合中。
代码实现:
pair<W,bool> Kruskal(Self& minTree)
{
size_t vertexCount = this->_vertexs.size();
minTree._vertexs = this->_vertexs;
minTree._findIndexTree = this->_findIndexTree;
minTree._matrix.resize(vertexCount, vector<W>(vertexCount, W_MAX));
// 将所有的边压入小根堆中
Heap<Edge, std::greater<Edge>> hp;
for (size_t i = 0; i < _matrix.size(); i++)
{
for (size_t j = 0; j < _matrix[i].size(); j++)
{
if (i < j && _matrix[i][j] != W_MAX)
{
hp.Push(Edge(i, j, _matrix[i][j]));
}
}
}
// 创建n棵树的并查集
UnionFindSet ufs(vertexCount);
W retW=W();
size_t minVertexCount = 0;
while (!hp.Empty())
{
// 取出权值最小的边
Edge minEdge = hp.Top();
hp.Pop();
// 如果这两个顶点不在一个集合,则将这条边添加到minTree
if (!ufs.IsInSet(minEdge._srci, minEdge._dsti))
{
cout << minTree._vertexs[minEdge._srci] << "--->" << minTree._vertexs[minEdge._dsti] << std::endl;
Sleep(1000);
minTree.AddEdge(minTree._vertexs[minEdge._srci], minTree._vertexs[minEdge._dsti], minEdge._weight);
// 再将这两个顶点合并成一个集合
ufs.Union(minEdge._srci, minEdge._dsti);
retW += minEdge._weight;
minVertexCount++;
}
if (minVertexCount == vertexCount - 1)
{
break;
}
}
if (minVertexCount == vertexCount - 1) // 只有选出n-1条边,最小生成树才构造成功
{
return make_pair(retW, true);
}
else
{
return make_pair(W(), false);
}
}
Kruskal算法的验证:
2.4Prim算法
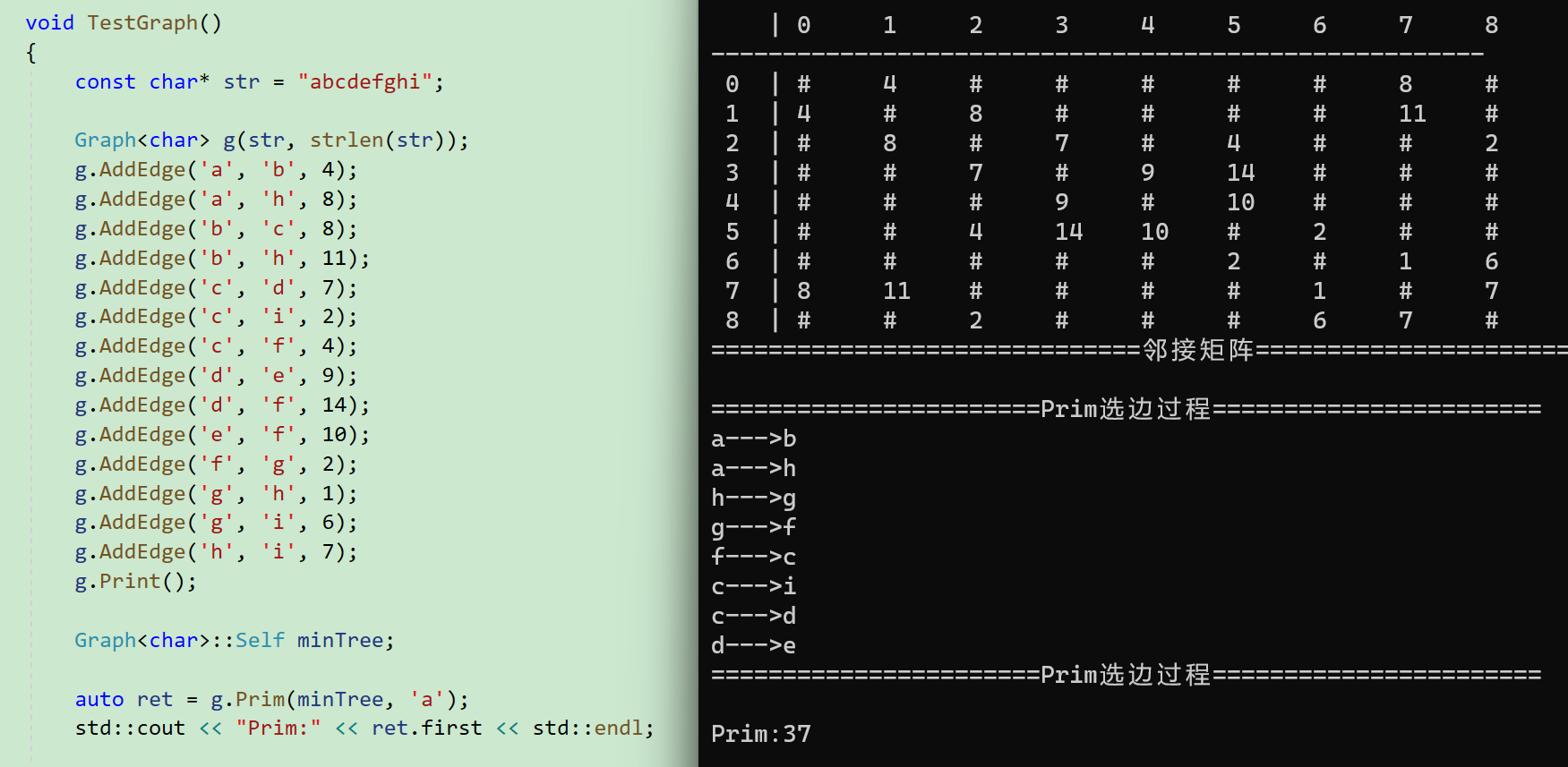
设G=(V,E)是一个连通的带权图,其中V是顶点的集合,E是边的集合,TE为最小生成树的集合。则Prim算法通过以下步骤得到最小生成树:
- 最小生成树T的初始状态为U={u0}(u0∈V),TE={nullptr},此时图中只有一个起始起点,边集为空。
- 在所有u∈U,v∈V-U的边中找一条代价最小的边(u,v);把边(u,v)并入生成树的边集TE,同时v并入生成树的顶点集U。
- 重复执行步骤2,直至U=V为止。此时,TE中必有n-1条边,T=(U,TE)为G的最小生成树。
 2
2
想要实现Prim算法同样要解决掉两个问题(设已选出的顶点集合为X,未选出的顶点集合为Y):
- 如何选出从X集合的顶点到Y集合的顶点构成权值最小的边?
- 如何区分X集合的顶点与Y集合的顶点?
我们知道Prim算法的执行需要给出某顶点为源点来开始执行。所以我们可以将每次加入X集合的顶点相连的边加入小根堆中。只有权值最小的边并且起始顶点在X中,终止顶点在Y中才可以加入生成树。加入完成之后将该Y集合的顶点变为X集合的顶点,并且将该顶点与之相连的边继续加入小根堆中。
对于如何区分X与Y集合,我们可以用位图来标识,因为我们知道顶点的下标,通过开出对应数量的标识位,用顶点的下标来判断是X集合还是Y集合,如果对应的顶点下标为1则为X集合,为0则为Y集合。
代码实现:
pair<W, bool> Prim(Self& minTree, const V& src) // 局部贪心算法
{
int srci = FindVertexIndex(src);
if (srci == -1)
return make_pair(W(), false);
size_t vertexCount = this->_vertexs.size();
minTree._vertexs = this->_vertexs;
minTree._findIndexTree = this->_findIndexTree;
minTree._matrix.resize(vertexCount, vector<W>(vertexCount, W_MAX));
Heap<Edge, std::greater<Edge>> hp;
// 用位图标记已选的顶点X集合和未选的顶点Y集合 X:1 Y:0
BitMap XY(vertexCount);
XY.Set(srci);
for (size_t i = 0; i < _matrix[srci].size(); i++)
{
// 将与src相连的顶点对应的边入堆
if (_matrix[srci][i] != W_MAX && XY[srci] && !XY[i])
{
hp.Push(Edge(srci, i, _matrix[srci][i]));
}
}
W retW = W();
size_t minVertexCount = 0;
while (!hp.Empty())
{
Edge minEdge = hp.Top();
hp.Pop();
if (XY[minEdge._srci] && !XY[minEdge._dsti])
{
cout << minTree._vertexs[minEdge._srci] << "--->" << minTree._vertexs[minEdge._dsti] << std::endl;
Sleep(1000);
// 只有srci在X集合,dsti在Y集合,才能加入到minTree
minTree.AddEdge(minTree._vertexs[minEdge._srci], minTree._vertexs[minEdge._dsti], minEdge._weight);
XY.Set(minEdge._dsti);
for (size_t i = 0; i < _matrix[minEdge._dsti].size(); i++)
{
// 将与dsti相连的顶点对应的边入堆
if (_matrix[minEdge._dsti][i] != W_MAX && XY[minEdge._dsti] && !XY[i])
{
hp.Push(Edge(minEdge._dsti, i, _matrix[minEdge._dsti][i]));
}
}
retW += minEdge._weight;
minVertexCount++;
}
if (minVertexCount == vertexCount - 1)
{
break;
}
}
if (minVertexCount == vertexCount - 1)
{
return make_pair(retW, true);
}
else
{
return make_pair(W(), false);
}
}
Prim算法的验证(从顶点a开始选边):
三.堆的实现
1.堆的概念及结构
- 堆是一种数据结构,它与操作系统的虚拟进程地址空间中的堆是两回事。堆的逻辑结构是一颗特殊的完全二叉树,它要求双亲结点中的数据要大于或者小于其左右孩子结点中的数据;而堆的物理结构是由动态数组来实现的。
- 堆可以分为大根堆与小根堆。设数组a存储着堆中的数据,大根堆就是双亲结点的数据大于其左右孩子结点的数据(a i >= a ~2i + 1~ && a i >= a ~2i + 2~);小根堆就是双亲结点的数据小于其左右孩子结点的数据(a i <= a ~2i + 1~ && a i <= a ~2i + 2~)。
- 根据堆的性质我们可以知道,在大根堆中根结点的数据值是最大的,而在小根堆中根结点的数据值是最小的。

堆的成员变量(本次堆的实现采用适配器模式,复用stl中的vector,通过类模板的实例化来控制大小堆):
// 默认大堆
template<typename T,typename Compare=less<T>,typename Container=vector<T>>
class Heap
{
private:
Container _con; // 容器
Compare _com; // 仿函数
}
2.堆的基本操作
堆的核心操作主要有两点:
- 入堆的向上调整
- 出堆的向下调整
2.1入堆(向上调整算法)
入堆的操作就是先将数据插入到数组最后一个位置上,数据插入完成后再进行向上调整。向上调整的基本思路就是让插入的数据与其双亲结点的数据进行比较,如果插入的数据比其双亲结点的数据大,则将插入的数据与双亲数据交换,直到有双亲数据比插入数据大或者插入数据已经换到根结点就停止。

代码实现:
// 向上调整
void AdjustUp(int child)
{
int parent = (child - 1) / 2;
while (child > 0)
{
if (this->_com(this->_con[parent], this->_con[child]))
{
std::swap(this->_con[child], this->_con[parent]);
child = parent;
parent = (child - 1) / 2;
}
else
{
break;
}
}
}
void Push(const T& val)
{
// 入堆,插入到vector最后,然后从最后一个元素开始进行向上调整
this->_con.push_back(val);
this->AdjustUp(this->_con.size() - 1);
}
2.2出堆(向下调整算法)
出堆的操作不能直接将根结点的数据删除,否则会把数据打乱,造成堆不再是大根堆,而且再次调整成大根堆的代价很大。正确的出堆操作是将根结点的数据与数组中最后一个结点的数据进行交换,然后将换上来的结点数据与其左右孩子进行调整直到大根堆复原。向下调整的基本思路是先选出左右孩子中数据大的那一个结点(小根堆就是选出小的那一个结点),再将数据大的那一个结点与其双亲结点比较,如果选出来的那一个数据大的孩子结点比双亲结点的数据大则进行交换,直到换上来的结点成了叶子结点或者选出的那一个孩子结点比换上来的结点小就停止交换。
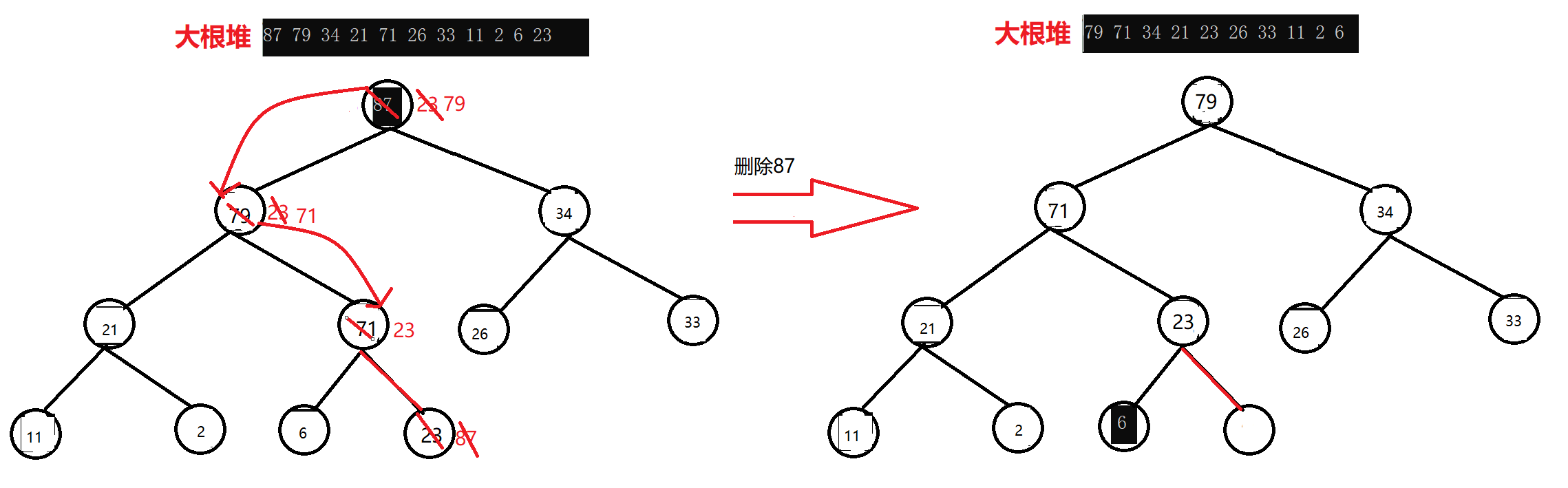
代码实现:
// 向下调整
void AdjustDown(int parent)
{
int child = 2 * parent + 1;
while (child < (int)this->_con.size())
{
if (child + 1 < (int)_con.size() && _com(_con[child], _con[child+1]))
{
child++;
}
if (this->_com(this->_con[parent], this->_con[child]))
{
std::swap(this->_con[child], this->_con[parent]);
parent = child;
child = 2 * parent + 1;
}
else
{
break;
}
}
}
void Pop()
{
if (this->_con.empty())
{
perror("Heap::Pop");
return;
}
// 出堆,堆顶元素与最后一个元素交换,再从堆顶开始进行向下调整
std::swap(this->_con[0], this->_con[this->_con.size() - 1]);
this->_con.pop_back();
this->AdjustDown(0);
}
四.位图的实现
1.位图的实现原理
查找一个数是否存在,其实答案就是存在或者不存在,这种只需要回答是与否的问题,我们都可以用二进制中的比特位来表示,1表示该数存在,反之0表示该数不存在,因此位图中的每个数据单元都是一个bit位。但在常见的编程语言中,我们能操作的最小空间是一字节,那我们该如何进行比特位的操作呢?答案是位运算。
- &:在按位与时,有0就变0,没有0就变1。
- |:在按位或时,有1就变1,没有就变0。
- ^:进行按位异否时,相同变0,不相同变1。
- <<:左边抛弃、右边补0。0000 0001 -> 0000 0010
- >> :a.逻辑移位(左边用0填充,右边丢弃),b. 算术移位(左边用原该值的符号位填充,右边丢弃)。
- ~:按位取反。0001 -> 1110

如果需要将第10(下标为9)个位置的比特位置为1,则需要先算出该位置所在的区间,再算出在该区间的下标位置。上述操作需要用到 / 与**%** ,然后再用一系列的位运算即可。
位图的成员变量与构造函数
class BitMap
{
private:
std::vector<char> _bitMap; // 每一个区间有8个比特位
public:
BitMap(size_t N)
:_bitMap(N/sizeof(char)+1,0) // 根据需要多少个比特位,开辟多少个char
{}
}
2.位图的基本操作
2.1将某位置设置为1
- index/8:计算在哪一个区间
- index%8:计算在区间的哪一个位置
- _bitMap[group] |= (1 << groupIndex):将对应的位置变为1
void Set(size_t index) // 改为真
{
size_t group = index / 8;
size_t groupIndex = index % 8;
this->_bitMap[group] |= (1 << groupIndex);
}
2.2将某位置设置为0
- index/8:计算在哪一个区间
- index%8:计算在区间的哪一个位置
- _bitMap[group] &= (~(1 << groupIndex)):将对应比特位变为0
void ReSet(size_t index) // 改为假
{
size_t group = index / 8;
size_t groupIndex = index % 8;
this->_bitMap[group] &= (~(1 << groupIndex));
}
2.3判断某位置是1还是0
如果对应的比特位为1返回true,否则返回false。
bool Test(size_t index) // 判断对应下标真假
{
size_t group = index / 8;
size_t groupIndex = index % 8;
size_t ret = (this->_bitMap[group] & (1 << groupIndex));
return !(ret == 0);
}
// [ ]运算符重载
bool operator[](size_t index)
{
return this->Test(index);
}
五.并查集的实现
1.并查集的概念及原理
在一些应用问题中,需要将n个不同的元素划分成一些不相交的集合。开始时,每一个元素自成一个单元素的集合,然后按照某些关系将一些集合合并成一个新集合。在此过程中要反复用到查询某一个元素是否归属于该集合的运算的数据结构称为并查集。
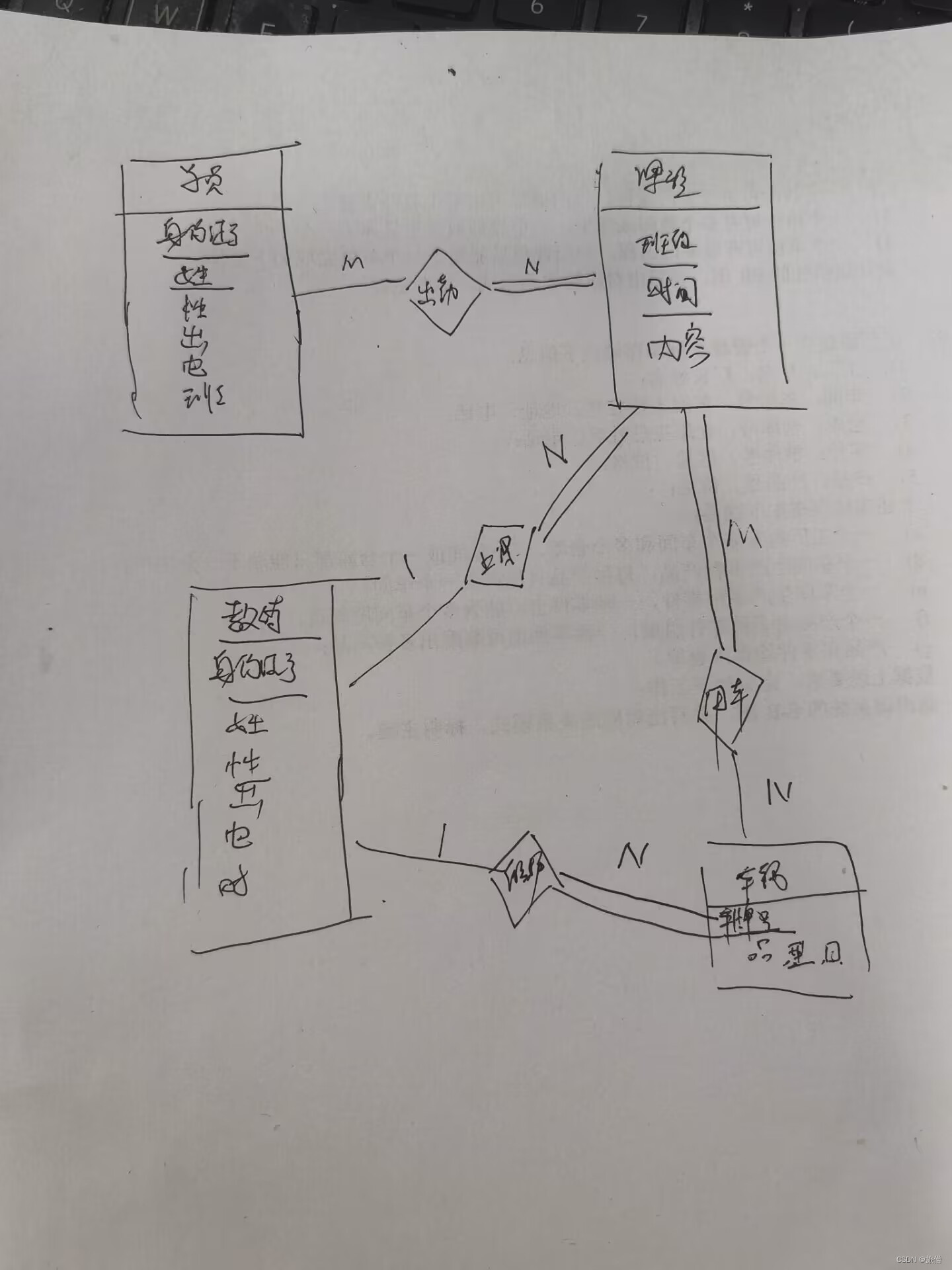
值得注意的是并查集是一片森林,每一个集合相当一棵树。每一个元素通过编号,存储在一维数组中,采用双亲表示法,即每一个元素记录自己双亲所在数组中的下标,而根结点比较特殊,记录的下标数为负数,该负数的绝对值表示该集合元素的个数。
例如:一个新班级中有10名新学生(依次编号0~9),刚开始他们谁都不认识谁,各自成一个单元素的集合,记录的下标数都为-1。
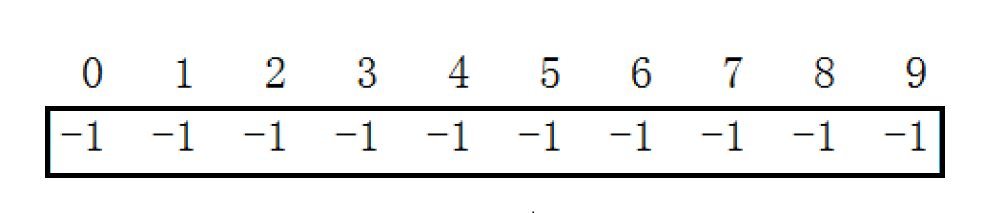
经过分寝安排,在同一个寝室的学生慢慢互相认识,互相熟悉,成为了一个新的集合(朋友圈)。

从上图可知:编号0,6,7,8为一个集合;1,4,9为一个集合;2,3,5为一个集合。其中0,1,2为对应集合的根(即寝室长)。
- 数组的下标对应集合中元素的编号
- 数组中如果为负数,负号代表根,数字代表该集合中元素个数
- 数组中如果为非负数,代表该元素双亲在数组中的下标
经过一段校园生活,1号同学与8号同学互相认识了,两个寝室的学生互相介绍,最后成为了一个新的集合。

并查集的成员变量:
template<class T>
class UnionFindSet
{
private:
std::vector<int> _ufs; // 双亲表示法
std::vector<T> _valArr; // 下标映射值
std::map<T, int> _indexMap; // 值映射下标
};
因为本次实现并查集是为了解决Kruskal算法选边时不构成环,我们可以通过图的成员变量知道顶点的编号,所以我们可以简化并查集的成员变量:
class UnionFindSet
{
private:
std::vector<int> _ufs; // 一维数组
public:
UnionFindSet(size_t n) // 初始时,为n个单元素的集合
:_ufs(n,-1)
{}
}
2.并查集的基本操作
2.1查找元素属于哪个集合(即找该集合的根结点)
如果某元素存储的下标为负数,该元素即为根结点。
int FindRootIndex(int x) // 找根结点的下标
{
int root = x;
while (this->_ufs[root] >= 0)
{
root = this->_ufs[root];
}
return root;
}
2.2判断两个元素是否属于同一个集合
判断两个元素的根结点下标是否相同,相同即为同一个集合。
bool IsInSet(int x1, int x2) // 判断在不在一个集合
{
int root1 = FindRootIndex(x1);
int root2 = FindRootIndex(x2);
return root1 == root2;
}
2.3将两个集合归并成一个新集合
先找出两个集合对应的根结点,再进行合并。
bool Union(int x1, int x2) // 两个集合合并
{
int root1 = FindRootIndex(x1);
int root2 = FindRootIndex(x2);
if (root1 == root2) // 已经在一个集合,不需要合并
return false;
// x2合并到x1中
this->_ufs[root1] += this->_ufs[root2]; // x1集合先加上x2集合元素的个数
this->_ufs[root2] = root1; // x2集合的根结点再记录x1集合的根结点下标
return true;
}
2.4获取并查集(森林)中集合(树)的个数
遍历数组,数组中元素为负数的个数即为集合的个数。
std::size_t SetCount() // 集合的个数
{
std::size_t count = 0;
for (auto& e : this->_ufs)
{
if (e < 0)
count++;
}
return count;
}
六.红黑树的实现
1.红黑树的性质及结构
1.1性质
红黑树也是一种平衡二叉树,在红黑树中每个结点存储着对应的颜色(红色或者黑色),由于AVL树的高度平衡是因为非常频繁地调用旋转来保存自身平衡的,代价较大。所以在AVL树的基础上进一步放宽条件,引入红黑树,即红黑树的最长路径不会比最短路径长两倍。

一棵红黑树需要满足以下性质才能保证最长路径不会超过最短路径的两倍:
- 根结点必须是黑色,其他结点不是黑色就是红色。
- 红色结点的双亲结点与孩子结点都是黑色的,也就是不会存在两个相邻的红色结点。
- 对于每一个结点,从该结点到任一叶结点的路径上,每条路径上的黑色结点数量相同。
- 空结点为黑色。
通过上面的性质可以得出一些结论:
- 最短路径上的结点都是黑色的,而最长路径上的结点一黑一红交替。
- 若一棵红黑树有n个结点则红黑树的高度为h <= 2*log(2) (n+1)。
- 在红黑树中,对于红色结点其出度只能为0或者2。
- 在红黑树中,如果黑色结点只有一个孩子结点,则该孩子结点只能为红色。
1.2结构
红黑树的链式结构采用用三叉链,以便进行旋转。红黑树的每一个结点都存储着左孩子结点地址,右孩子结点地址,双亲结点地址,KeyValue数据以及结点的颜色。
// 枚举类型,标识结点的颜色
enum class Colour
{
RED,
BLACK,
};
template<typename K, typename V>
struct RedBlackTreeNode // 红黑树的结点类型
{
// 三叉链
struct RedBlackTreeNode<K, V>* _left;
struct RedBlackTreeNode<K, V>* _right;
struct RedBlackTreeNode<K, V>* _parent;
// 结点颜色
Colour _colour;
// Key-Value 索引
pair<K, V> _kv;
RedBlackTreeNode(const pair<K, V>& kv)
:_left(nullptr)
, _right(nullptr)
, _parent(nullptr)
, _colour(Colour::RED)
, _kv(kv)
{}
};
template<class K, class V>
class RedBlackTree // 红黑树
{
typedef RedBlackTreeNode<K, V> Node;
private:
Node* _root = nullptr;
}
最后在实现红黑树之前,还要思考一个问题:新插入的结点是红色好还是黑色好?
新开辟的结点默认选择是红色的:假设新插入的结点默认是黑色的,那么这个结点所在的路径会比其他路径多一个黑色的结点,会破坏性质3,调整起来很麻烦。如果插入的结点默认是红色的,所有路径上的黑色结点数量依然相同,如果插入结点的双亲是黑色的则不需要处理直接结束插入,如果插入结点的双亲是红色的则破坏性质2需要处理。所以选择新插入的结点为红色的代价小。
2.红黑树的基本操作
2.1插入
红黑树的插入思路与二叉搜索树的插入相同,只不过红黑树需要在插入新结点之后,判断插入之后有没有违反红黑树的性质。如果没有违反则插入成功,否则需要进行修复使之平衡。
第一步:找到新结点的插入位置,并记录新结点的双亲位置
**第二步:进行插入,如果新结点小于双亲则往左插入,如果新结点大于双亲则往右插入 **
pair<Node*, bool> Insert(const pair<K, V>& kv) // 插入
{
if (_root == nullptr) // 没有结点直接插入
{
_root = new Node(kv);
_root->_parent = nullptr;
_root->_colour = Colour::BLACK;
return make_pair(_root, true);
}
Node* prev = nullptr;
Node* curr = _root;
while (curr != nullptr) // 寻找插入的位置
{
if (curr->_kv.first > kv.first) // 小往左走
{
prev = curr;
curr = curr->_left;
}
else if (curr->_kv.first < kv.first) // 大往右走
{
prev = curr;
curr = curr->_right;
}
else // 不允许键值冗余
{
return make_pair(curr, false);
}
}
curr = new Node(kv);
if (prev->_kv.first < kv.first)
{
prev->_right = curr;
}
else if (prev->_kv.first > kv.first)
{
prev->_left = curr;
}
curr->_parent = prev;
_RepairInsert(prev, curr); // 判断满不满足规则,不满足进行修复
_root->_colour = Colour::BLACK; // 根结点变为黑色
return make_pair(curr, true);
}
**第三步:判断是否需要修复,如果双亲结点的颜色为黑色则不需要修复,如果双亲结点的颜色为红色则需要修复 **
当双亲的颜色为红色时,需要进行修复,而修复的方法分为两种,这两种方法是根据其插入结点的叔叔来决定的。
旋转代码:
// 右单旋
void _RightRotate(Node* parent)
{
Node* parentParent = parent->_parent;
Node* subLeft = parent->_left;
Node* subLeftRight = subLeft->_right;
subLeft->_right = parent;
parent->_parent = subLeft;
parent->_left = subLeftRight;
if (subLeftRight != nullptr)
{
subLeftRight->_parent = parent;
}
// parent为根结点特殊处理
if (parent == _root)
{
_root = subLeft;
subLeft->_parent = nullptr;
}
else
{
if (parentParent->_left == parent)
{
parentParent->_left = subLeft;
}
else if (parentParent->_right == parent)
{
parentParent->_right = subLeft;
}
subLeft->_parent = parentParent;
}
}
// 左单旋
void _LeftRotate(Node* parent)
{
Node* parentParent = parent->_parent;
Node* subRight = parent->_right;
Node* subRightLeft = subRight->_left;
subRight->_left = parent;
parent->_parent = subRight;
parent->_right = subRightLeft;
if (subRightLeft != nullptr)
{
subRightLeft->_parent = parent;
}
// parent为根结点特殊处理
if (parent == _root)
{
_root = subRight;
subRight->_parent = nullptr;
}
else
{
if (parentParent->_left == parent)
{
parentParent->_left = subRight;
}
else if (parentParent->_right == parent)
{
parentParent->_right = subRight;
}
subRight->_parent = parentParent;
}
}
- 当叔叔存在并且为红时,进行调色然后继续往上处理------祖父变为红色,双亲与叔叔变为黑色
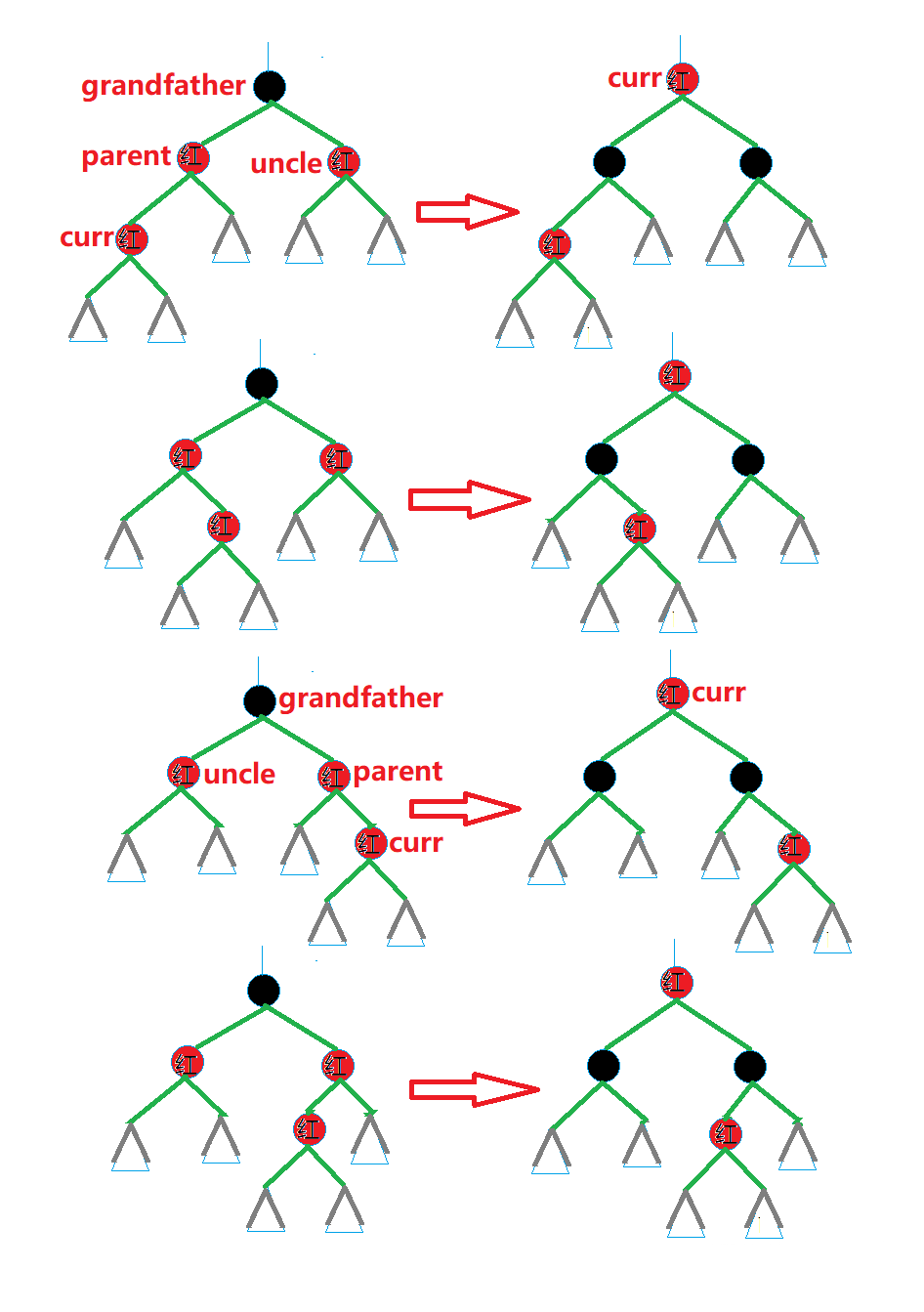
- 当叔叔不存在或者叔叔的颜色为黑,需要进行旋转与调色处理------(1,双亲是祖父的左孩子并且新插入结点是双亲的左孩子,进行祖父右旋转并将祖父变为红,双亲变为黑。(2,双亲是祖父的左孩子并且新插入结点是双亲的右孩子,进行双亲左旋转祖父右旋转,并将祖父变红,新插入结点变黑。(3,双亲是祖父的右孩子并且新插入结点是双亲的右孩子,进行祖父左旋转并将祖父变为红色,双亲变为黑色。(4,双亲是祖父的右孩子并且新插入结点是双亲的左孩子,进行双亲右旋转祖父左旋转,并将祖父变为红色,新插入结点变为黑色。
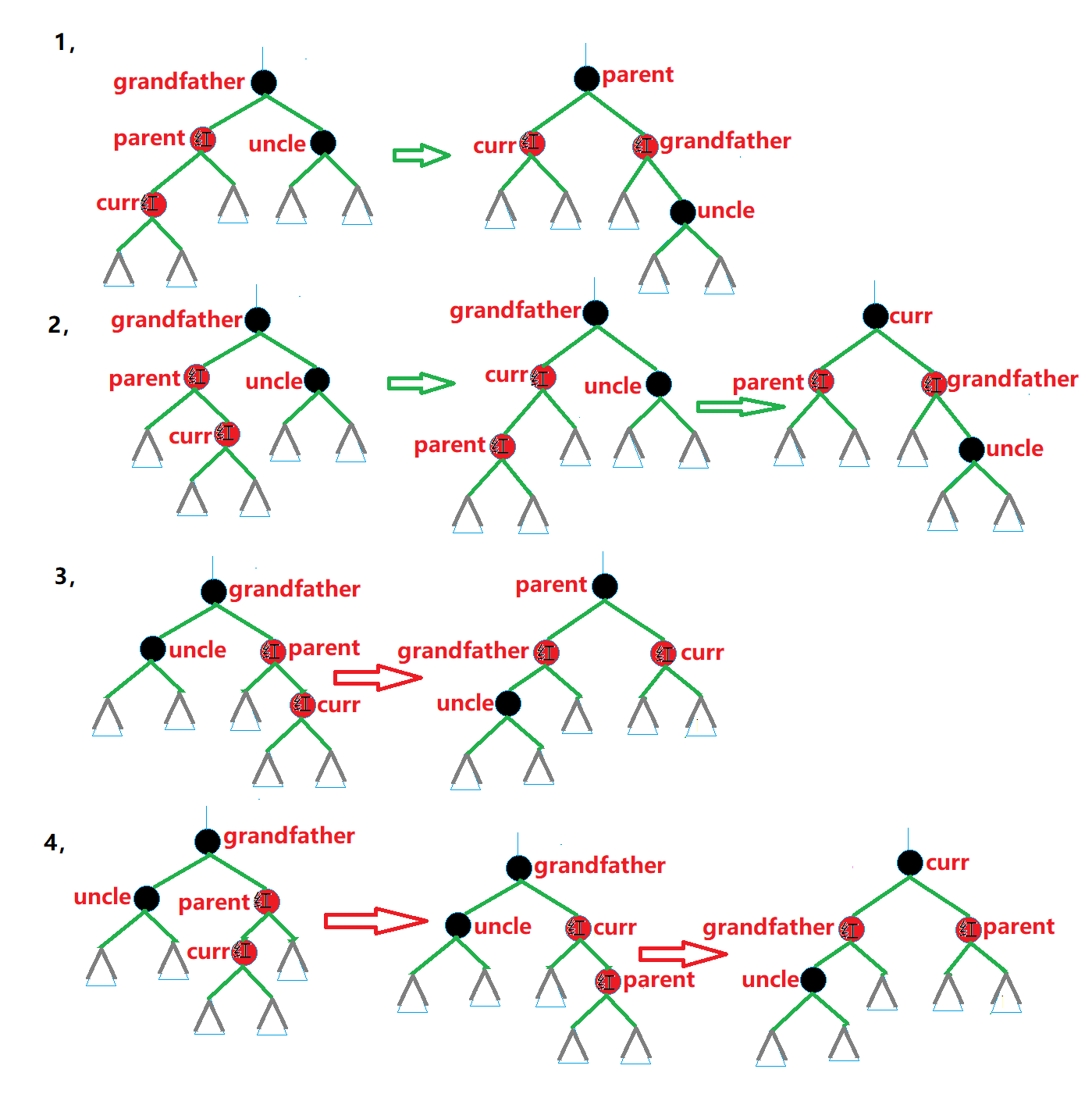
// prev:插入结点的双亲,curr:插入结点
void _RepairInsert(Node* prev, Node* curr)
{
// 因为插入的结点颜色是红色,所以只有当双亲存在且双亲颜色为红才需要修复
while (prev != nullptr && prev->_colour == Colour::RED)
{
// 双亲存在且为红,则祖父一定存在
Node* grandfather = prev->_parent;
if (grandfather->_left == prev)
{
Node* uncle = grandfather->_right;
// 叔叔存在且为红,变色即可
if (uncle != nullptr && uncle->_colour == Colour::RED)
{
prev->_colour = uncle->_colour = Colour::BLACK;
grandfather->_colour = Colour::RED;
}
else // 叔叔不存在或者叔叔存在且为黑,变色加旋转处理
{
if (prev->_left == curr) // 左左---右旋
{
_RightRotate(grandfather);
prev->_colour = Colour::BLACK;
grandfather->_colour = Colour::RED;
}
else if (prev->_right == curr) // 左右---左右双旋
{
_LeftRotate(prev);
_RightRotate(grandfather);
curr->_colour = Colour::BLACK;
grandfather->_colour = Colour::RED;
}
break;
}
}
else if (grandfather->_right == prev)
{
Node* uncle = grandfather->_left;
// 叔叔存在且为红,只需要变色即可
if (uncle != nullptr && uncle->_colour == Colour::RED)
{
prev->_colour = uncle->_colour = Colour::BLACK;
grandfather->_colour = Colour::RED;
}
else // 叔叔不存在或者叔叔存在为黑色,变色加旋转处理
{
if (prev->_right == curr) // 右右---左旋
{
_LeftRotate(grandfather);
grandfather->_colour = Colour::RED;
prev->_colour = Colour::BLACK;
}
else if (prev->_left == curr) // 右左---右左旋
{
_RightRotate(prev);
_LeftRotate(grandfather);
grandfather->_colour = Colour::RED;
curr->_colour = Colour::BLACK;
}
break;
}
}
curr = grandfather;
prev = curr->_parent;
}
}
2.2删除
第一步:找到要删除的结点
第二步:按照要删除结点的类型进行分类删除:1,左子树为空 2,右子树为空 3,左右子树都为空 4,左右子树都不为空------替换删除法
第三步:在删除之前,根据删除结点的特征与颜色进行调整
- 如果删除的结点是红色------可以直接删除,不会影响红黑树的特性。
- 如果删除的结点是黑色,并且有一个孩子结点(孩子结点一定是红色)------则将该黑色结点删除,并将该孩子结点变黑交给双亲托管。
- 如果删除的结点是黑色,并且兄弟结点是黑色,其远侄子是红色------交换双亲与兄弟的颜色,并且将远侄子的颜色变为黑色,双亲进行一次单旋转(删除结点在双亲的左进行左旋转;删除结点在双亲的右进行右旋转);完成之后3特征结束。
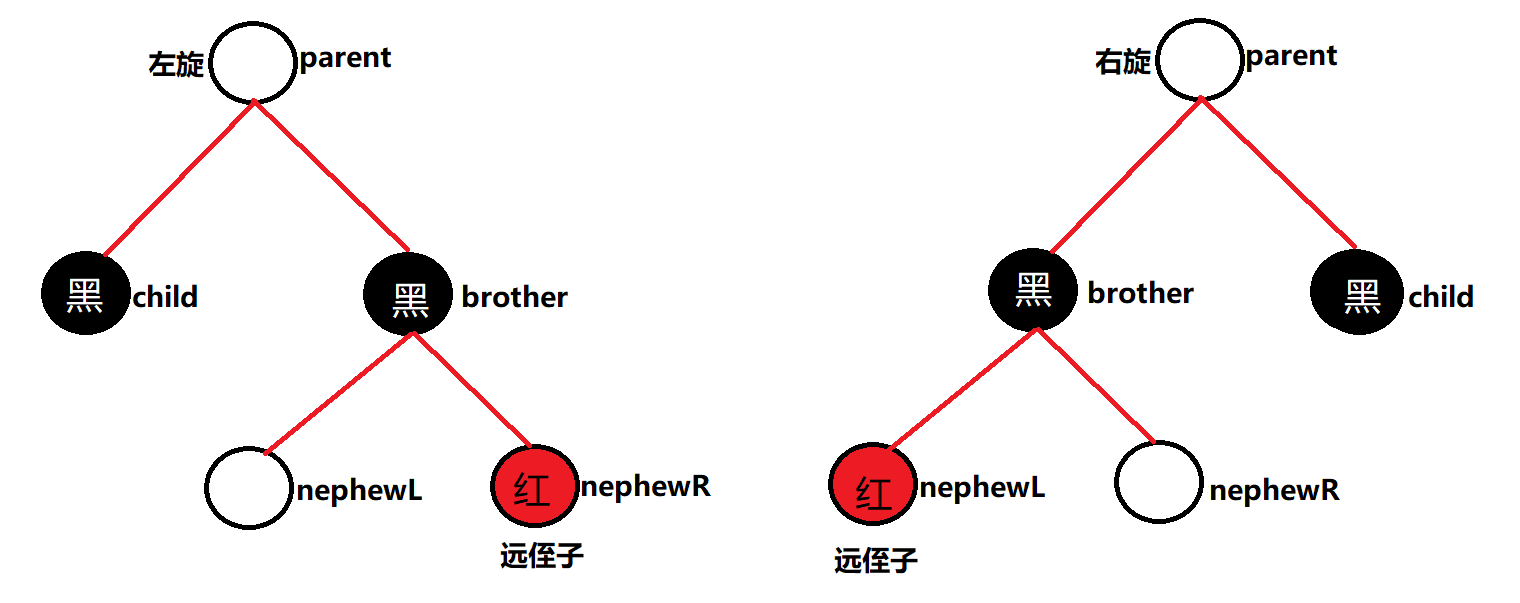
- 如果删除结点是黑色,并且兄弟结点是黑色,近侄子是红色,远侄子是黑色------兄弟与近侄子交换颜色,然后对兄弟做一次单旋转(删除结点在双亲的左进行右旋转;删除结点在双亲的右进行左旋转);完成之后4特征变为3特征继续。
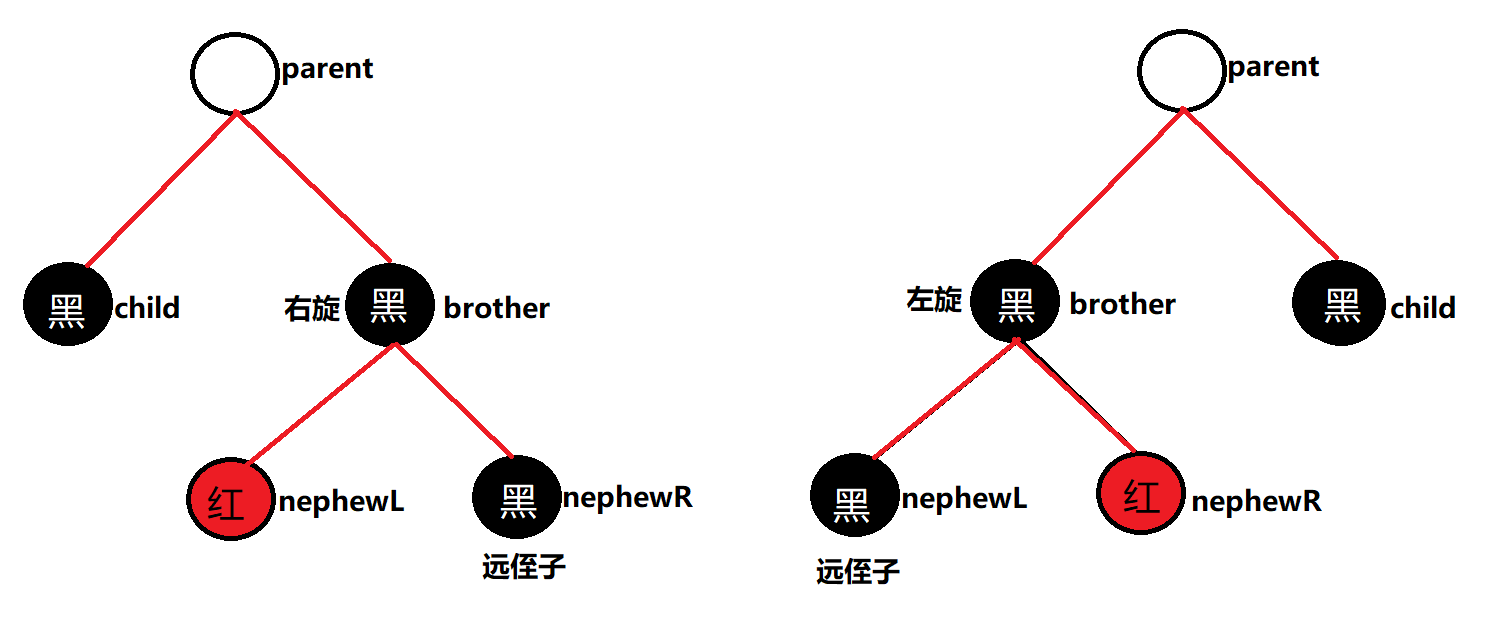
- 如果删除的结点是黑色,并且兄弟结点的颜色是红色------交换双亲与兄弟的颜色,然后对双亲做一次单旋转(删除结点在双亲的左进行左旋转;删除结点在双亲的右进行右旋转)这样完成之后5特征变为3特征或者4特征孩子6特征继续。
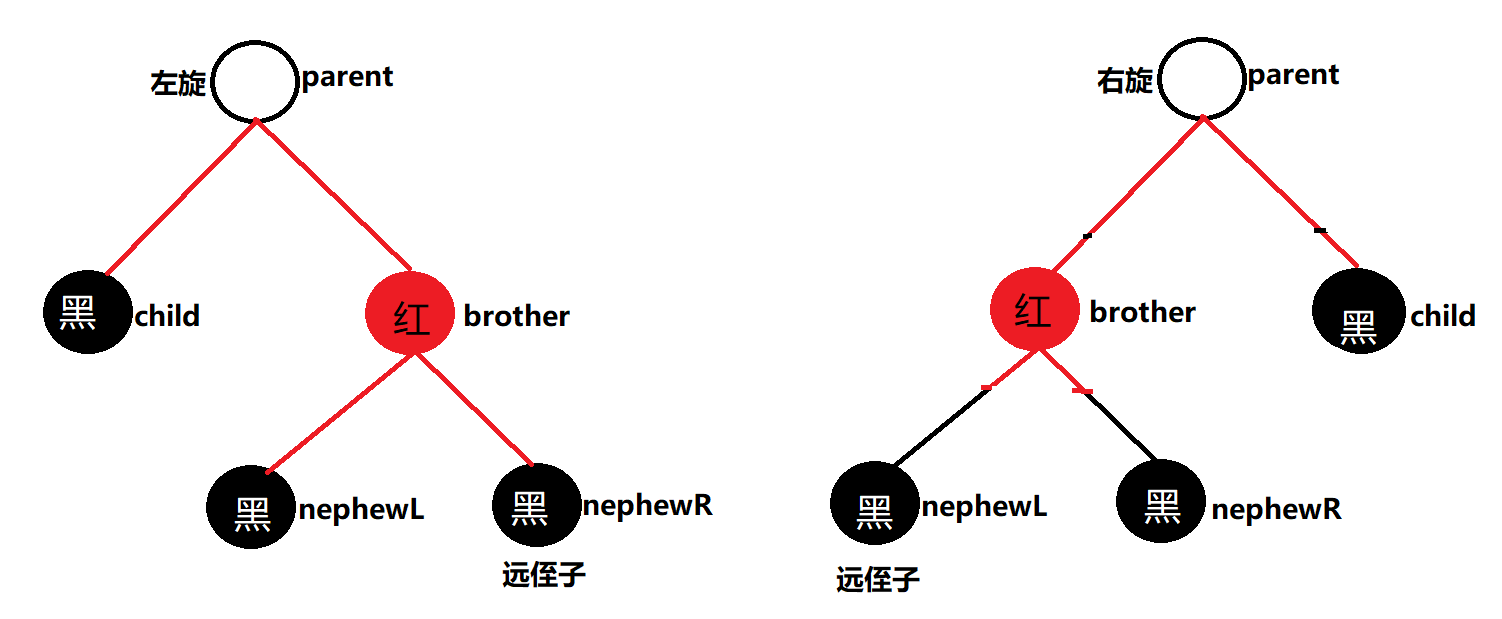
- 如果删除的结点是黑色,兄弟结点是黑色并且其左右孩子都是黑色(左右孩子可以为空)------将兄弟结点变为红色,紧接着判断双亲是否为根结点或者是否为红色,如果成立调整结束,如果不成立将child变为parent,parent变为child->_parent继续往上一层调整
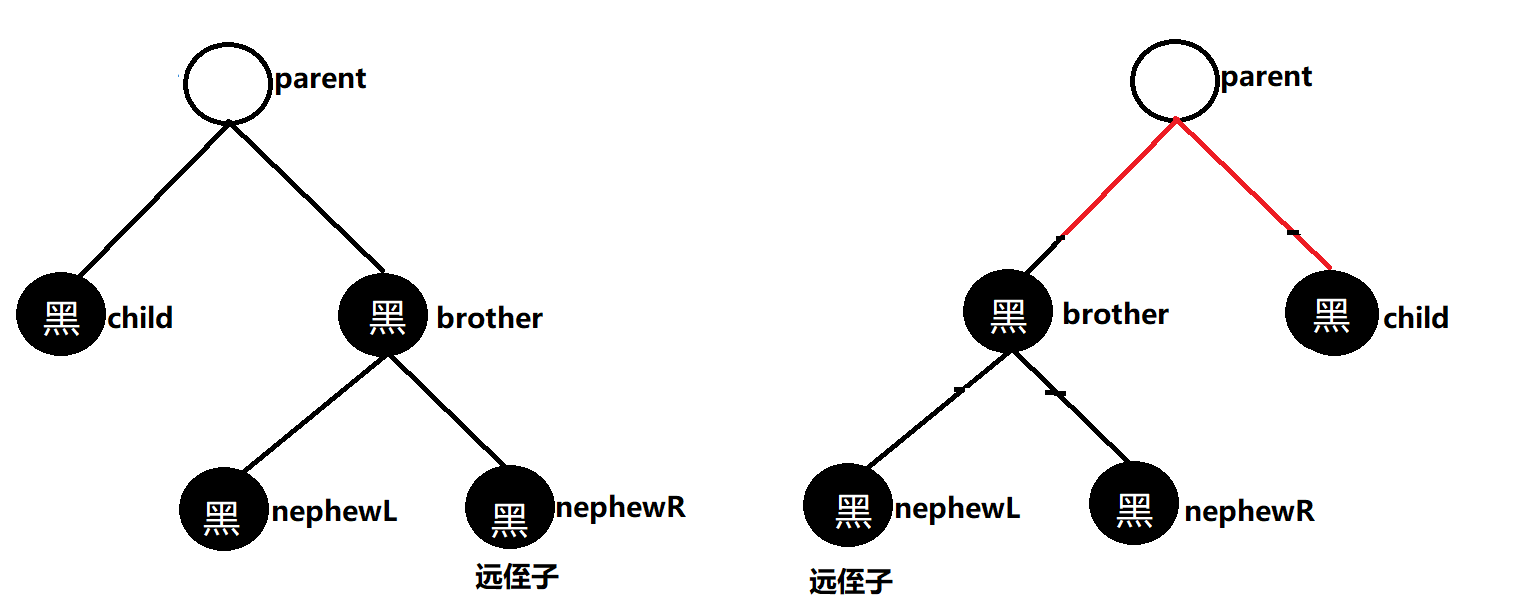
- 要删除的结点只能也只有这样的特征,其他特征都不存在。
删除的代码过长,请在源代码处查询
2.3查找
红黑树(二叉搜索树)的查找就是从根结点开始,沿着某个分支逐层向下比较的过程。先将要查找的值与根结点值比较,如果相等则查找成功;如果不相等,若查找的值小于根结点值,则在根结点的左子树上查找,否则在根结点的右子树上查找;没有找到则返回nullptr。
// 红黑树的查找
Node* Find(const K& key)
{
Node* pos = _root;
while (pos != nullptr)
{
if (pos->_kv.first > key)
{
pos = pos->_left;
}
else if (pos->_kv.first < key)
{
pos = pos->_right;
}
else
{
return pos;
}
}
return nullptr;
}
// [ ]运算符重载
V& operator[](const K& key)
{
return (((this->Insert(make_pair(key, V()))).first)->_kv).second;
}
七.程序演示
1.程序的操作
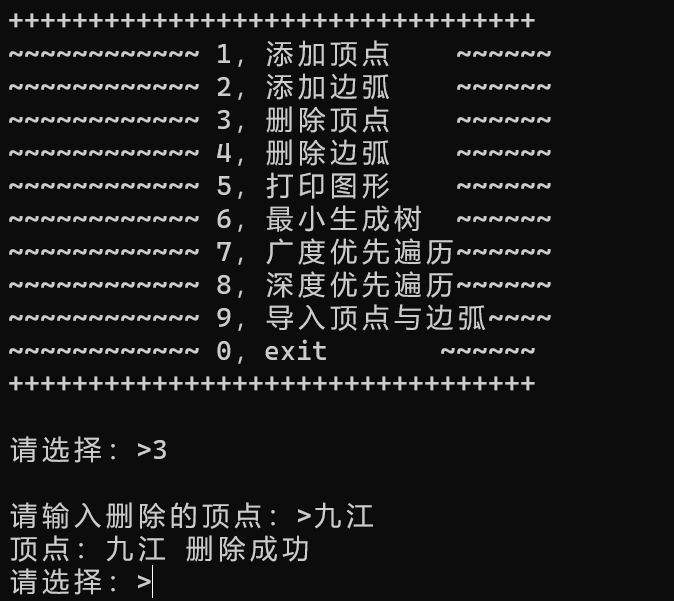
如图所示,程序有以下几个功能。

1.1添加顶点
选择输入1添加顶点,再输入顶点的名称即可。

1.2添加边弧
选择输入2添加边弧,先输入起始顶点,再终止顶点,最后输入边弧的权值即可。

1.3删除顶点
选择输入3删除顶点,再输入顶点的名称即可。
1.4删除边弧
选择输入4删除边弧,先输入起始顶点,再终止顶点即可(如果输入的顶点不存在,则删除失败)。

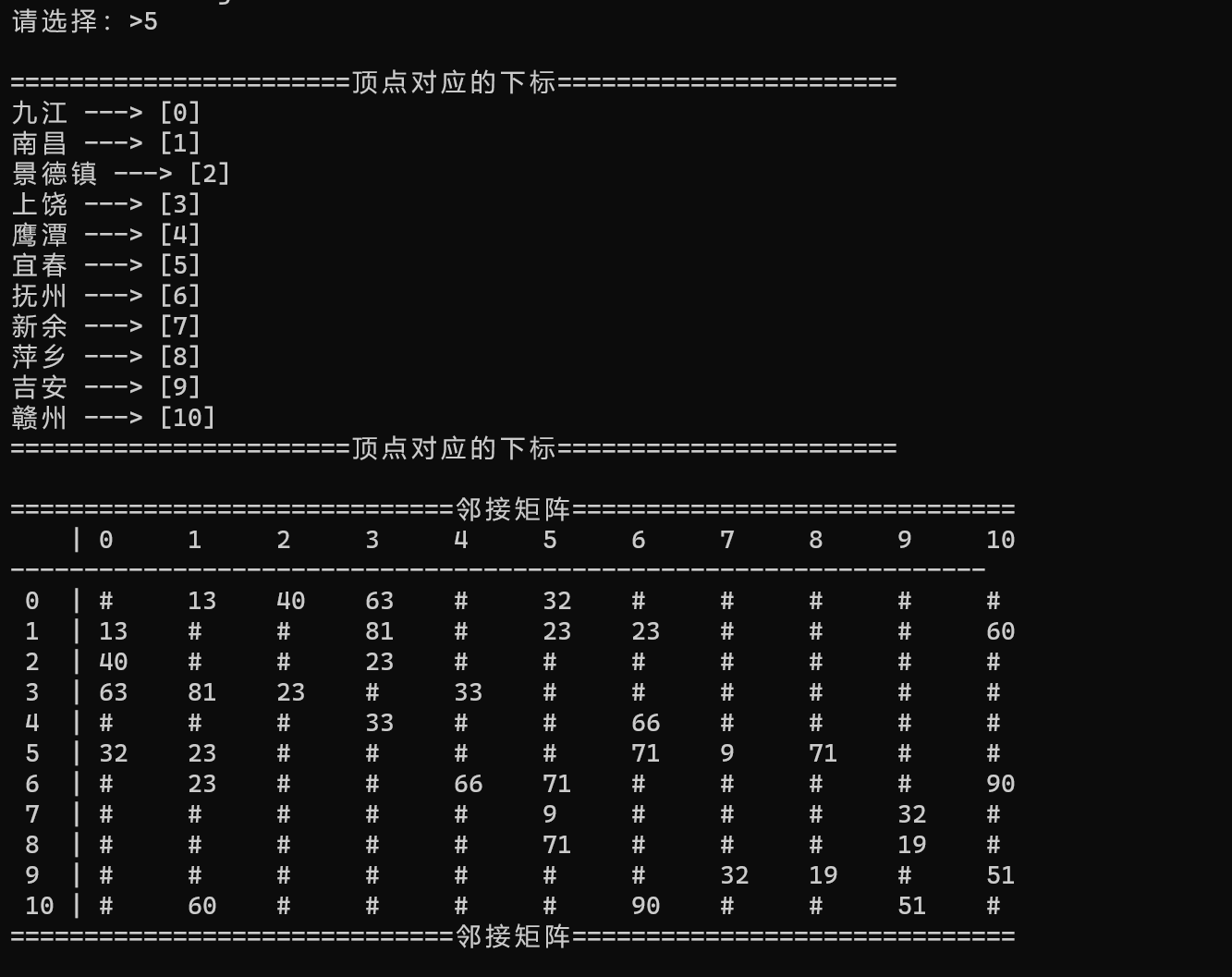
1.5打印图形
选择输入5打印图形,打印的内容有顶点对应的下标以及邻接矩阵。
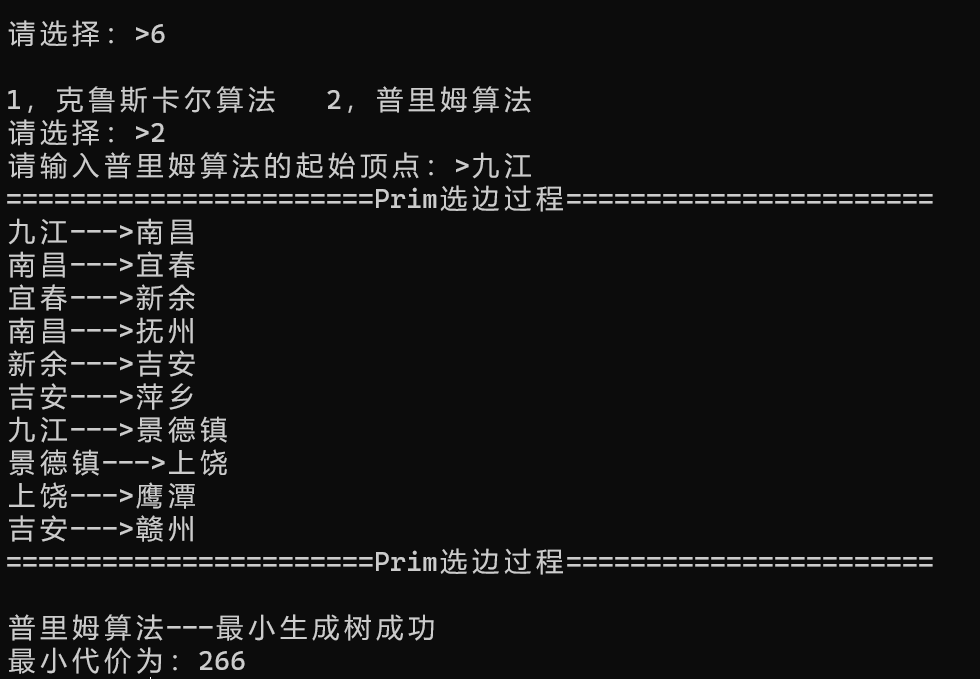
1.6最小生成树
选择输入6进行构造出最小生成树,可以选择:1,克鲁斯卡尔算法 2,普里姆算法(需要再输入一个起始顶点)。

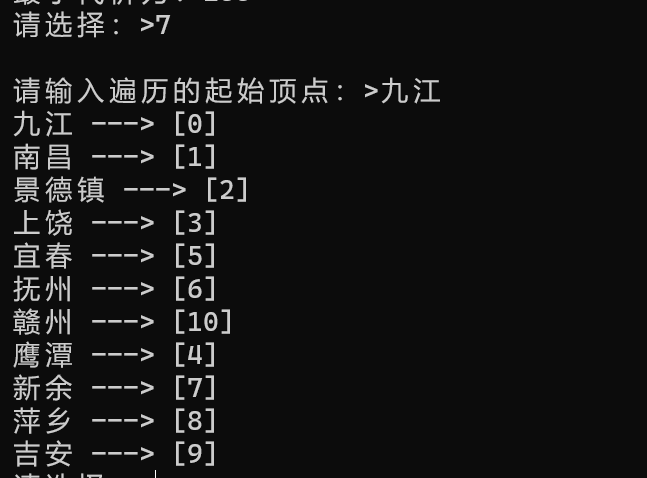
1.7BFS
选择输入7BFS,再输入遍历起始顶点的名称即可。
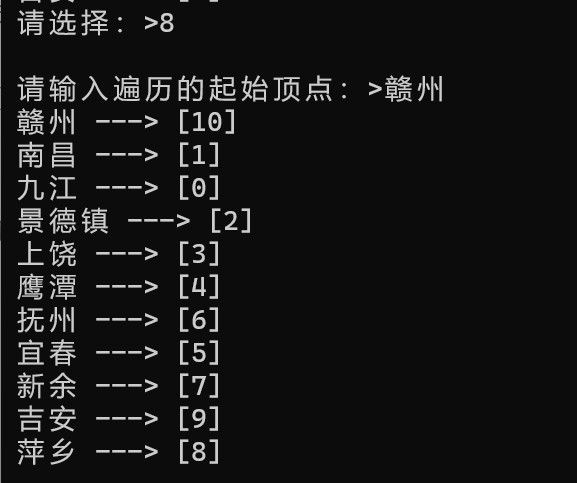
1.8DFS
选择输入8DFS,再输入遍历起始顶点的名称即可。
2.程序的测试
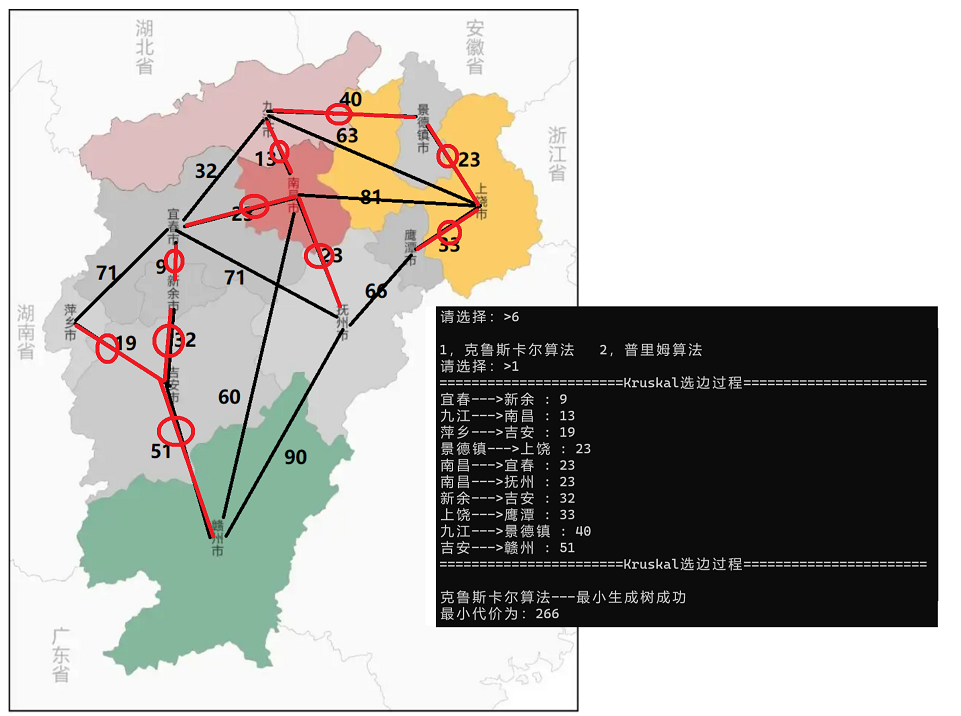
根据下图在程序中输入顶点及顶点与顶点之间的权值。

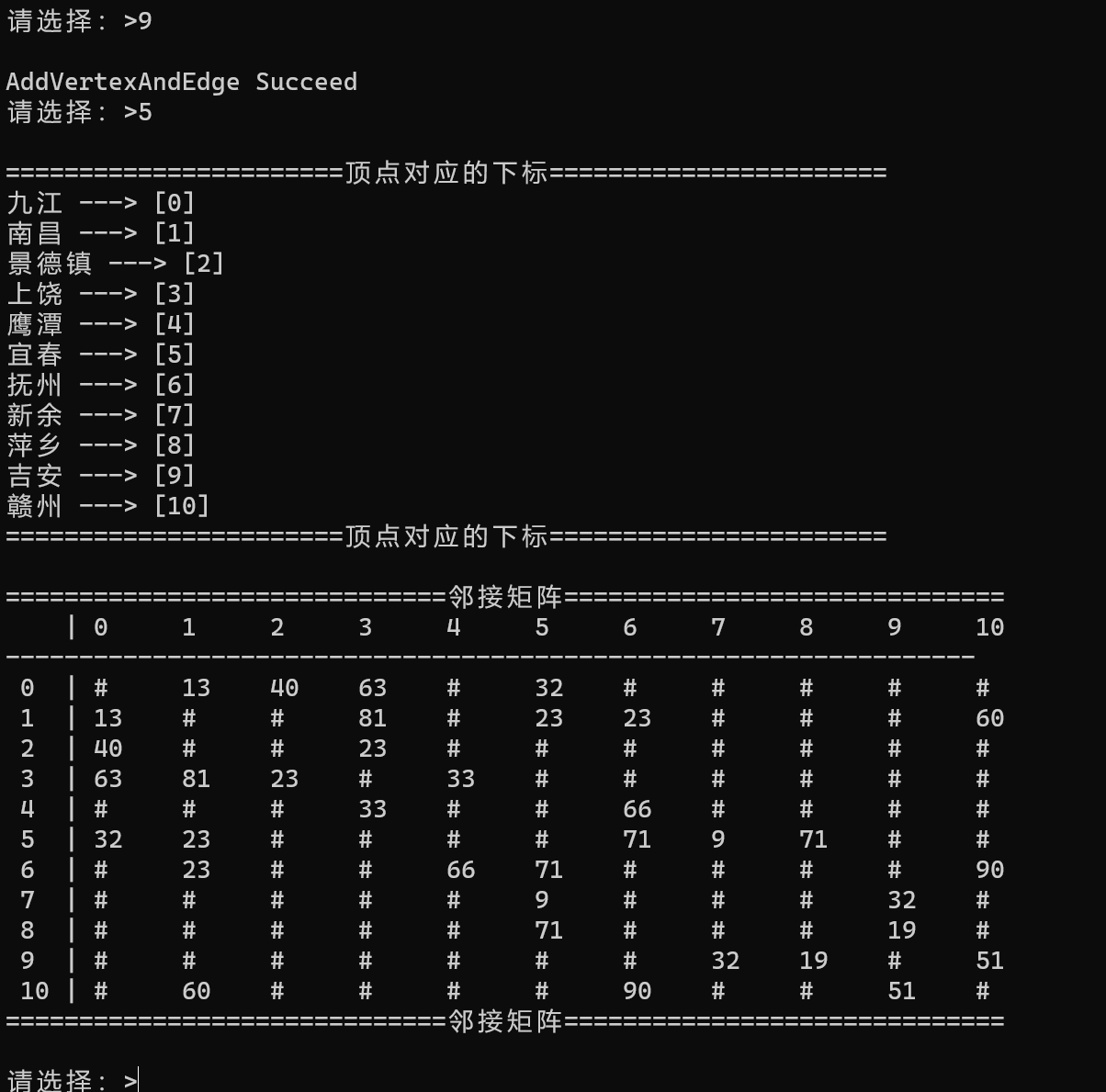
通过Kruskal算法和Prim算法(起始顶点为南昌)得到最小生成树从而解决掉课题问题。
Kruskal:
Prim:
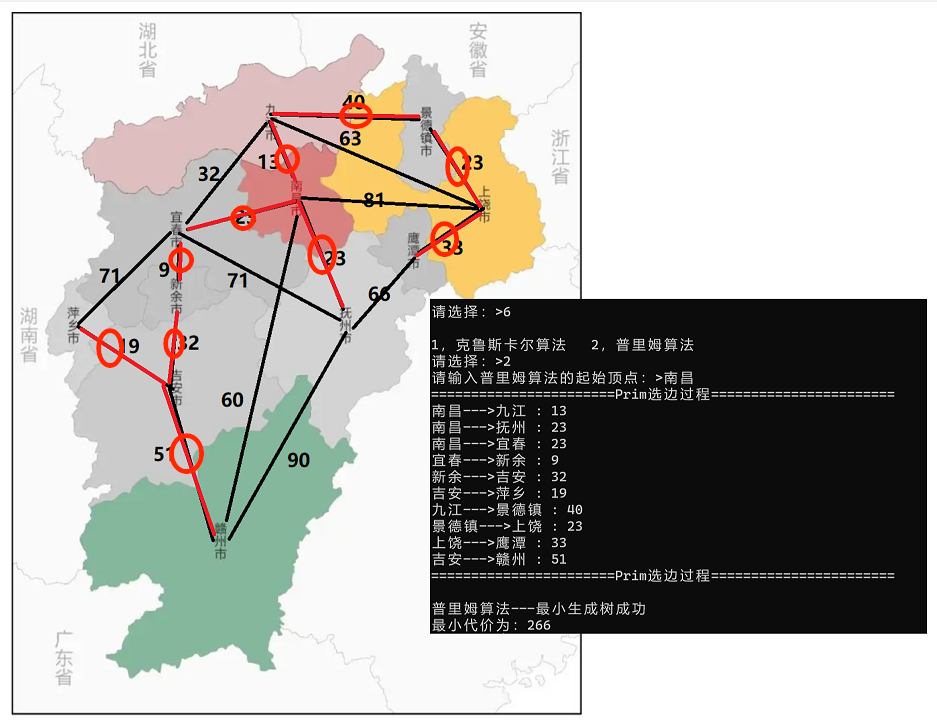
注意:最小生成树并不唯一(也并不是百分百为最优解),但代码是“死”的。所以选择通过Kruskal算法和Prim算法(不同起始顶点)分别产生最小生成树来做比较选择合适的方案。
八.课设总结
遇到的问题:
- 为了实现图的数据结构,纠结使用邻接矩阵还是邻接表作为图的存储结构。最后分析到Kruskal算法和Prim算法都需要频繁访问顶点及边,所以选择使用邻接矩阵作为图的存储结构。
- Kruskal算法在选边的时候如何判断成不成环,经过查看书籍《算法导论》才知道需要用到并查集。
- Prim算法如何区分已选的顶点集合与未选的顶点集合,用位图或者vector**<bool>**。
- 堆的实现,如何通过一份代码既能使用小堆又能使用大堆,通过了解c++STL的容器priority_queue的实现原理,才明白是通过类模板的实例化传对应的仿函数来实现的。
- 如何通过位运算来操作比特位,了解了数据是如何在虚拟内存中存储的。
- 如何实现红黑树修复过程中的旋转,通过三叉链来实现旋转更加简单,但也增加了插入与删除的负担。
- 红黑树的删除规则特别难和杂,只能对着b站视频和候捷老师的《STL源码剖析》一点一点的实现。
心得及体会:
- 只有将学到的理论知识,通过代码实现,自己的代码能力才会有质的提升。
- 基础知识特别重要,只有掌握好基础知识,才能学好更深的知识。
- 在编程时,遇到bug调试特别重要。
程序设计不足:
- 在实现该程序时,没有用到异常,当不按要求输入时,程序可能会崩溃。
- 没有用到文件或者数据库的知识,输入顶点和边需要自己操作比较麻烦。
- 删除顶点或者删除边弧的操作,时间复杂度与空间复杂度过高,效率低下。
九.源代码
[源码地址](数据结构课设/数据结构课设 · yx_零叁/C与C++ - 码云 - 开源中国 (gitee.com))
1.Test.cxx
#define _CRT_SECURE_NO_WARNINGS 1
#include <iostream>
#include <cstdio>
#include <functional>
#include <vector>
#include <string>
#include <queue>
#include <utility>
#include <cassert>
#include <ctime>
#include <Windows.h>
#include "UnionFindSet.hpp"
#include "RedBlackTree.hpp"
#include "BitMap.hpp"
#include "Heap.hpp"
#include "Graph.hpp"
using namespace std;
void Menu()
{
printf("\n+++++++++++++++++++++++++++++++++\n");
printf("~~~~~~~~~~~~ 1,添加顶点 ~~~~~~\n");
printf("~~~~~~~~~~~~ 2,添加边弧 ~~~~~~\n");
printf("~~~~~~~~~~~~ 3,删除顶点 ~~~~~~\n");
printf("~~~~~~~~~~~~ 4,删除边弧 ~~~~~~\n");
printf("~~~~~~~~~~~~ 5,打印图形 ~~~~~~\n");
printf("~~~~~~~~~~~~ 6,最小生成树 ~~~~~~\n");
printf("~~~~~~~~~~~~ 7,广度优先遍历~~~~~~\n");
printf("~~~~~~~~~~~~ 8,深度优先遍历~~~~~~\n");
printf("~~~~~~~~~~~~ 9,导入顶点与边弧~~~~\n");
printf("~~~~~~~~~~~~ 0,exit ~~~~~~\n");
printf("+++++++++++++++++++++++++++++++++\n\n");
}
void AddVertexAndEdge(YX::Graph<std::string>& undirectedGraph)
{
std::vector <std::string > vStr={
{"九江"}, { "南昌" }, { "景德镇" },
{ "上饶" }, { "鹰潭" }, { "宜春" },
{ "抚州" }, { "新余" }, { "萍乡" },
{ "吉安" }, { "赣州" }
};
for (const auto& e : vStr)
{
undirectedGraph.AddVertex(e);
}
undirectedGraph.AddEdge("九江", "南昌",13);
undirectedGraph.AddEdge("九江", "景德镇", 40);
undirectedGraph.AddEdge("九江", "上饶", 63);
undirectedGraph.AddEdge("九江", "宜春", 32);
undirectedGraph.AddEdge("南昌", "上饶", 81);
undirectedGraph.AddEdge("南昌", "抚州", 23);
undirectedGraph.AddEdge("南昌", "宜春", 23);
undirectedGraph.AddEdge("南昌", "赣州", 60);
undirectedGraph.AddEdge("赣州", "吉安", 51);
undirectedGraph.AddEdge("赣州", "抚州", 90);
undirectedGraph.AddEdge("吉安","萍乡",19);
undirectedGraph.AddEdge("吉安", "新余", 32);
undirectedGraph.AddEdge("宜春", "新余", 9);
undirectedGraph.AddEdge("宜春", "萍乡", 71);
undirectedGraph.AddEdge("宜春", "抚州", 71);
undirectedGraph.AddEdge("鹰潭", "抚州", 66);
undirectedGraph.AddEdge("鹰潭", "上饶", 33);
undirectedGraph.AddEdge("上饶", "景德镇", 23);
}
void Test()
{
int num = 0;
int select = 1;
YX::Graph<std::string> undirectedGraph;
typename YX::Graph<std::string>::VertexType src;
typename YX::Graph<std::string>::VertexType dst;
typename YX::Graph<std::string>::WeightType weight;
do {
if (num % 3 == 0)
{
Menu();
}
typename YX::Graph<std::string>::Self minTree;
int MST = 0;
num++;
printf("请选择:>");
scanf("%d", &select);
std::cout << std::endl;
switch (select)
{
case 1:
printf("请输入添加的顶点:>");
std::cin >> src;
if (undirectedGraph.AddVertex(src))
{
std::cout << "顶点:" << src << " 添加成功" << std::endl;
}
else
{
std::cout << "顶点:" << src << " 添加失败" << std::endl;
}
break;
case 2:
printf("请输入起始顶点:>");
std::cin >> src;
printf("请输入终止顶点:>");
std::cin >> dst;
printf("请输入边弧权值:>");
std::cin >> weight;
if (undirectedGraph.AddEdge(src,dst,weight))
{
std::cout << src << " - " << weight << " -> " << dst << "添加成功" << std::endl;
}
else
{
std::cout << src << " - " << " -> " << dst << "添加失败" << std::endl;
}
break;
case 3:
printf("请输入删除的顶点:>");
std::cin >> src;
if (undirectedGraph.DelVertex(src))
{
std::cout << "顶点:" << src << " 删除成功" << std::endl;
}
else
{
std::cout << "顶点:" << src << " 删除失败" << std::endl;
}
break;
case 4:
printf("请输入起始顶点:>");
std::cin >> src;
printf("请输入终止顶点:>");
std::cin >> dst;
if (undirectedGraph.DelEdge(src, dst))
{
std::cout << src << " - " << weight << " -> " << dst << "删除成功" << std::endl;
}
else
{
std::cout << src << " - " << " -> " << dst << "删除失败" << std::endl;
}
break;
case 5:
undirectedGraph.Print();
break;
case 6:
while (true)
{
printf("1,克鲁斯卡尔算法 2,普里姆算法\n");
printf("请选择:>");
scanf("%d", &MST);
if (MST == 1)
{
auto ret = undirectedGraph.Kruskal(minTree);
if (ret.second)
{
printf("克鲁斯卡尔算法---最小生成树成功\n");
std::cout << "最小代价为:" << ret.first << endl;
}
else
{
printf("克鲁斯卡尔算法---最小生成树失败\n");
}
break;
}
else if (MST == 2)
{
while (true)
{
printf("请输入普里姆算法的起始顶点:>");
std::cin >> src;
if (undirectedGraph.FindVertexIndex(src) != -1)
{
break;
}
printf("顶点输入错误,请重新输入!!!\n");
}
auto ret = undirectedGraph.Prim(minTree,src);
if (ret.second)
{
printf("普里姆算法---最小生成树成功\n");
std::cout << "最小代价为:" << ret.first << endl;
}
else
{
printf("普里姆算法---最小生成树失败\n");
}
break;
}
else
{
printf("选择错误,请重新输入!!!\n");
}
}
break;
case 7:
printf("请输入遍历的起始顶点:>");
std::cin >> src;
undirectedGraph.BFS(src);
break;
case 8:
printf("请输入遍历的起始顶点:>");
std::cin >> src;
undirectedGraph.DFS(src);
break;
case 9:
AddVertexAndEdge(undirectedGraph);
printf("AddVertexAndEdge Succeed\n");
break;
default:
printf("选择错误,请重新输入!!!\n");
break;
}
} while (select != 0);
printf("Exit successfully!!!");
}
int main(int, char**, char**)
{
//YX::TestRedBlackTree();
//YX::TestUnionFindSet();
//YX::TestHeap();
//YX::TestGraph();
Test();
return 0;
}
2.Graph.hpp
#pragma once
namespace YX
{
template<class V,class W=int,W W_MAX=INT_MAX,bool Directed=false>
class Graph
{
private:
std::vector<V> _vertexs; // 顶点集合,下标找顶点
std::vector<vector<W>> _matrix; // 邻接矩阵,顶点与顶点之间的权值
YX::RedBlackTree<V, int> _findIndexTree; // 顶点与下标的映射,顶点找下标
public:
typedef Graph<V, W, W_MAX, Directed> Self;
typedef W WeightType;
typedef V VertexType;
Graph() = default;
Graph(const V* arr, int n)
{
_vertexs.reserve(n);
for (int i = 0; i < n; i++)
{
_vertexs.push_back(arr[i]);
_findIndexTree[arr[i]] = i;
}
_matrix.resize(n, std::vector<W>(n, W_MAX));
}
int FindVertexIndex(const V& v) // 找顶点的下标
{
YX::RedBlackTreeNode<V, int>* pos = _findIndexTree.Find(v);
if (pos != nullptr)
{
return pos->_kv.second; // 找到返回对应顶点的下标
}
else
{
//assert(false);
return -1; // 没有找到返回-1
}
}
bool AddEdge(const V& src, const V& dst,const W& w) // 添加边
{
int srci = FindVertexIndex(src);
int dsti = FindVertexIndex(dst);
if (srci == -1 || dsti == -1)
return false;
_matrix[srci][dsti] = w;
if (!Directed) // 如果为无向图,再添加dst到src的边
{
_matrix[dsti][srci] = w;
}
return true;
}
bool DelEdge(const V& src, const V& dst) // 删除边
{
int srci = FindVertexIndex(src);
int dsti = FindVertexIndex(dst);
if (srci == -1 || dsti == -1)
return false;
_matrix[srci][dsti] = W_MAX;
if (!Directed) // 如果为无向图,再添加dst到src的边
{
_matrix[dsti][srci] = W_MAX;
}
return true;
}
bool AddVertex(const V& v) // 添加顶点
{
int vi = FindVertexIndex(v);
if (vi != -1) // 顶点已经存在,无需再添加
return false;
_vertexs.push_back(v);
_findIndexTree.Insert(make_pair(v, (int)_vertexs.size() - 1));
for (size_t i = 0; i < _matrix.size(); i++) // 每一行添加一列
{
_matrix[i].push_back(W_MAX);
}
_matrix.push_back(vector<W>(_matrix.size() + 1, W_MAX)); // 添加一行
return true;
}
bool DelVertex(const V& v)
{
int vi = FindVertexIndex(v);
if (vi == -1) // 顶点不已经存在,无需删除
return false;
// 删除_vertexs中的顶点
auto pos = std::find(_vertexs.begin(), _vertexs.end(), v);
if (pos == _vertexs.end())
{
return false;
}
_vertexs.erase(pos);
//_matrix.erase(&_matrix[vi]);
//for (size_t i = 0; i < _matrix.size(); i++)
//{
// _matrix[i].erase(&_matrix[i][vi]);
//}
// 删除行
auto del = std::find(_matrix.begin()+vi, _matrix.end(), _matrix[vi]);
if (del == _matrix.end())
{
return false;
}
_matrix.erase(del);
// 删除列
for (size_t i = 0; i < _matrix.size(); i++)
{
auto ret = std::find(_matrix[i].begin()+vi, _matrix[i].end(), _matrix[i][vi]);
if (ret == _matrix[i].end())
{
return false;
}
_matrix[i].erase(ret);
}
红黑树的删除---不能这样删除,因为顶点映射的下标乱了
/*if (!_findIndexTree.Erase(v))
{
return false;
}*/
// 需要重新映射
RedBlackTree<V, int> newTree;
for (size_t i = 0; i < this->_vertexs.size(); i++)
{
newTree.Insert(make_pair(_vertexs[i], (int)i));
}
this->_findIndexTree.Swap(newTree);
return true;
}
void Print() // 打印顶点与下标的映射与邻接矩阵
{
if (_vertexs.empty())
return;
cout << "=======================顶点对应的下标=======================" << endl;
for (size_t i = 0; i < _vertexs.size(); i++)
{
std::cout << _vertexs[i] << " ---> [" << i << "]" << endl;
}
cout << "=======================顶点对应的下标=======================" << endl << endl;
cout << "==============================邻接矩阵==============================" << endl;
for (size_t i = 0; i < _matrix.size(); i++)
{
if (i == 0)
{
printf(" %-2c | ", ' ');
printf("%-6d", i);
}
else
{
printf("%-6d", i);
}
}
std::cout << std::endl;
for (size_t i = 0; i < _matrix.size(); i++)
{
printf("------");
}
std::cout << std::endl;
for (size_t i = 0; i < _matrix.size(); i++)
{
printf(" %-2d | ", i);
for (size_t j = 0; j < _matrix[i].size(); j++)
{
if (_matrix[i][j] == W_MAX)
{
printf("%-6c", '#');
}
else
{
printf("%-6d", _matrix[i][j]);
}
}
std::cout << std::endl;
}
cout << "==============================邻接矩阵==============================" << endl << endl;
}
void _BFS(int srci,BitMap& visited)
{
std::queue<int> q;
q.push(srci);
visited.Set(srci); // 记录已经入队
while (!q.empty())
{
int index = q.front();
q.pop();
std::cout << _vertexs[index] << " ---> [" << index << "]" << endl;
for (size_t i = 0; i < _matrix[index].size(); i++)
{
if (_matrix[index][i] != W_MAX && !visited[i])
{
q.push(i);
visited.Set(i);
}
}
}
}
void BFS(const V& src) // 广度优先遍历
{
YX::BitMap visited(_vertexs.size());
this->_BFS(FindVertexIndex(src), visited);
for (size_t i = 0; i < _vertexs.size(); i++)
{
if (!visited[i])
{
this->_BFS(i, visited);
}
}
}
void _DFS(int srci, BitMap& visited)
{
std::cout << _vertexs[srci] << " ---> [" << srci << "]" << endl;
visited.Set(srci);
for (size_t i = 0; i < _matrix[srci].size(); i++)
{
if (_matrix[srci][i] != W_MAX && !visited[i])
{
this->_DFS(i, visited);
}
}
}
void DFS(const V& src) // 深度优先遍历
{
BitMap visited(_vertexs.size());
this->_DFS(FindVertexIndex(src), visited);
for (size_t i = 0; i < _vertexs.size(); i++)
{
if (!visited[i])
{
this->_DFS(i, visited);
}
}
}
struct Edge
{
int _srci;
int _dsti;
W _weight;
Edge() = default;
Edge(const int& srci, const int& dsti, const W& weight)
:_srci(srci)
,_dsti(dsti)
,_weight(weight)
{}
bool operator>(const Edge& e) const
{
return this->_weight > e._weight;
}
bool operator<(const Edge& e) const
{
return this->_weight < e._weight;
}
};
pair<W,bool> Kruskal(Self& minTree)
{
size_t vertexCount = this->_vertexs.size();
minTree._vertexs = this->_vertexs;
minTree._findIndexTree = this->_findIndexTree;
minTree._matrix.resize(vertexCount, vector<W>(vertexCount, W_MAX));
// 将所有的边压入小根堆中
Heap<Edge, std::greater<Edge>> hp;
for (size_t i = 0; i < _matrix.size(); i++)
{
for (size_t j = 0; j < _matrix[i].size(); j++)
{
if (i < j && _matrix[i][j] != W_MAX)
{
hp.Push(Edge(i, j, _matrix[i][j]));
}
}
}
// 创建n棵树的并查集
UnionFindSet ufs(vertexCount);
W retW=W();
size_t minVertexCount = 0;
cout << "=======================Kruskal选边过程=======================" << endl;
while (!hp.Empty())
{
// 取出权值最小的边
Edge minEdge = hp.Top();
hp.Pop();
// 如果这两个顶点不在一个集合,则将这条边添加到minTree
if (!ufs.IsInSet(minEdge._srci, minEdge._dsti))
{
cout << minTree._vertexs[minEdge._srci] << "--->" << minTree._vertexs[minEdge._dsti] << " : " << minEdge._weight << std::endl;
Sleep(1000);
minTree.AddEdge(minTree._vertexs[minEdge._srci], minTree._vertexs[minEdge._dsti], minEdge._weight);
// 再将这两个顶点合并成一个集合
ufs.Union(minEdge._srci, minEdge._dsti);
retW += minEdge._weight;
minVertexCount++;
}
if (minVertexCount == vertexCount - 1)
{
break;
}
}
cout << "=======================Kruskal选边过程=======================" << endl << endl;
if (minVertexCount == vertexCount - 1)
{
return make_pair(retW, true);
}
else
{
return make_pair(W(), false);
}
}
pair<W, bool> Prim(Self& minTree, const V& src)
{
int srci = FindVertexIndex(src);
if (srci == -1)
return make_pair(W(), false);
size_t vertexCount = this->_vertexs.size();
minTree._vertexs = this->_vertexs;
minTree._findIndexTree = this->_findIndexTree;
minTree._matrix.resize(vertexCount, vector<W>(vertexCount, W_MAX));
Heap<Edge, std::greater<Edge>> hp;
// 用位图标记已选的顶点X集合和未选的顶点Y集合 X:1 Y:0
BitMap XY(vertexCount);
XY.Set(srci);
for (size_t i = 0; i < _matrix[srci].size(); i++)
{
// 将与src相连的顶点对应的边入堆
if (_matrix[srci][i] != W_MAX && XY[srci] && !XY[i])
{
hp.Push(Edge(srci, i, _matrix[srci][i]));
}
}
W retW = W();
size_t minVertexCount = 0;
cout << "=======================Prim选边过程=======================" << endl;
while (!hp.Empty())
{
Edge minEdge = hp.Top();
hp.Pop();
if (XY[minEdge._srci] && !XY[minEdge._dsti])
{
cout << minTree._vertexs[minEdge._srci] << "--->" << minTree._vertexs[minEdge._dsti] <<" : "<< minEdge._weight<< std::endl;
Sleep(1000);
// 只有srci在X集合,dsti在Y集合,才能加入到minTree
minTree.AddEdge(minTree._vertexs[minEdge._srci], minTree._vertexs[minEdge._dsti], minEdge._weight);
XY.Set(minEdge._dsti);
for (size_t i = 0; i < _matrix[minEdge._dsti].size(); i++)
{
// 将与dsti相连的顶点对应的边入堆
if (_matrix[minEdge._dsti][i] != W_MAX && XY[minEdge._dsti] && !XY[i])
{
hp.Push(Edge(minEdge._dsti, i, _matrix[minEdge._dsti][i]));
}
}
retW += minEdge._weight;
minVertexCount++;
}
if (minVertexCount == vertexCount - 1)
{
break;
}
}
cout << "=======================Prim选边过程=======================" << endl << endl;
if (minVertexCount == vertexCount - 1)
{
return make_pair(retW, true);
}
else
{
return make_pair(W(), false);
}
}
void InOrder()
{
this->_findIndexTree.InOrder();
}
};
void TestGraph()
{
const char* str = "abcdefghi";
Graph<char> g(str, strlen(str));
g.AddEdge('a', 'b', 4);
g.AddEdge('a', 'h', 8);
g.AddEdge('b', 'c', 8);
g.AddEdge('b', 'h', 11);
g.AddEdge('c', 'd', 7);
g.AddEdge('c', 'i', 2);
g.AddEdge('c', 'f', 4);
g.AddEdge('d', 'e', 9);
g.AddEdge('d', 'f', 14);
g.AddEdge('e', 'f', 10);
g.AddEdge('f', 'g', 2);
g.AddEdge('g', 'h', 1);
g.AddEdge('g', 'i', 6);
g.AddEdge('h', 'i', 7);
g.Print();
g.InOrder();
g.DelVertex('a');
g.InOrder();
g.AddVertex('a');
g.InOrder();
g.Print();
/*Graph<char>::Self minTree;
auto ret = g.Prim(minTree, 'a');
std::cout << "Prim:" << ret.first << std::endl;*/
/*auto ret = g.Kruskal(minTree);
std::cout << "Kruskal:" << ret.first << std::endl;*/
}
}
3.Heap.hpp
#pragma once
namespace YX
{
// 默认大堆
template<typename T,typename Compare=std::less<T>,typename Container=std::vector<T>>
class Heap
{
private:
Container _con;
Compare _com;
// 向上调整
void AdjustUp(int child)
{
int parent = (child - 1) / 2;
while (child > 0)
{
//if (this->_con[child] > this->_con[parent])
if (this->_com(this->_con[parent], this->_con[child]))
{
std::swap(this->_con[child], this->_con[parent]);
child = parent;
parent = (child - 1) / 2;
}
else
{
break;
}
}
}
// 向下调整
void AdjustDown(int parent)
{
int child = 2 * parent + 1;
while (child < (int)this->_con.size())
{
//if (child + 1 < this->_con.size() && this->_con[child + 1] > this->_con[child])
if (child + 1 < (int)this->_con.size() && this->_com(this->_con[child], this->_con[child+1]))
{
child++;
}
//if (this->_con[child] > this->_con[parent])
if (this->_com(this->_con[parent], this->_con[child]))
{
std::swap(this->_con[child], this->_con[parent]);
parent = child;
child = 2 * parent + 1;
}
else
{
break;
}
}
}
public:
bool Empty()
{
return this->_con.empty();
}
const T& Top()
{
if (this->_con.empty())
{
perror("Heap::Top");
exit(1);
}
return this->_con[0];
}
void Push(const T& val)
{
// 入堆,插入到vector最后,然后从最后一个元素开始进行向上调整
this->_con.push_back(val);
this->AdjustUp(this->_con.size() - 1);
}
void Pop()
{
if (this->_con.empty())
{
perror("Heap::Pop");
return;
}
// 出堆,堆顶元素与最后一个元素交换,再从堆顶开始进行向下调整
std::swap(this->_con[0], this->_con[this->_con.size() - 1]);
this->_con.pop_back();
this->AdjustDown(0);
}
std::size_t Size()
{
return this->_con.size();
}
void Print()
{
for (const auto& e : this->_con)
{
std::cout << e << " ";
}
std::cout << std::endl;
}
};
void TestHeap()
{
int arr[] = { 1,2,3,4,5,6,7,8,9,0 };
Heap<int> hp;
for (auto e : arr)
{
hp.Push(e);
}
hp.Print();
hp.Pop();
hp.Print();
}
}
4.BitMap.hpp
#pragma once
namespace YX
{
// 位图
class BitMap
{
private:
std::vector<char> _bitMap;
public:
BitMap(size_t N)
:_bitMap(N/sizeof(char)+1,0)
{}
void Set(size_t index) // 改为真
{
size_t group = index / 8;
size_t groupIndex = index % 8;
this->_bitMap[group] |= (1 << groupIndex);
}
void ReSet(size_t index) // 改为假
{
size_t group = index / 8;
size_t groupIndex = index % 8;
this->_bitMap[group] &= (~(1 << groupIndex));
}
bool Test(size_t index) // 判断对应下标真假
{
size_t group = index / 8;
size_t groupIndex = index % 8;
size_t ret = (this->_bitMap[group] & (1 << groupIndex));
return !(ret == 0);
}
bool operator[](size_t index)
{
return this->Test(index);
}
};
}
5.UnionFindSet.hpp
#pragma once
namespace YX
{
//template<class T>
//class UnionFindSet
//{
//private:
// std::vector<int> _ufs; // 双亲表示法
// std::vector<T> _valArr; // 下标映射值
// std::map<T, int> _indexMap; // 值映射下标
//};
class UnionFindSet
{
private:
std::vector<int> _ufs;
public:
UnionFindSet(size_t n)
:_ufs(n,-1)
{}
bool Union(int x1, int x2) // 两个集合合并
{
int root1 = FindRootIndex(x1);
int root2 = FindRootIndex(x2);
if (root1 == root2) // 已经在一个集合,不需要合并
return false;
// x2合并到x1中
this->_ufs[root1] += this->_ufs[root2];
this->_ufs[root2] = root1;
return true;
}
int FindRootIndex(int x) // 找根结点的下标
{
int root = x;
while (this->_ufs[root] >= 0)
{
root = this->_ufs[root];
}
return root;
}
bool IsInSet(int x1, int x2) // 判断在不在一个集合
{
int root1 = FindRootIndex(x1);
int root2 = FindRootIndex(x2);
return root1 == root2;
}
std::size_t SetCount() // 集合的个数
{
std::size_t count = 0;
for (auto& e : this->_ufs)
{
if (e < 0)
count++;
}
return count;
}
};
void TestUnionFindSet()
{
UnionFindSet ufs(10);
ufs.Union(1, 2);
ufs.Union(1, 3);
ufs.Union(6, 9);
std::cout << ufs.FindRootIndex(3) << std::endl;
std::cout << ufs.IsInSet(3,9) << std::endl;
std::cout << ufs.SetCount() << std::endl;
}
}
6.RedBlackTree.hpp
#pragma once
using namespace std;
namespace YX
{
// 枚举类型,标识结点的颜色
enum class Colour
{
RED,
BLACK,
};
template<typename K, typename V>
struct RedBlackTreeNode
{
// 三叉链
struct RedBlackTreeNode<K, V>* _left;
struct RedBlackTreeNode<K, V>* _right;
struct RedBlackTreeNode<K, V>* _parent;
// 结点颜色
Colour _colour;
// Key-Value 索引
pair<K, V> _kv;
RedBlackTreeNode(const pair<K, V>& kv)
:_left(nullptr)
, _right(nullptr)
, _parent(nullptr)
, _colour(Colour::RED)
, _kv(kv)
{}
};
/*
1,根结点是黑色
2,除根结点外,其他结点不是黑色就是红色
3,红色结点的双亲或者孩子不能再是红色
4,每条路径上的黑色结点数目相同
5,NIL结点是黑色
6,最长路径不超过最短路径的两倍
*/
template<class K, class V>
class RedBlackTree
{
typedef RedBlackTreeNode<K, V> Node;
private:
Node* _root = nullptr;
// 右单旋
void _RightRotate(Node* parent)
{
Node* parentParent = parent->_parent;
Node* subLeft = parent->_left;
Node* subLeftRight = subLeft->_right;
subLeft->_right = parent;
parent->_parent = subLeft;
parent->_left = subLeftRight;
if (subLeftRight != nullptr)
{
subLeftRight->_parent = parent;
}
// parent为根结点特殊处理
if (parent == _root)
{
_root = subLeft;
subLeft->_parent = nullptr;
}
else
{
if (parentParent->_left == parent)
{
parentParent->_left = subLeft;
}
else if (parentParent->_right == parent)
{
parentParent->_right = subLeft;
}
subLeft->_parent = parentParent;
}
}
// 左单旋
void _LeftRotate(Node* parent)
{
Node* parentParent = parent->_parent;
Node* subRight = parent->_right;
Node* subRightLeft = subRight->_left;
subRight->_left = parent;
parent->_parent = subRight;
parent->_right = subRightLeft;
if (subRightLeft != nullptr)
{
subRightLeft->_parent = parent;
}
// parent为根结点特殊处理
if (parent == _root)
{
_root = subRight;
subRight->_parent = nullptr;
}
else
{
if (parentParent->_left == parent)
{
parentParent->_left = subRight;
}
else if (parentParent->_right == parent)
{
parentParent->_right = subRight;
}
subRight->_parent = parentParent;
}
}
// prev:插入结点的双亲,curr:插入结点
void _RepairInsert(Node* prev, Node* curr)
{
// 因为插入的结点颜色是红色,所以只有当双亲存在且双亲颜色为红才需要修复
while (prev != nullptr && prev->_colour == Colour::RED)
{
// 双亲存在且为红,则祖父一定存在
Node* grandfather = prev->_parent;
if (grandfather->_left == prev)
{
Node* uncle = grandfather->_right;
// 叔叔存在且为红,变色即可
if (uncle != nullptr && uncle->_colour == Colour::RED)
{
prev->_colour = uncle->_colour = Colour::BLACK;
grandfather->_colour = Colour::RED;
}
else // 叔叔不存在或者叔叔存在且为黑,变色加旋转处理
{
if (prev->_left == curr) // 左左---右旋
{
_RightRotate(grandfather);
prev->_colour = Colour::BLACK;
grandfather->_colour = Colour::RED;
}
else if (prev->_right == curr) // 左右---左右双旋
{
_LeftRotate(prev);
_RightRotate(grandfather);
curr->_colour = Colour::BLACK;
grandfather->_colour = Colour::RED;
}
break;
}
}
else if (grandfather->_right == prev)
{
Node* uncle = grandfather->_left;
// 叔叔存在且为红,只需要变色即可
if (uncle != nullptr && uncle->_colour == Colour::RED)
{
prev->_colour = uncle->_colour = Colour::BLACK;
grandfather->_colour = Colour::RED;
}
else // 叔叔不存在或者叔叔存在为黑色,变色加旋转处理
{
if (prev->_right == curr) // 右右---左旋
{
_LeftRotate(grandfather);
grandfather->_colour = Colour::RED;
prev->_colour = Colour::BLACK;
}
else if (prev->_left == curr) // 右左---右左旋
{
_RightRotate(prev);
_LeftRotate(grandfather);
grandfather->_colour = Colour::RED;
curr->_colour = Colour::BLACK;
}
break;
}
}
curr = grandfather;
prev = curr->_parent;
}
}
// prev:删除结点的双亲,curr:删除结点
void _RepairErase(Node* prev, Node* curr)
{
// 删除结点为红色可以直接删除
if (curr->_colour == Colour::RED)
{
return;
}
// 删除结点为黑色并且有一个孩子结点(该孩子结点一定是红色),将该孩子结点变黑即可
if (curr->_colour == Colour::BLACK)
{
if (curr->_left != nullptr && curr->_left->_colour == Colour::RED)
{
curr->_left->_colour = Colour::BLACK;
return;
}
else if (curr->_right != nullptr && curr->_right->_colour == Colour::RED)
{
curr->_right->_colour = Colour::BLACK;
return;
}
}
// 删除结点是黑色并且没有孩子
while (curr != _root)
{
if (prev->_left == curr)
{
Node* brother = prev->_right;
Node* leftNephew = brother->_left;
Node* rightNephew = brother->_right;
if (brother->_colour == Colour::BLACK)
{
// 兄弟结点为黑色,远侄子为红色 --- 变色加旋转
if (rightNephew != nullptr && rightNephew->_colour == Colour::RED)
{
// 双亲与兄弟交换颜色
std::swap(brother->_colour, prev->_colour);
rightNephew->_colour = Colour::BLACK;
_LeftRotate(prev);
return;
} // 兄弟结点为黑色,近侄子为红色---变色加旋转
else if (leftNephew != nullptr && leftNephew->_colour == Colour::RED)
/*else if (leftNephew != nullptr && leftNephew->_colour == Colour::RED
&& rightNephew != nullptr && rightNephew->_colour == Colour::BLACK)*/
{
std::swap(brother->_colour, leftNephew->_colour);
_RightRotate(brother);
} // 兄弟结点为黑色,两个侄子都为黑色---变色
else if ((rightNephew == nullptr || rightNephew->_colour == Colour::BLACK)
&& (leftNephew == nullptr || leftNephew->_colour == Colour::BLACK))
{
brother->_colour = Colour::RED;
if (prev == _root || prev->_colour == Colour::RED)
{
prev->_colour = Colour::BLACK;
return;
}
curr = prev;
prev = curr->_parent;
}
} // 兄弟结点为红色---变色加旋转
else if (brother->_colour == Colour::RED)
{
std::swap(prev->_colour, brother->_colour);
_LeftRotate(prev);
}
}
else if (prev->_right == curr)
{
Node* brother = prev->_left;
Node* leftNephew = brother->_left;
Node* rightNephew = brother->_right;
if (brother->_colour == Colour::BLACK)
{
// 兄弟结点为黑色,远侄子为红色 --- 变色加旋转
if (leftNephew != nullptr && leftNephew->_colour == Colour::RED)
{
std::swap(prev->_colour, brother->_colour);
leftNephew->_colour = Colour::BLACK;
_RightRotate(prev);
return;
} // 兄弟结点为黑色,近侄子为红色---变色加旋转
else if (rightNephew != nullptr && rightNephew->_colour == Colour::RED
&& leftNephew != nullptr && leftNephew->_colour == Colour::BLACK)
{
std::swap(brother->_colour, rightNephew->_colour);
_LeftRotate(brother);
} // 兄弟结点为黑色,两个侄子都为黑色---变色
else if ((rightNephew == nullptr || rightNephew->_colour == Colour::BLACK)
&& (leftNephew == nullptr || leftNephew->_colour == Colour::BLACK))
{
brother->_colour = Colour::RED;
if (prev == _root || prev->_colour == Colour::RED)
{
prev->_colour = Colour::BLACK;
return;
}
curr = prev;
prev = curr->_parent;
}
}
else if (brother->_colour == Colour::RED)
{
std::swap(prev->_colour, brother->_colour);
_RightRotate(prev);
}
}
}
}
void _Destory(Node* root)
{
if (root == nullptr)
return;
_Destory(root->_left);
_Destory(root->_right);
delete root;
}
Node* _Copy(Node* root, Node* parent)
{
if (root == nullptr)
return nullptr;
Node* newNode = new Node(root->_kv);
newNode->_parent = parent;
newNode->_colour = root->_colour;
newNode->_left = _Copy(root->_left, newNode);
newNode->_right = _Copy(root->_right, newNode);
return newNode;
}
void _InOrder(Node* root)
{
if (root == nullptr)
{
return;
}
_InOrder(root->_left);
cout << root->_kv.first << " : " << root->_kv.second << endl;
_InOrder(root->_right);
}
bool _IsBalance(Node* root, int blackNum, const int& blackReferenceValue)
{
if (root == nullptr)
{
if (blackNum != blackReferenceValue)
{
return false;
}
else
{
return true;
}
}
if (root->_colour == Colour::BLACK)
{
blackNum++;
}
else
{
if (root->_parent->_colour == Colour::RED)
{
return false;
}
}
return _IsBalance(root->_left, blackNum, blackReferenceValue)
&& _IsBalance(root->_right, blackNum, blackReferenceValue);
}
public:
RedBlackTree() = default;
// 红黑树的插入
pair<Node*, bool> Insert(const pair<K, V>& kv)
{
if (_root == nullptr)
{
_root = new Node(kv);
_root->_parent = nullptr;
_root->_colour = Colour::BLACK;
return make_pair(_root, true);
}
Node* prev = nullptr;
Node* curr = _root;
while (curr != nullptr)
{
if (curr->_kv.first > kv.first) // 小往左走
{
prev = curr;
curr = curr->_left;
}
else if (curr->_kv.first < kv.first) // 大往右走
{
prev = curr;
curr = curr->_right;
}
else // 不允许键值冗余
{
return make_pair(curr, false);
}
}
curr = new Node(kv);
if (prev->_kv.first < kv.first)
{
prev->_right = curr;
}
else if (prev->_kv.first > kv.first)
{
prev->_left = curr;
}
curr->_parent = prev;
_RepairInsert(prev, curr);
_root->_colour = Colour::BLACK;
return make_pair(curr, true);
}
// 红黑树的删除
bool Erase(const K& key)
{
if (_root == nullptr)
return false;
Node* prev = nullptr;
Node* curr = _root;
while (curr != nullptr)
{
if (curr->_kv.first < key)
{
prev = curr;
curr = curr->_right;
}
else if (curr->_kv.first > key)
{
prev = curr;
curr = curr->_left;
}
else // 找到了开始删除
{
if (curr->_left == nullptr) // 删除结点有一个孩子结点或者没有
{
if (curr == _root)
{
_root = curr->_right;
}
else
{
_RepairErase(prev, curr);
if (prev->_left == curr)
{
prev->_left = curr->_right;
}
else if (prev->_right == curr)
{
prev->_right = curr->_right;
}
}
if (curr->_right != nullptr)
{
curr->_right->_parent = prev;
}
delete curr;
}
else if (curr->_right == nullptr) // 删除结点有一个孩子结点或者没有
{
if (curr == _root)
{
_root = curr->_left;
}
else
{
_RepairErase(prev, curr);
if (prev->_left == curr)
{
prev->_left = curr->_left;
}
else if (prev->_right == curr)
{
prev->_right = curr->_left;
}
}
if (curr->_left != nullptr)
{
curr->_left->_parent = prev;
}
delete curr;
}
else // 删除结点有两个孩子结点,用替换法删除
{
// 1,找左子树的最大结点
// 2,找右子树的最小结点
Node* leftSubMax = curr->_left;
while (leftSubMax->_right != nullptr)
{
leftSubMax = leftSubMax->_right;
}
pair<K, V> tmpKV = leftSubMax->_kv;
this->Erase(tmpKV.first);
std::swap(curr->_kv, tmpKV);
}
if (_root != nullptr)
{
_root->_colour = Colour::BLACK;
}
return true;
}
}
return false;
}
// 红黑树的查找
Node* Find(const K& key)
{
Node* pos = _root;
while (pos != nullptr)
{
if (pos->_kv.first > key)
{
pos = pos->_left;
}
else if (pos->_kv.first < key)
{
pos = pos->_right;
}
else
{
return pos;
}
}
return nullptr;
}
V& operator[](const K& key)
{
return (((this->Insert(make_pair(key, V()))).first)->_kv).second;
}
// 判断是不是一棵红黑树
bool IsBalance()
{
if (_root == nullptr)
return true;
if (_root->_colour == Colour::RED)
return false;
// 求某条路径上的黑色结点数量
int blackReferenceValue = 0;
Node* curr = _root;
while (curr != nullptr)
{
if (curr->_colour == Colour::BLACK)
blackReferenceValue++;
curr = curr->_left;
}
return _IsBalance(_root, 0, blackReferenceValue);
}
void InOrder()
{
_InOrder(_root);
cout << endl;
}
RedBlackTree(const RedBlackTree<K, V>& tree)
:_root(nullptr)
{
_root = _Copy(tree._root, nullptr);
}
RedBlackTree<K, V>& operator=(RedBlackTree<K, V> tree)
{
std::swap(_root, tree._root);
return *this;
}
~RedBlackTree()
{
_Destory(_root);
_root = nullptr;
}
void Swap(RedBlackTree<K, V>& tree)
{
std::swap(this->_root, tree._root);
}
// 移动构造
RedBlackTree(RedBlackTree<K, V>&& tree) noexcept
:_root(nullptr)
{
this->Swap(tree);
//std::swap(this->_root, tree._root);
}
// 移动赋值
RedBlackTree<K, V>& operator=(RedBlackTree<K, V>&& tree) noexcept
{
std::swap(this->_root, tree._root);
return *this;
}
};
RedBlackTree<int, int> Test()
{
RedBlackTree<int, int> tree;
tree.Insert(make_pair(1,1));
return tree;
}
void TestRedBlackTree()
{
YX::RedBlackTree<int, int> tree=Test();
int arr[] = { 25,33,7,111,234,67865,8768,2323,43434,57687,9,8,7,65,4,32 };
for (auto e : arr)
{
tree.Insert(make_pair(e, e));
cout << "IsBalance:" << tree.IsBalance() << endl;
}
tree.InOrder();
auto pos=tree.Find(1);
if (pos != nullptr)
{
std::cout << pos->_kv.first << ":" << pos->_kv.second << std::endl;
}
/*for (auto e : arr)
{
tree.Erase(e);
cout << "IsBalance:" << tree.IsBalance() << endl;
}
tree.InOrder();*/
}
}
prev->_right = curr->_left;
}
}
if (curr->_left != nullptr)
{
curr->_left->_parent = prev;
}
delete curr;
}
else // 删除结点有两个孩子结点,用替换法删除
{
// 1,找左子树的最大结点
// 2,找右子树的最小结点
Node* leftSubMax = curr->_left;
while (leftSubMax->_right != nullptr)
{
leftSubMax = leftSubMax->_right;
}
pair<K, V> tmpKV = leftSubMax->_kv;
this->Erase(tmpKV.first);
std::swap(curr->_kv, tmpKV);
}
if (_root != nullptr)
{
_root->_colour = Colour::BLACK;
}
return true;
}
}
return false;
}
// 红黑树的查找
Node* Find(const K& key)
{
Node* pos = _root;
while (pos != nullptr)
{
if (pos->_kv.first > key)
{
pos = pos->_left;
}
else if (pos->_kv.first < key)
{
pos = pos->_right;
}
else
{
return pos;
}
}
return nullptr;
}
V& operator[](const K& key)
{
return (((this->Insert(make_pair(key, V()))).first)->_kv).second;
}
// 判断是不是一棵红黑树
bool IsBalance()
{
if (_root == nullptr)
return true;
if (_root->_colour == Colour::RED)
return false;
// 求某条路径上的黑色结点数量
int blackReferenceValue = 0;
Node* curr = _root;
while (curr != nullptr)
{
if (curr->_colour == Colour::BLACK)
blackReferenceValue++;
curr = curr->_left;
}
return _IsBalance(_root, 0, blackReferenceValue);
}
void InOrder()
{
_InOrder(_root);
cout << endl;
}
RedBlackTree(const RedBlackTree<K, V>& tree)
:_root(nullptr)
{
_root = _Copy(tree._root, nullptr);
}
RedBlackTree<K, V>& operator=(RedBlackTree<K, V> tree)
{
std::swap(_root, tree._root);
return *this;
}
~RedBlackTree()
{
_Destory(_root);
_root = nullptr;
}
void Swap(RedBlackTree<K, V>& tree)
{
std::swap(this->_root, tree._root);
}
// 移动构造
RedBlackTree(RedBlackTree<K, V>&& tree) noexcept
:_root(nullptr)
{
this->Swap(tree);
//std::swap(this->_root, tree._root);
}
// 移动赋值
RedBlackTree<K, V>& operator=(RedBlackTree<K, V>&& tree) noexcept
{
std::swap(this->_root, tree._root);
return *this;
}
};
RedBlackTree<int, int> Test()
{
RedBlackTree<int, int> tree;
tree.Insert(make_pair(1,1));
return tree;
}
void TestRedBlackTree()
{
YX::RedBlackTree<int, int> tree=Test();
int arr[] = { 25,33,7,111,234,67865,8768,2323,43434,57687,9,8,7,65,4,32 };
for (auto e : arr)
{
tree.Insert(make_pair(e, e));
cout << "IsBalance:" << tree.IsBalance() << endl;
}
tree.InOrder();
auto pos=tree.Find(1);
if (pos != nullptr)
{
std::cout << pos->_kv.first << ":" << pos->_kv.second << std::endl;
}
/*for (auto e : arr)
{
tree.Erase(e);
cout << "IsBalance:" << tree.IsBalance() << endl;
}
tree.InOrder();*/
}
}
该图来自《算法导论》 ↩︎
该图来自《算法导论》 ↩︎
![【PWN · ret2libc】[CISCN 2019东北]PWN2](https://img-blog.csdnimg.cn/17c7062a14264c4097ff9cc4a747dec7.png)