文章目录
- 10 EM(期望最大)算法
- 10.1 背景介绍
- 10.2 EM算法公式
- 10.2.1 EM算法公式收敛性证明
- 10.2.2 EM算法公式导出
- 10.3 广义EM算法
- 10.3.1 EM有什么作用?
- 10.3.2 为什么要引入广义EM?
- 10.3.3 广义EM公式导出
- 10.3.4 广义EM有什么不同
- 10.4 EM算法变种
10 EM(期望最大)算法
10.1 背景介绍
概率图模型中,两个核心问题:学习参数、求解后验分布。EM算法就是一种通过MLE求出参数近似解的方法
10.2 EM算法公式
EM算法的具体公式表示为:
θ
(
t
+
1
)
=
a
r
g
max
θ
∫
Z
log
P
(
X
,
Z
∣
θ
)
⋅
P
(
Z
∣
X
,
θ
(
t
)
)
d
Z
=
a
r
g
max
θ
E
Z
∣
X
,
θ
(
t
)
[
log
P
(
X
,
Z
∣
θ
)
]
\begin{align} \theta^{(t+1)} & = arg\max_{\theta} \int_Z { \log{P(X, Z| \theta)} \cdot P(Z| X, \theta^{(t)}) } {\rm d}Z \\ & = arg\max_{\theta} E_{Z|X, \theta^{(t)}} [\log P(X, Z| \theta)] \end{align}
θ(t+1)=argθmax∫ZlogP(X,Z∣θ)⋅P(Z∣X,θ(t))dZ=argθmaxEZ∣X,θ(t)[logP(X,Z∣θ)]
其中上标中的
t
t
t和
t
+
1
t+1
t+1表示第
t
t
t、
t
+
1
t+1
t+1次迭代的参数结果,且参数满足:
X
=
{
x
i
}
i
=
1
N
X = {\lbrace x_i \rbrace}_{i=1}^N
X={xi}i=1N,
Z
=
{
z
i
}
i
=
1
N
Z = {\lbrace z_i \rbrace}_{i=1}^N
Z={zi}i=1N,且
z
z
z为离散分布:
| z z z | C 1 C_1 C1 | C 2 C_2 C2 | … \dots … | C k C_k Ck |
|---|---|---|---|---|
| P ( z ) P(z) P(z) | p 1 p_1 p1 | p 2 p_2 p2 | … \dots … | p k p_k pk |
且EM算法分为E-Step和M-Step:
-
E-Step——通过 t t t时刻的参数得到 t t t时刻的期望:
θ ( t ) → E Z ∣ X , θ ( t ) [ log P ( X , Z ∣ θ ) ] \theta^{(t)} \rightarrow E_{Z|X, \theta^{(t)}} [\log P(X, Z| \theta)] θ(t)→EZ∣X,θ(t)[logP(X,Z∣θ)] -
M-Step——将当前的最大期望作为移动方向求 t + 1 t+1 t+1时刻的参数:
θ ( t + 1 ) = a r g max θ E Z ∣ X , θ ( t ) [ log P ( X , Z ∣ θ ) ] \theta^{(t+1)} = arg\max_{\theta} E_{Z|X, \theta^{(t)}} [\log P(X, Z| \theta)] θ(t+1)=argθmaxEZ∣X,θ(t)[logP(X,Z∣θ)]
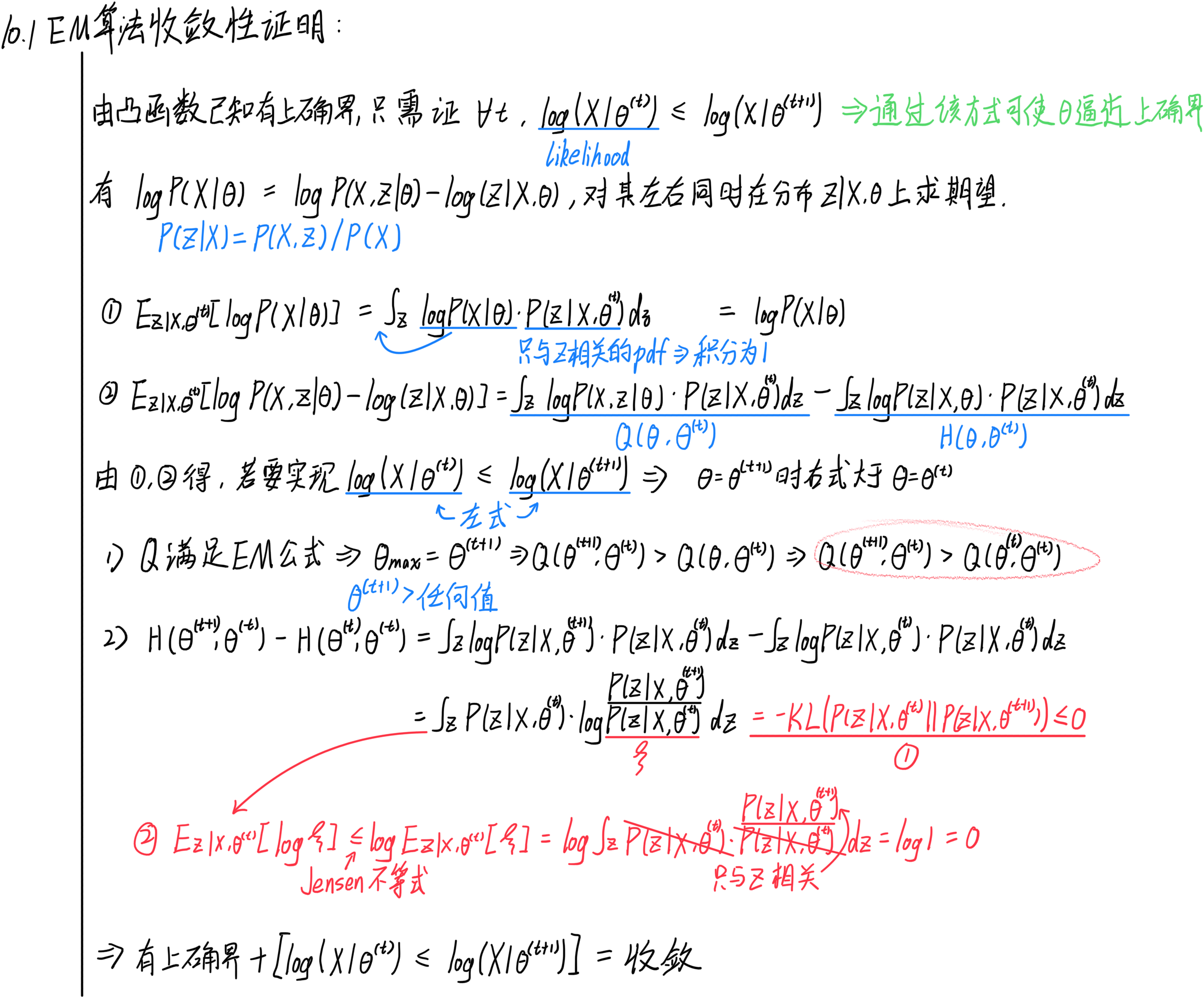
10.2.1 EM算法公式收敛性证明
若要用EM算法求解参数的近似解,我们需要证明EM算法公式是收敛的,以保证迭代结果离实际结果越来越近。
若要证明EM算法公式收敛,需要有以下条件:
- 该算法公式有上确界
- 每一次的迭代结果递增
证明过程如下:
总而言之:
- 要证明 log ( X ∣ θ ( t ) ) ≤ log ( X ∣ θ ( t + 1 ) ) \log(X|\theta^{(t)}) \leq \log(X|\theta^{(t+1)}) log(X∣θ(t))≤log(X∣θ(t+1)),可以将其看作 log ( X ∣ θ ) \log(X|\theta) log(X∣θ)在 t + 1 t+1 t+1时刻比 t t t时刻大
- 上文通过证明 log ( X ∣ θ ) \log(X|\theta) log(X∣θ)在 t + 1 t+1 t+1时刻减 t t t时刻的值 ≥ 0 \geq 0 ≥0,从而得出收敛性。
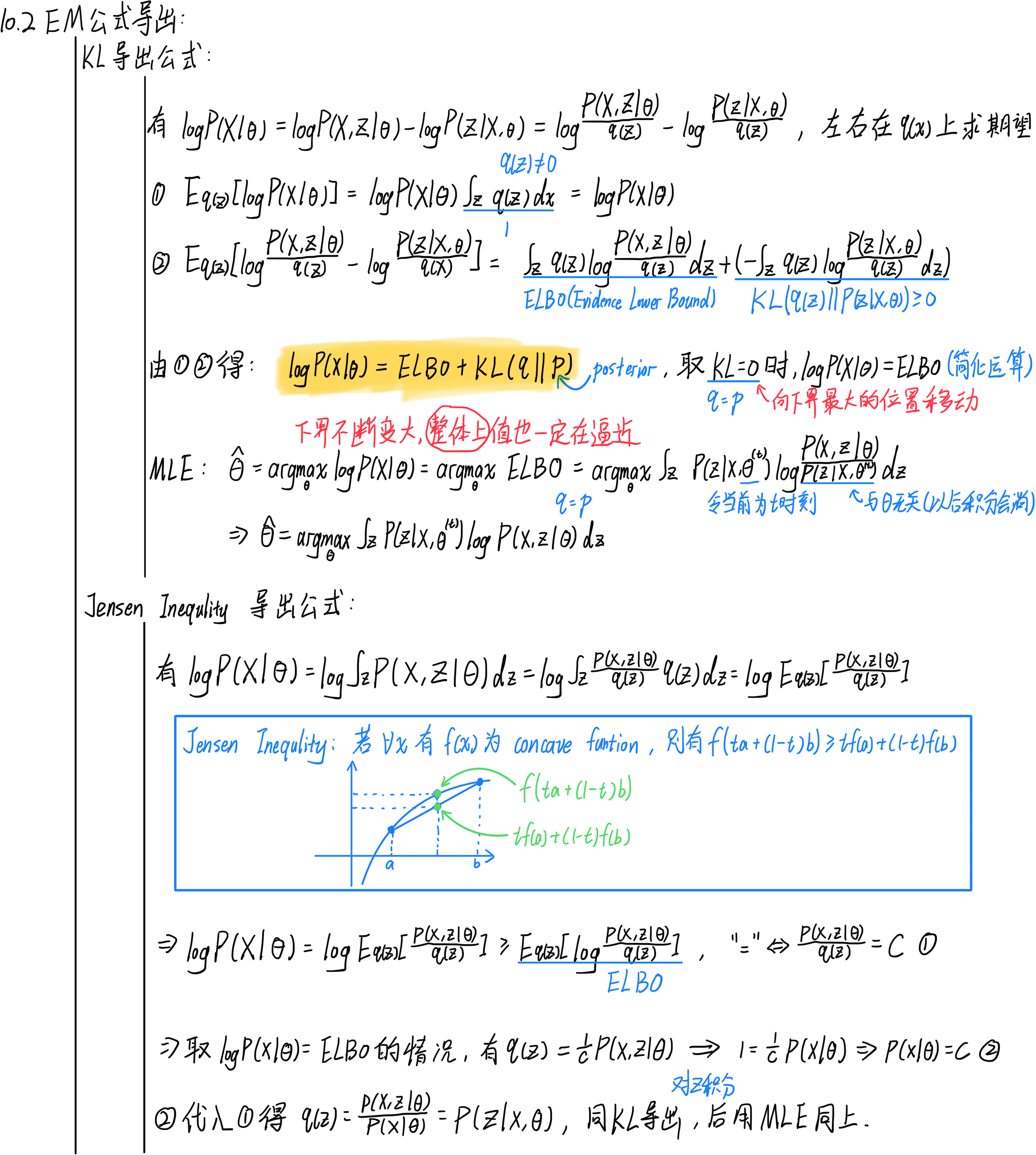
10.2.2 EM算法公式导出
下文通过两种方法将EM公式导出,核心思想很简单,就是分解likelihood:
10.3 广义EM算法
10.3.1 EM有什么作用?
- 能够解决概率生成模型。条件有 P ( X ∣ θ ) P(X|\theta) P(X∣θ)——likelihood、 X X X、 θ \theta θ时,EM用于估计 θ ^ \hat \theta θ^
- 具体通过引入隐变量Z,使得 P ( X ) = ∫ Z P ( X , Z ) d Z P(X) = \int_Z P(X, Z) {\rm d}Z P(X)=∫ZP(X,Z)dZ,然后用MLE求解
10.3.2 为什么要引入广义EM?
引入广义EM必然是因为狭义的EM有问题,狭义的EM可以写为:
{
E
−
S
t
e
p
:
q
^
=
P
(
Z
∣
X
,
θ
)
⟸
K
L
=
0
M
−
S
t
e
p
:
θ
(
t
+
1
)
=
a
r
g
max
θ
E
Z
∣
X
,
θ
(
t
)
[
log
P
(
X
,
Z
∣
θ
)
]
\begin{cases} E-Step: & {\hat q} = P(Z|X, \theta) \impliedby KL = 0 \\ M-Step: & \theta^{(t+1)} = arg\max_{\theta} E_{Z|X, \theta^{(t)}} [\log P(X, Z| \theta)] \end{cases}
{E−Step:M−Step:q^=P(Z∣X,θ)⟸KL=0θ(t+1)=argmaxθEZ∣X,θ(t)[logP(X,Z∣θ)]
从上面可以看出来我们引入了一个条件:
K
L
=
0
KL=0
KL=0,这个条件并不是很好用:
- 若非模型非常简单, q ^ = P ( Z ∣ X , θ ) {\hat q} = P(Z|X, \theta) q^=P(Z∣X,θ)实际上很难求解
- 所以 q ^ \hat q q^这个参数也需要通过别的方法求出近似解
10.3.3 广义EM公式导出
我们将EM公式重新拆分到优化前的状态:
log
P
(
X
∣
θ
)
=
L
(
q
,
θ
)
+
K
L
(
q
∣
∣
p
)
,
L
(
q
,
θ
)
=
E
L
B
O
\log P(X|\theta) = {\mathcal L}(q, \theta) + KL(q||p), \quad {\mathcal L}(q, \theta) = ELBO
logP(X∣θ)=L(q,θ)+KL(q∣∣p),L(q,θ)=ELBO
{ E L B O = E q ( Z ) [ log P ( X , Z ∣ θ ) q ( Z ) ] K L ( q ∣ ∣ p ) = ∫ q ( Z ) ⋅ log q ( Z ) P ( Z ∣ X , θ ) d Z \begin{cases} ELBO = E_{q(Z)} [\log \frac{P(X, Z|\theta)}{q(Z)}] \\ KL(q || p) = \int q(Z) \cdot \log \frac{q(Z)}{P(Z|X, \theta)} {\rm d}Z \end{cases} {ELBO=Eq(Z)[logq(Z)P(X,Z∣θ)]KL(q∣∣p)=∫q(Z)⋅logP(Z∣X,θ)q(Z)dZ
所以可以将计算在这里添加一步:
-
在 log P ( X ∣ θ ) = L ( q , θ ) + K L ( q ∣ ∣ p ) \log P(X|\theta) = {\mathcal L}(q, \theta) + KL(q||p) logP(X∣θ)=L(q,θ)+KL(q∣∣p)时固定 θ \theta θ(表示在同一个 θ \theta θ下),此时 log P ( X ∣ θ ) \log P(X|\theta) logP(X∣θ)为定值,得到:
q ^ = a r g min q K L ( q ∣ ∣ p ) = a r g max L ( q , θ ) {\hat q} = arg\min_q KL(q||p) = arg\max {\mathcal L}(q, \theta) q^=argqminKL(q∣∣p)=argmaxL(q,θ) -
求出了 q ^ {\hat q} q^后,固定 q ^ {\hat q} q^, log P ( X ∣ θ ) \log P(X|\theta) logP(X∣θ)依旧为定值,求:
θ ^ = a r g max θ L ( q ^ , θ ) {\hat \theta} = arg\max_{\theta} {\mathcal L}({\hat q}, \theta) θ^=argθmaxL(q^,θ)
于是就得到了广义EM的E-Step和M-Step:
{
E
−
S
t
e
p
:
q
(
t
+
1
)
=
a
r
g
max
q
L
(
q
,
θ
(
t
)
)
M
−
S
t
e
p
:
θ
(
t
+
1
)
=
a
r
g
max
θ
L
(
q
(
t
+
1
)
,
θ
)
\begin{cases} E-Step: & q^{(t+1)} = arg\max_q {\mathcal L}(q, \theta^{(t)}) \\ M-Step: & \theta^{(t+1)} = arg\max_{\theta} {\mathcal L}(q^{(t+1)}, \theta) \end{cases}
{E−Step:M−Step:q(t+1)=argmaxqL(q,θ(t))θ(t+1)=argmaxθL(q(t+1),θ)
形式上也可以写成下面这两步(也可以叫做MM算法):
{
M
1
−
S
t
e
p
:
q
(
t
+
1
)
=
a
r
g
max
q
L
(
q
,
θ
(
t
)
)
M
2
−
S
t
e
p
:
θ
(
t
+
1
)
=
a
r
g
max
θ
E
q
(
t
+
1
)
[
log
P
(
X
,
Z
∣
θ
)
]
\begin{cases} M_1-Step: & q^{(t+1)} = arg\max_q {\mathcal L}(q, \theta^{(t)}) \\ M_2-Step: & \theta^{(t+1)} = arg\max_{\theta} E_{q^{(t+1)}} [\log P(X, Z| \theta)] \end{cases}
{M1−Step:M2−Step:q(t+1)=argmaxqL(q,θ(t))θ(t+1)=argmaxθEq(t+1)[logP(X,Z∣θ)]
10.3.4 广义EM有什么不同
前后在计算上的差别就是期望的分布产生了变化:
E
Z
∣
X
,
θ
(
t
)
[
log
P
(
X
,
Z
∣
θ
)
]
⟹
E
q
(
t
+
1
)
[
log
P
(
X
,
Z
∣
θ
)
]
=
L
(
q
(
t
+
1
)
,
θ
)
E_{Z|X, \theta^{(t)}} [\log P(X, Z| \theta)] \implies E_{q^{(t+1)}} [\log P(X, Z| \theta)] = {\mathcal L}(q^{(t+1)}, \theta)
EZ∣X,θ(t)[logP(X,Z∣θ)]⟹Eq(t+1)[logP(X,Z∣θ)]=L(q(t+1),θ)
其实如果我们分解
L
(
q
,
θ
)
{\mathcal L}(q, \theta)
L(q,θ)可以得到:
L
(
q
,
θ
)
=
E
q
(
Z
)
[
log
P
(
X
,
Z
∣
θ
)
q
(
Z
)
]
=
E
q
(
Z
)
[
log
P
(
X
,
Z
∣
θ
)
]
−
E
q
(
Z
)
[
log
q
(
Z
)
]
{\mathcal L}(q, \theta) = E_{q(Z)} [ \log \frac{P(X,Z|\theta)}{q(Z)} ] = E_{q(Z)} [ \log P(X,Z|\theta) ] - E_{q(Z)} [ \log q(Z) ]
L(q,θ)=Eq(Z)[logq(Z)P(X,Z∣θ)]=Eq(Z)[logP(X,Z∣θ)]−Eq(Z)[logq(Z)]
我们发现广义的EM就是比狭义的EM多减去了一个
E
q
(
Z
)
[
log
q
(
Z
)
]
E_{q(Z)} [ \log q(Z) ]
Eq(Z)[logq(Z)],我们发现这就是熵的定义,且熵
H
[
q
(
Z
)
]
H[q(Z)]
H[q(Z)]与
θ
\theta
θ无关:
H
[
q
(
Z
)
]
=
E
q
(
Z
)
[
log
q
(
Z
)
]
H[q(Z)] = E_{q(Z)} [ \log q(Z) ]
H[q(Z)]=Eq(Z)[logq(Z)]
10.4 EM算法变种
EM算法无法解决一切问题,若有条件无法求解,就可能要用变分推断、蒙特卡洛等方法做近似估计。
所以变种有:VI/VB、VBEM/VEM,MCEM