本专栏包含信息论与编码的核心知识,按知识点组织,可作为教学或学习的参考。markdown版本已归档至【Github仓库:https://github.com/timerring/information-theory 】或者公众号【AIShareLab】回复 信息论 获取。
文章目录
- 信道的数学模型
- 广义信道的数学模型
- 连续信道的数学模型
- 离散信道数学模型
- 半连续信道
信道的数学模型
广义信道的数学模型
连续信道模型 和 离散信道模型
连续信道的数学模型
广义信道中的调制信道属于连续信道。我们所关心的是信号经过信道所得到的输出信号,信道内部的变化过程并不重要。可以用描述一定输入、输出关系的方框来表示。

连续信道具有以下一些特征:
- 可以有一对或者多对输入端和输出端;
- 大多数信道都为线性,也就是满足线性叠加原理;
- 信号通过此类信道具有固定或者时变延迟,以及固定或时变的损耗和衰落;
- 信道中不可避免的会引入噪声,即使没有输入信号,也会有噪声输出。

连续信道一般可以看作一个输出端叠加有噪声的时变线性网络,输入输出关系如下:
r
(
t
)
=
f
[
s
i
(
t
)
]
+
n
(
t
)
r(t)=f\left[s_{i}(t)\right]+n(t)
r(t)=f[si(t)]+n(t)
其中:
$ s_{i}(t)$ 是输入的连续信号, r ( t ) r(t) r(t) 是信道总的输出, n ( t ) n(t) n(t) 是加性噪声;
n ( t ) n(t) n(t) 独立于 s i ( t ) s_{i}(t) si(t) 。
s
o
(
t
)
=
f
[
s
i
(
t
)
]
s_{o}(t)=f[s_{i}(t)]
so(t)=f[si(t)] 实际反映了物理信道的特性,
f
[
s
i
(
t
)
]
f[s_{i}(t)]
f[si(t)] 可以表示成信道单位冲激响应与输入信号的卷积, 也即
f
[
s
i
(
t
)
.
]
f[s_{i}(t). ]
f[si(t).]反映信道的特性, 可以表示为:
s
0
(
t
)
=
f
[
s
i
(
t
)
]
=
h
(
t
)
∗
s
i
(
t
)
S
o
(
f
)
=
H
(
f
)
S
i
(
f
)
s_{0}(t)=f[s_{i}(t)]=h(t) * s_{i}(t) \\ \boldsymbol{S}_{\boldsymbol{o}}(\boldsymbol{f})=\boldsymbol{H}(\boldsymbol{f}) \boldsymbol{S}_{\boldsymbol{i}}(\boldsymbol{f})
s0(t)=f[si(t)]=h(t)∗si(t)So(f)=H(f)Si(f)
$ H(f) $依赖于信道的特性, 可以看成是乘性千扰。
讨论:
1)连续信道对信号的干扰主要有两种 乘性干扰 ℎ(𝑡)和加性干扰 𝑛(𝑡),分析信道对信号的具体影响,只要了解 ℎ(𝑡)与 𝑛(𝑡)的特性即可。
2)分析乘性干扰 ℎ(𝑡)的影响时,可以把连续信道分成两大类:
- 恒参信道,即 ℎ(𝑡)随时间缓变或者不变;通常将架空明线、电缆、光导纤维、超短波及微波视距传播、卫星中继等看作恒参信道。
- 是随参信道,即 ℎ(𝑡)随机快变化。短波电离层反射信道、各种散射信道、超短波移动通信信道等可以视为随参信道。
离散信道数学模型
广义信道中的编码信道就是一种离散信道(数字信道)。离散信道的输入变量 X 、输出变量 Y 均为离散信号(数字信号)。信道的特性可用信道转移概率(条件概率)来描述。主要研究离散信号在信道中传输的特征。
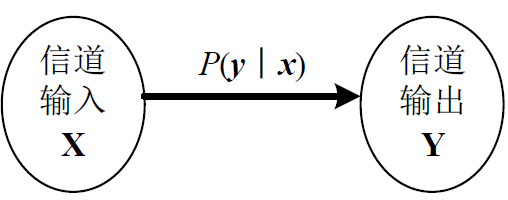
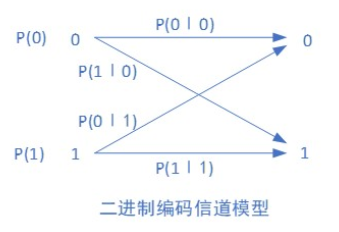
例:二进制无记忆编码信道(BSC)
p ( 0 / 0 ) p(0 / 0) p(0/0) 和 p ( 1 / 1 ) p(1 / 1) p(1/1) 为正确转移概率, p ( 1 / 0 ) p(1 / 0) p(1/0) 和 p ( 0 / 1 ) p(0 / 1) p(0/1) 为错误转移概率 , 我们有 p ( 0 / 0 ) = 1 − p ( 1 / 0 ) p(0 / 0)=1-p(1 / 0) p(0/0)=1−p(1/0) ; p ( 1 / 1 ) = 1 − p ( 0 / 1 ) p(1 / 1)=1-p(0 / 1) p(1/1)=1−p(0/1) 。
半连续信道
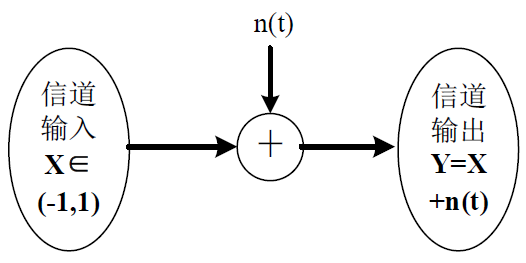
输入变量 X 和输出变量 Y 一个为连续信号,一个为离散信号。如下图所示的 AWGN 信道,输入是二进制对极信号,输出是叠加了高斯白噪声的连续信号。
参考文献:
- Proakis, John G., et al. Communication systems engineering. Vol. 2. New Jersey: Prentice Hall, 1994.
- Proakis, John G., et al. SOLUTIONS MANUAL Communication Systems Engineering. Vol. 2. New Jersey: Prentice Hall, 1994.
- 周炯槃. 通信原理(第3版)[M]. 北京:北京邮电大学出版社, 2008.
- 樊昌信, 曹丽娜. 通信原理(第7版) [M]. 北京:国防工业出版社, 2012.