【HDU No. 4417】 超级马里奥 Super Mario

杭电OJ 题目地址

【题意】

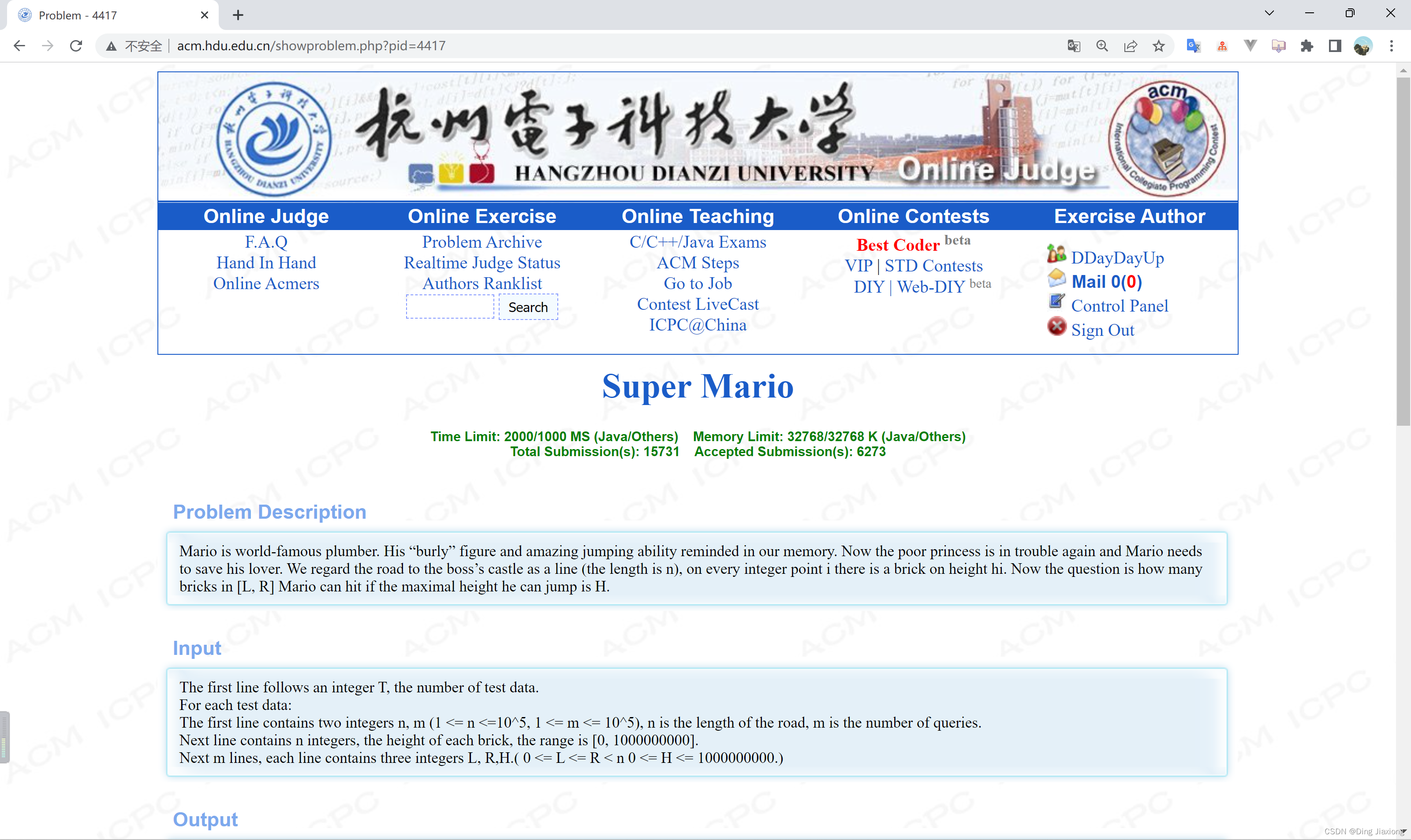
可怜的公主陷入困境，马里奥需要拯救他的情人。把通往城堡的道路视为一条线（长度为n ），在每个整数点i 上都有一块高度为hi 的砖，马里奥可以跳的最大高度是H ，求他在[L , R ]区间可以跳过多少砖块。

【输入输出】

输入：

第1行是整数T，表示测试用例的数量。每个测试用例的第1行都包含两个整数n、m （1≤n ，m ≤10^5 ），n 是道路的长度，m 是查询的数量。下一行包含n 个整数，表示每个砖的高度（范围是[0,10^9 ]）。接下来的m 行，每行都包含三个整数L 、R 、H （0≤L ≤R<n ，0≤H ≤10^9 ）。

输出：

对每种情况都输出“Case X ：”（X 是从1开始的案例编号），后跟m 行，每行都包含一个整数。第i 个整数是第i 个查询中马里奥跳过的砖块数。

【样例】

【思路分析】

这道题也是区间查询问题，查询[l , r ]区间小于或等于h 的元素个数，可以采用分块的方法解决。

【算法设计】

① 分块。划分块并对每一块进行非递减排序。在辅助数组temp[]上排序，原数组不变。

② 查询。查询[l , r ]区间小于或等于h 的元素个数。

• 若该区间属于同一块，则暴力累加块内小于或等于h 的元素个数。
• 若该区间包含多个块，则累加中间每一块小于或等于h 的元素个数，此时可以用upper_bound()函数统计，然后暴力累加左端和右端小于或等于h 的元素个数。

【举个栗子】

根据测试用例的输入数据，分块算法的求解过程如下。

① 分块。n =10，t = √n =3，每3个元素为一块，一共分为4块，最后一块只有一个元素。原数组a []和每一块排序后的辅助数组temp[]如下图所示。

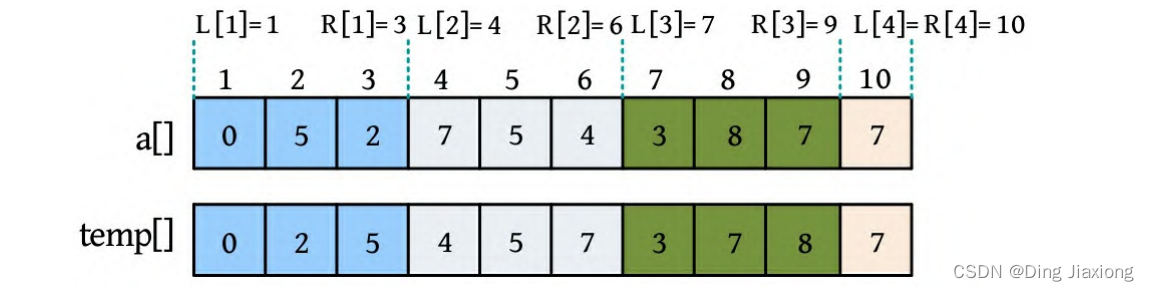
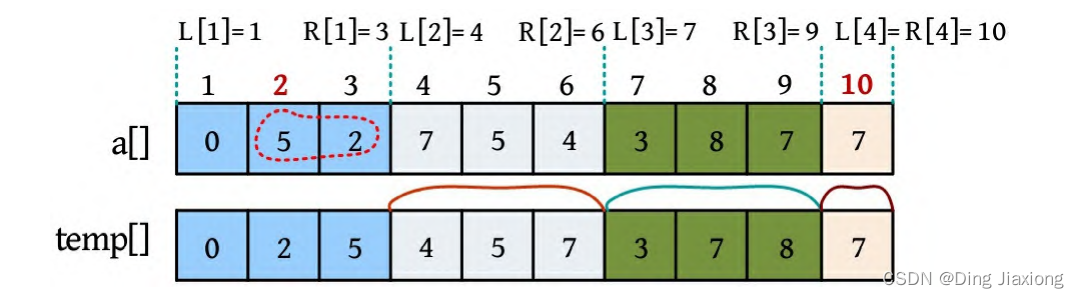
② 查询。1 9 4：因为题目中的下标从0开始，上图中的下标从1开始，所以实际上是查询[2, 10]区间高度小于或等于4的元素个数。[2, 10]区间跨4个块，左端第1个块没有完全包含，需要暴力统计a[2]、a [3]小于或等于4的元素。

后面3个块是完整的块，对完整的块可以直接用upper_bound()函数在temp数组中统计，该函数利用有序性进行二分查找，效率较高。

【算法实现】

upper_bound( begin, end, num)：从数组的begin位置到end-1位置二分查找第1个大于num的数字，若找到，则返回该数字的地址，否则返回end。将返回的地址减去起始地址begin，即可得到小于或等于num的元素个数。

#include<cstdio>
#include<cstring>
#include<algorithm>//sort 
#include<cmath>//sqrt

using namespace std;

const int maxn=1e5+10;
int L[maxn],R[maxn],belong[maxn];
int a[maxn],temp[maxn],n,m;

void build(){
    int t=sqrt(n);
    int num=n/t;
	if(n%num) num++;
    for(int i=1;i<=num;i++)
        L[i]=(i-1)*t+1,R[i]=i*t;
    R[num]=n;
    for(int i=1;i<=n;i++)
        belong[i]=(i-1)/t+1;
    for(int i=1;i<=num;i++)
        sort(temp+L[i],temp+1+R[i]);//每块排序
}

int query(int l,int r,int h){
    int ans=0;
    if(belong[l]==belong[r]){
        for(int i=l;i<=r;i++)
            if(a[i]<=h) ans++;
    }
    else{
        for(int i=l;i<=R[belong[l]];i++)//左端 
            if(a[i]<=h) ans++;
        for(int i=belong[l]+1;i<belong[r];i++)//中间 
            ans+=upper_bound(temp+L[i],temp+R[i]+1,h)-temp-L[i];
        for(int i=L[belong[r]];i<=r;i++)//右端 
            if(a[i]<=h) ans++;
    }
    return ans;
}

int main(){
	
    int T;
    scanf("%d",&T);
    for(int cas=1;cas<=T;cas++){
        scanf("%d%d",&n,&m);
        for(int i=1;i<=n;i++){
            scanf("%d",&a[i]);
            temp[i]=a[i];
        }
        build();
        printf("Case %d:\n",cas);
        while(m--){
            int l,r,h; 
            scanf("%d%d%d",&l,&r,&h);
            printf("%d\n",query(++l,++r,h));
        }
    }
	
    return 0;
}