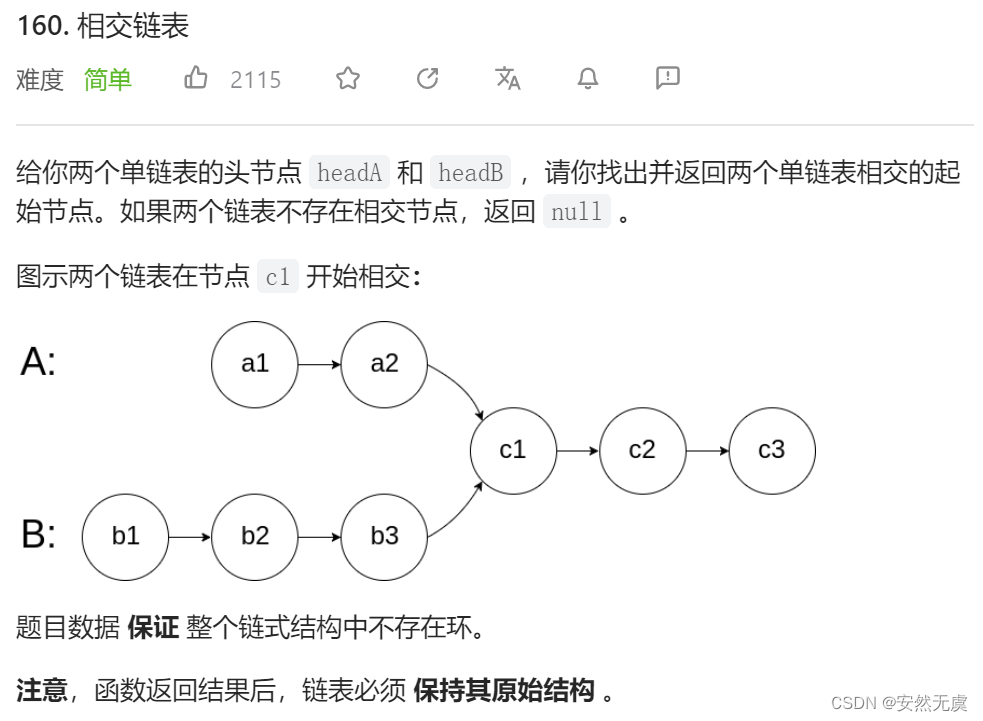
学习数据结构与算法的目的：
$$优化时间复杂度与空间复杂度$$
教程总纲： 暴力解法(模拟)、算法优化(递归/二分/排序/DP)、时刻转换(数据结构)

1.时间复杂度的核心方法论

空间是廉价的，时间是昂贵的

相较于空间复杂度(投入金钱 增加算力)，时间复杂度(消耗时间)更为重要！

降低时间与空间复杂度的方法：

时刻转换：选用合适的数据结构，进一步降低时间复杂度

例.输入数组 a = [1,2,3,4,5,5,6] 中查找出现次数最多的数值。

暴力解法是：两层for遍历，维护一个最大次数time_max，对每个元素计算出现次数time_tmp，与time_max进行对比，时间复杂度是 $0(n^2)$

int main(){
	vector<int> a={1,2,3,4,5,5,6};
	int val_max=-1,time_max=0,time_tmp=0;
	for(int i=0;i<a.size();i++){
		time_tmp=0;
		for(int j=0;j<a.size();j++)
			if(a[i]==a[j]) time_tmp++;
		if(time_tmp>time_max){
			time_max=time_tmp;
			val_max=a[i];
		}
	}
	cout<<val_max<<" "<<time_max<<endl;
	return 0;
}

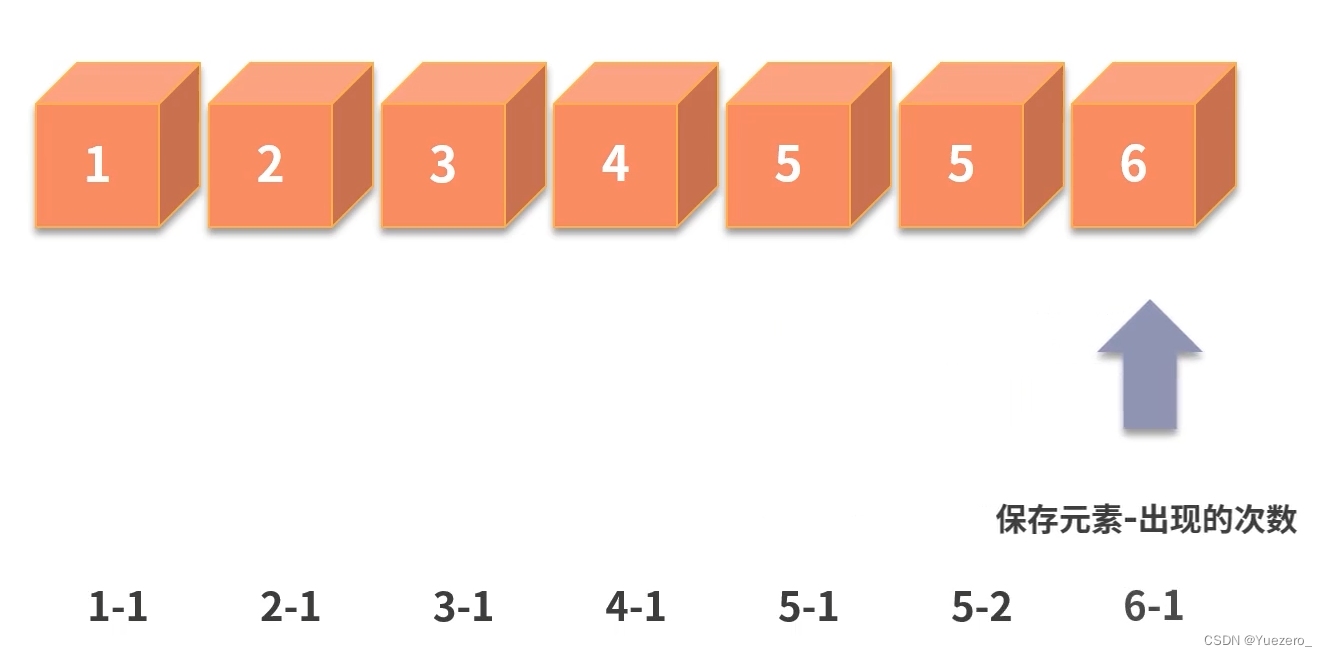
优化思想：如何仅用单层for循环完成，用hash思想，引入k-v字典数据结构map，一次for保存每个元素出现的次数，再求每个元素次数的最大值，时间复杂度是$0(2n)$。

int main(){
	vector<int> a={1,2,3,4,5,5,6};
    map<int ,int> num_cnt;
    int val_max,time_max=0;
	for(int i=0;i<a.size();i++){
		num_cnt[a[i]]++; //counting the number of times a[i occurs in the vector a.
	}
    for(auto it:num_cnt){ //iterating over the map and printing the max time a[i] occurs for each element.  
        if(time_max < it.second){
            val_max=it.first; //assigning the maximum value from the map to val_max.
            time_max=it.second; //assigning the maximum count from the map to time_max.
        }
    }
	cout<<val_max<<" "<<time_max<<endl;
	return 0;
}

2.增删查——选取数据结构的基本方法

当你不知道用什么数据结构的时候：
$$分析需要对数据进行了哪些操作，根据数据操作，选取合适的数据结构$$

还用上面的例子介绍：

对于统计次数最多的元素，我们需要对数据结构进行以下操作：

具体的：

所以

3.线性表——如何完成基本增删查

实际上，有线性存储(数组)和链式存储(链表)两种结构，这里仅介绍链式存储。

单向链表：

循环链表：

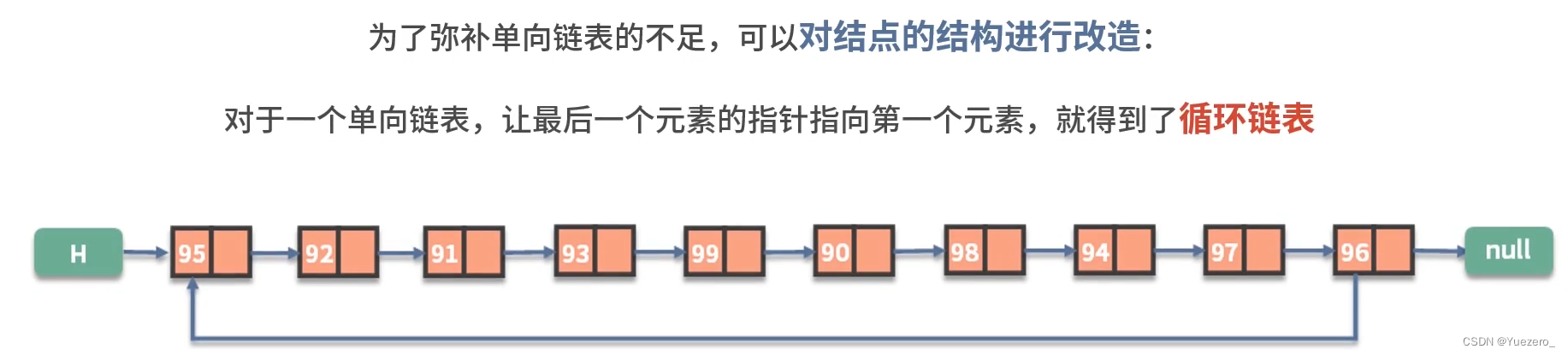
双向链表：

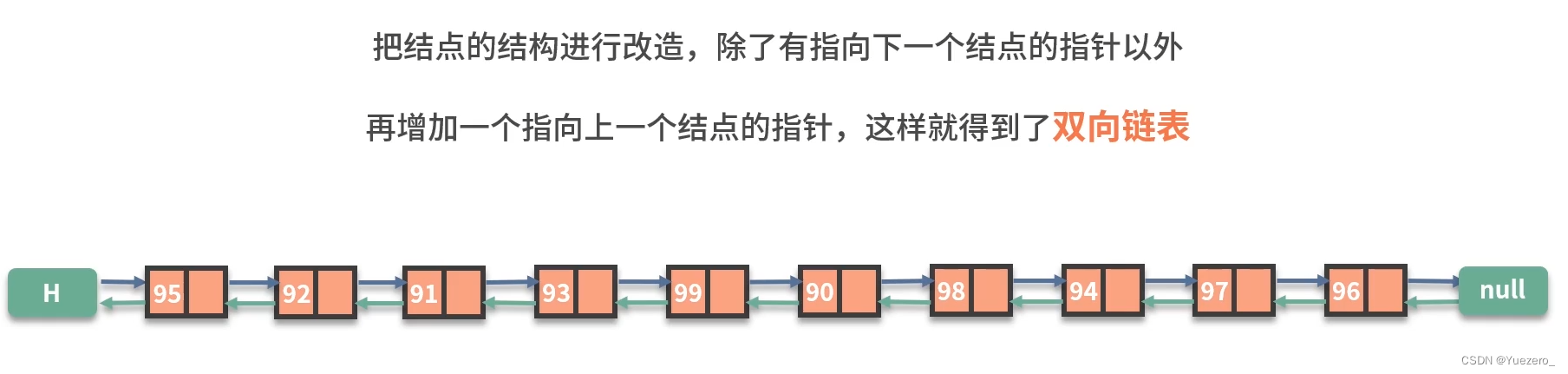
双向循环链表：

线性表增删查：其他链表的操作与单向链表雷同，仅介绍单向链表

增加操作：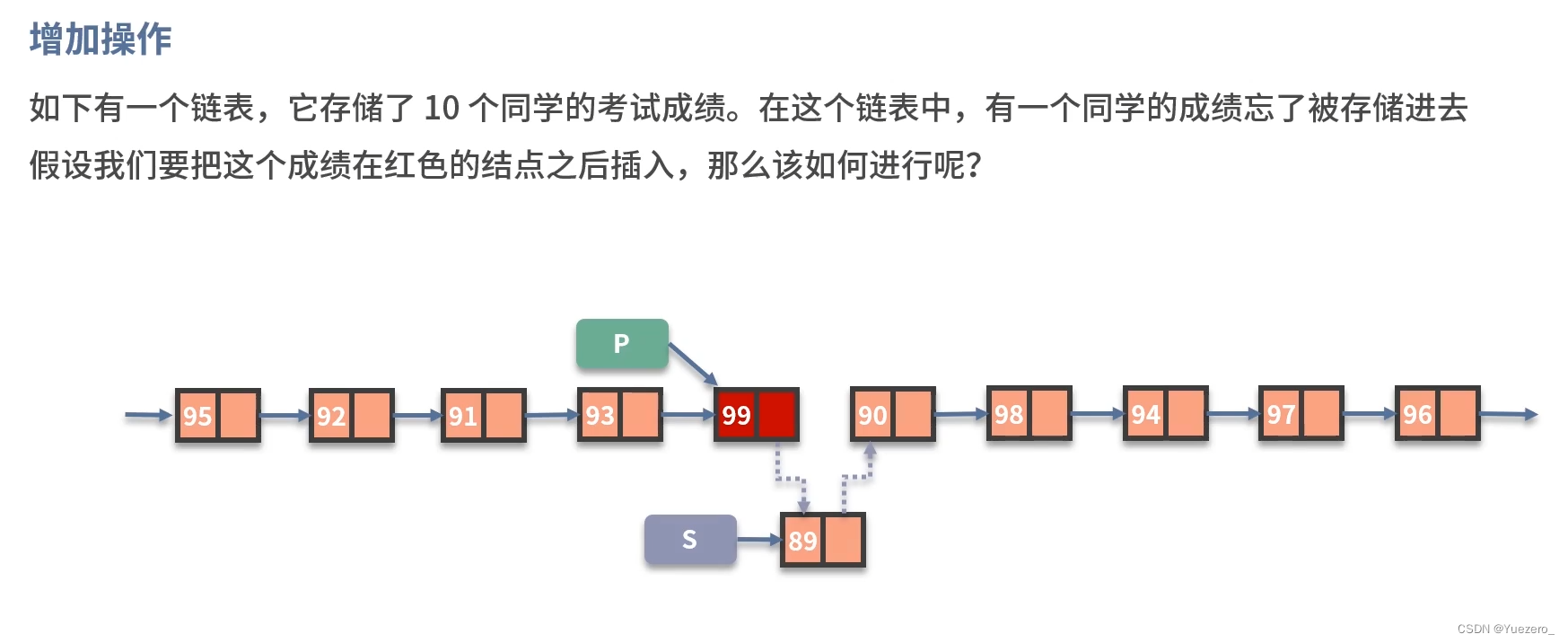
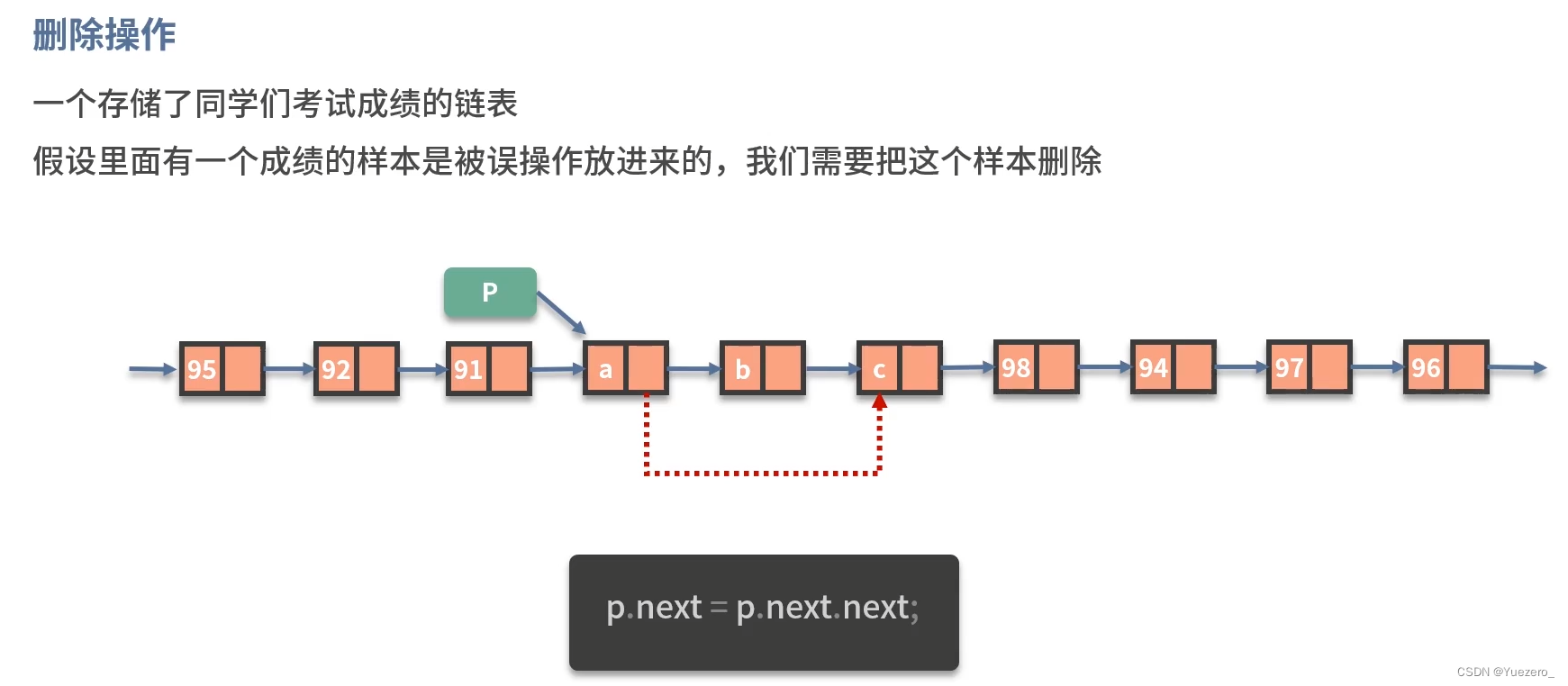
删除操作：

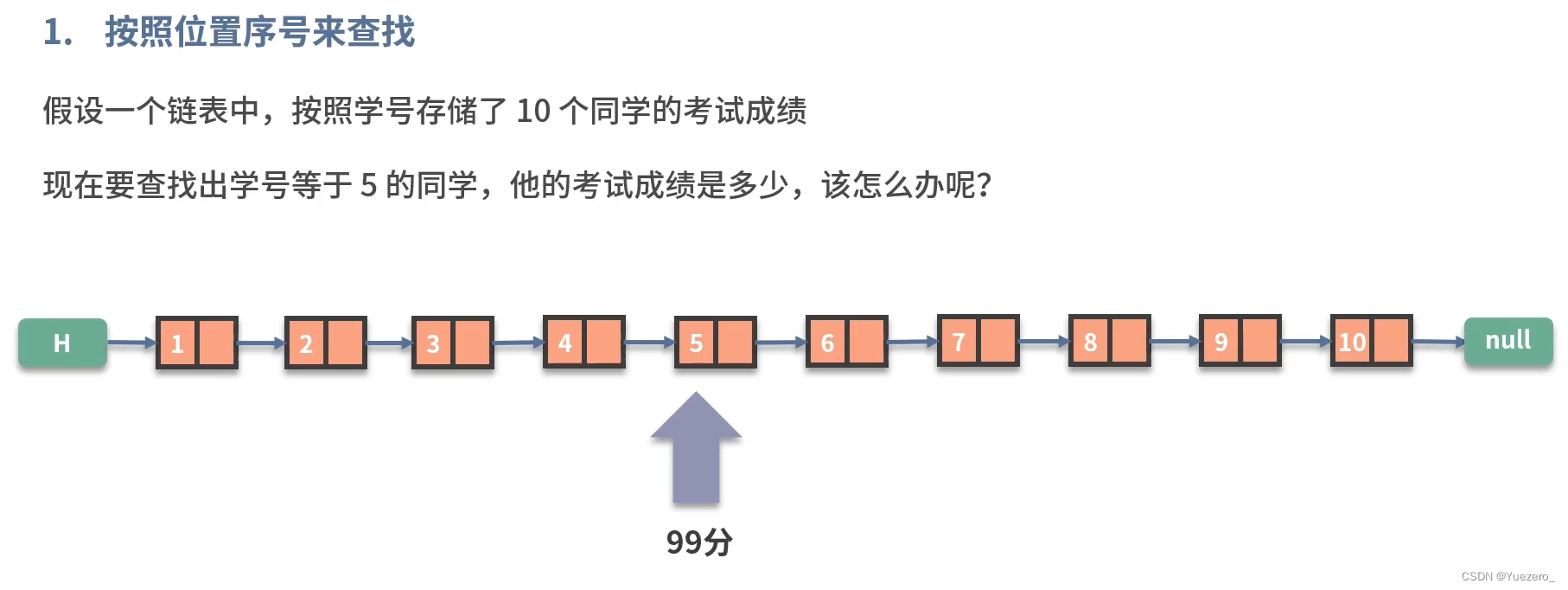
查找操作：


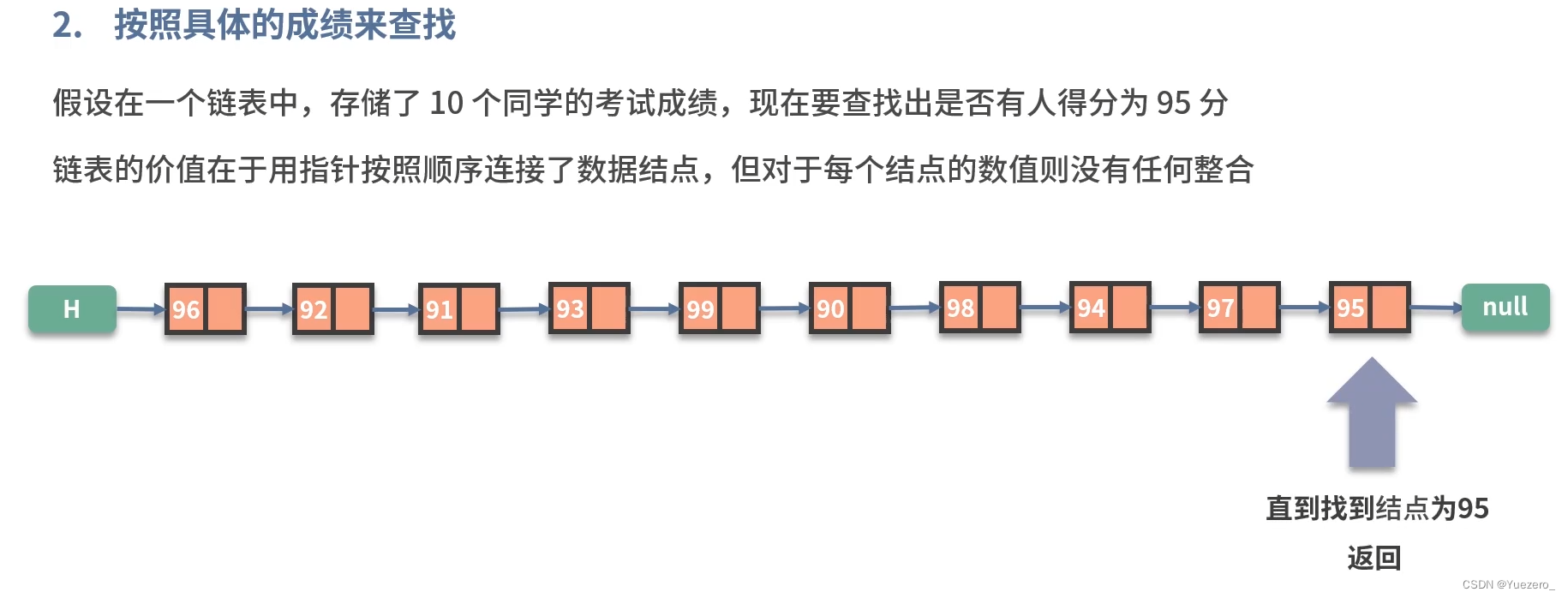
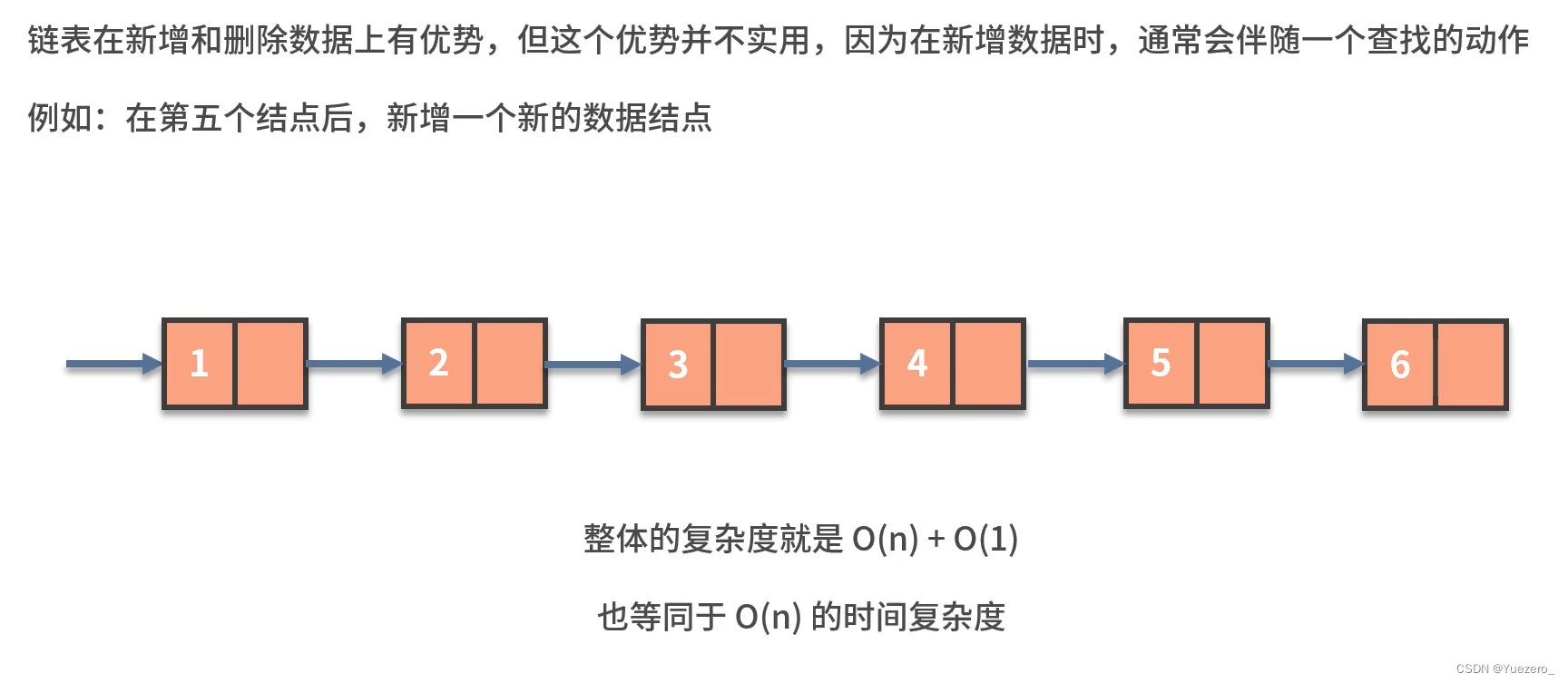
总结：
$$链表的查找速度慢(无法用index)O(n)，但插入和删除(改变指针)方便O(1)$$

链表的问题常常围绕数据顺序的处理：链表反转，快慢指针

为此，我们使用3个指针prev、curr、next，分别指向 新链表头节点、旧链表转换节点、旧链表转换节点的下一个，完成旧链表向链表逐个节点的转换。

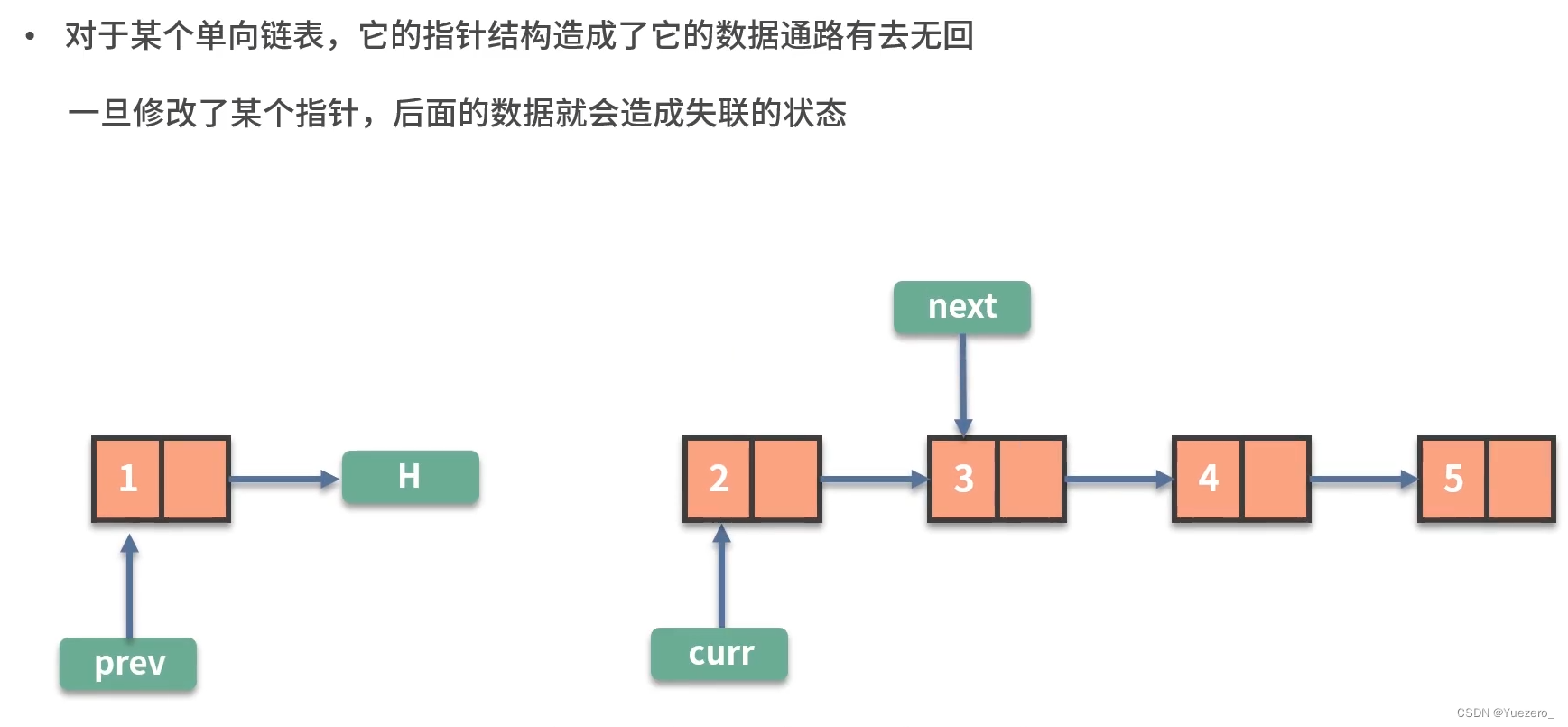
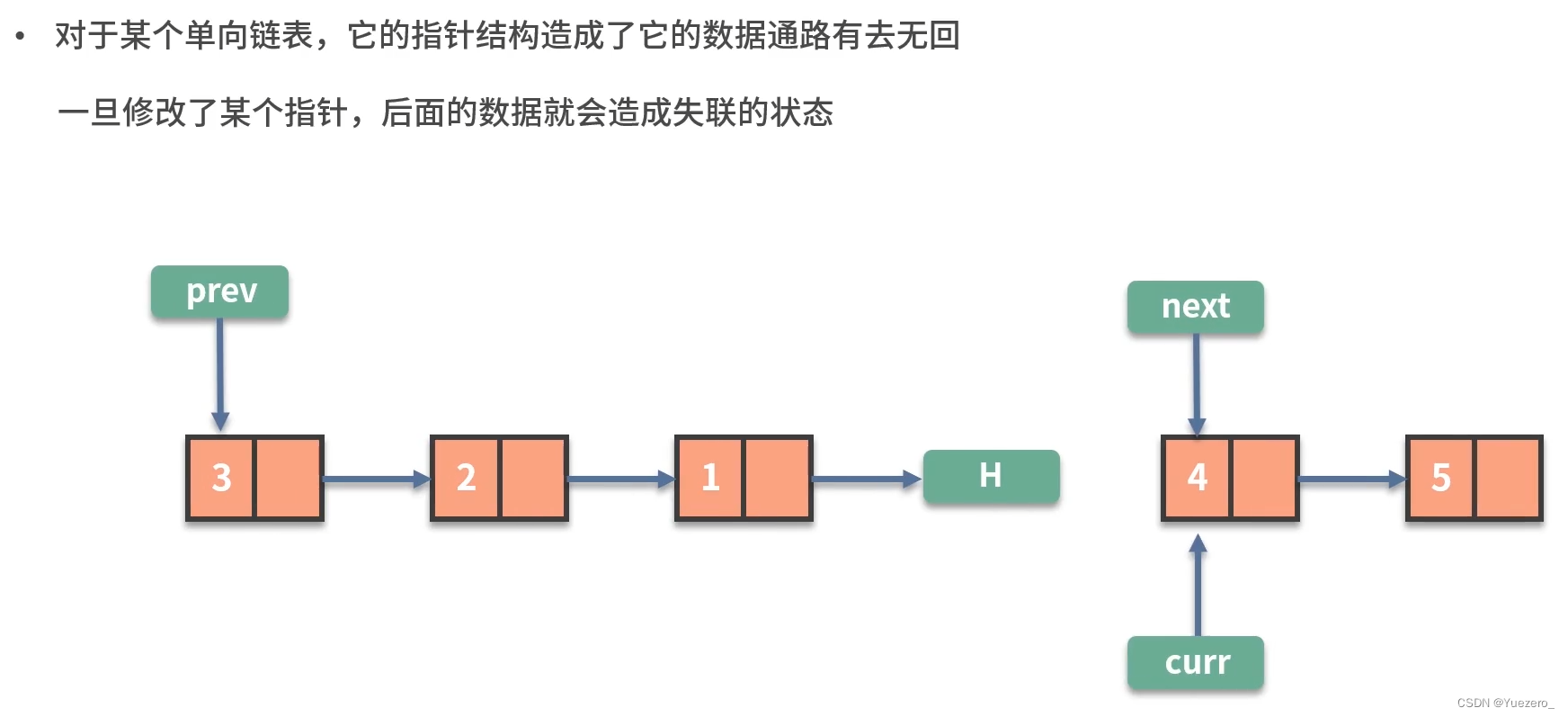
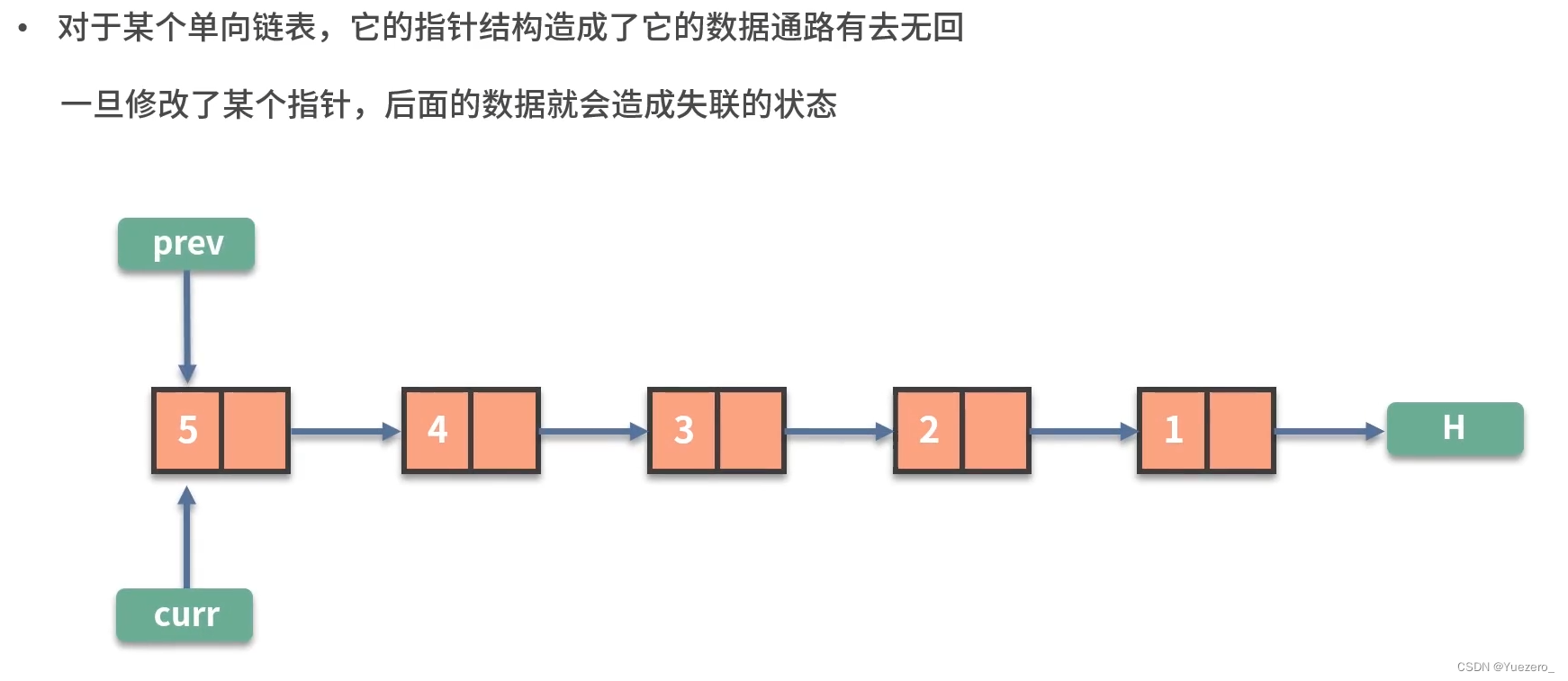
#include<bits/stdc++.h>
using namespace std;
#define rep(i,s,e) for(int i=s;i<e;i++)
#define per(i,s,e) for(int i=s;i>e;i--)

struct node{
    int data=0;
    node* next;
};

int main(){
    node*head=new node,*n1=new node,*n2=new node,*n3=new node;
    head->data=0;
    head->next=n1; n1->data=1; n1->next=n2; n2->data=2; n2->next=n3; n3->data=3;n3->next=NULL;
    node*tmp=head;
    //输出原链表
    while(tmp!=NULL){
        cout<<tmp->data<<" ";
        tmp=tmp->next;
    }cout<<endl;

    node* curr=head,*prev=head,*next=head->next;
    head->next=NULL;
    while(next!=NULL){
        curr=next; next=next->next;
        curr->next=prev; prev=curr;
    }
    //输出逆序链表
    while(curr!=NULL){
        cout<<curr->data<<" ";
        curr=curr->next;
    }
	return 0;
}

/*
0 1 2 3 
3 2 1 0
*/

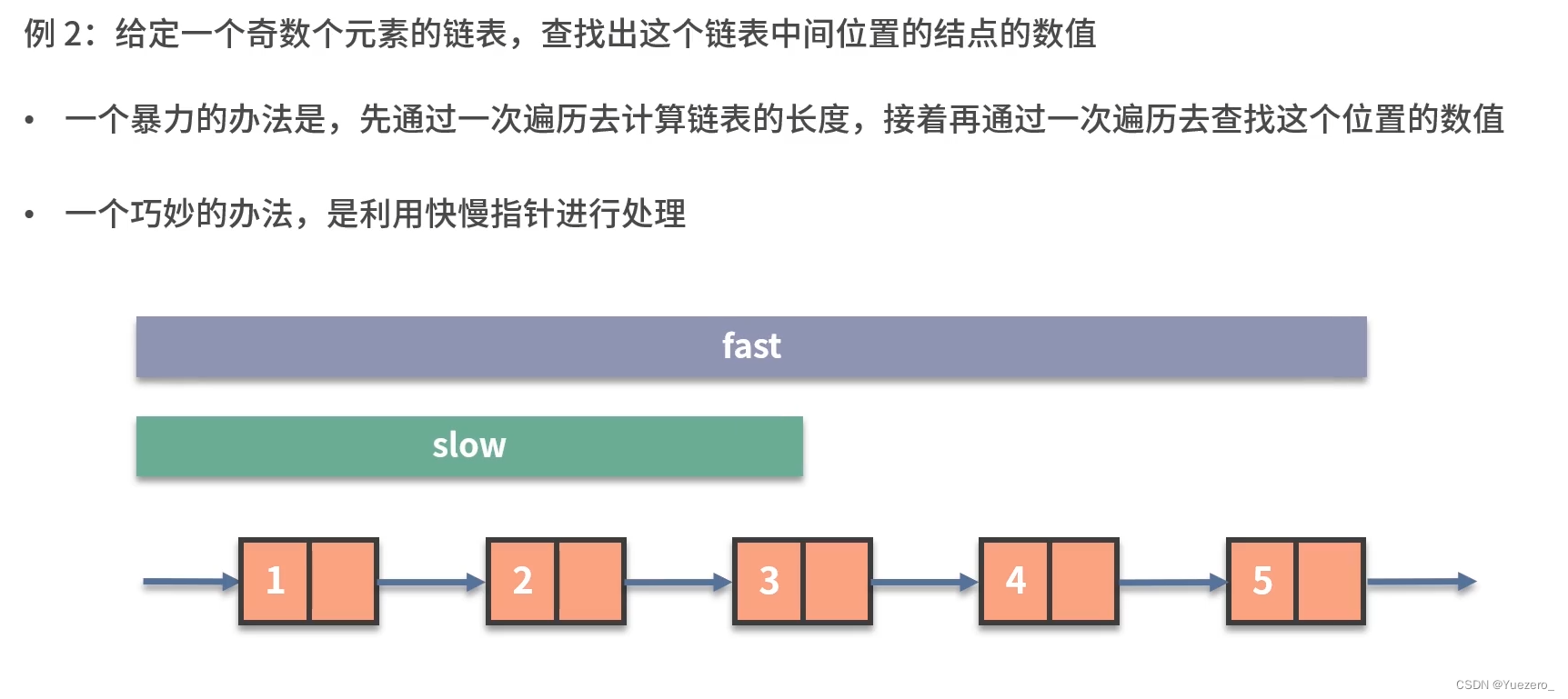
slow走1步，fast走两步。
fast到达终点时，slow到达中点。

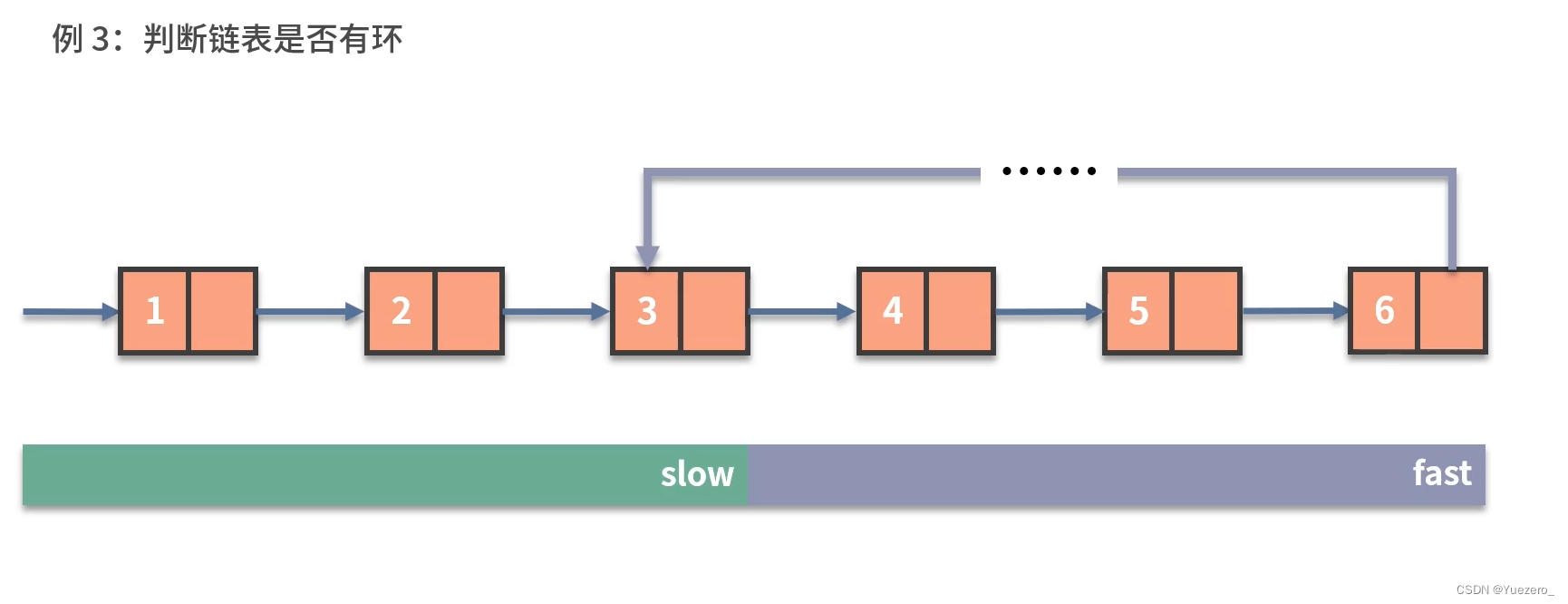
如果有环，2个指针一定会在环内相遇，fast=slow。