文章目录
- 【1. 独立】
- 【2. 相关】
- 【3.正交】
- 【4. 相互关系】
- 相关和独立
- 相关和正交
- 独立和正交
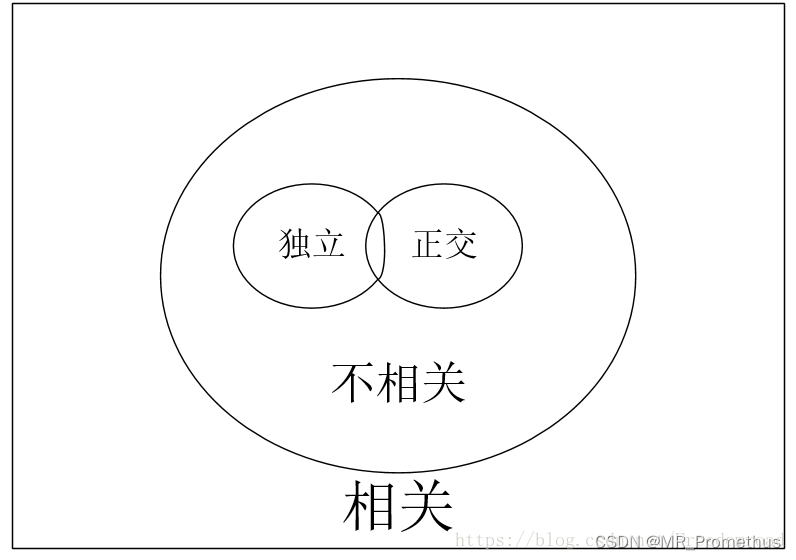
- 独立、不相关和正交
- 小结
- 【5. 参考文献】
【1. 独立】
- 独立:对于两个随机变量 y 1 y_1 y1 和 y 2 y_2 y2,若 y 1 y_1 y1 的有关信息不给出 y 2 y_2 y2 的任何信息,并且 y 2 y_2 y2 的有关信息也不包含有 y 1 y_1 y1 的任何信息,则称这两个随机变量独立,并有 P ( y 1 , y 2 ) = P ( y 1 ) P ( y 2 ) P(y_1,y_2)=P(y_1)P(y_2) P(y1,y2)=P(y1)P(y2)其中 P ( y 1 , y 2 ) P(y_1,y_2) P(y1,y2) 是 y 1 y_1 y1 和 y 2 y_2 y2 联合概率密度函数, P ( y 1 ) {P(y}_1) P(y1), P ( y 1 ) {P(y}_1) P(y1) 分别是 y 1 y_1 y1 和 y 2 y_2 y2 的边缘概率密度函数。
- 独立刻画的是两个变量之间是否存在联系。
- 若
y
1
y_1
y1 和
y
2
y_2
y2 是两个独立的随机变量,且
h
1
(
y
1
)
h_1(y_1)
h1(y1) 和
h
2
(
y
2
)
h_2(y_2)
h2(y2) 分别是
y
1
y_1
y1 和
y
2
y_2
y2 的函数,则:
E { h 1 ( y 1 ) h 2 ( y 2 ) } = E { h 1 ( y 1 ) } E { h 2 ( y 2 ) } E\{h_1(y_1)h_2(y_2)\}=E\{h_1(y_1)\}E\{h_2(y_2)\} E{h1(y1)h2(y2)}=E{h1(y1)}E{h2(y2)} - 当
y
1
y_1
y1 和
y
2
y_2
y2 相互独立时,协方差为 0。
cov ( y 1 , y 2 ) = E ( [ y 1 − E ( y 1 ) ] [ y 2 − E ( y 2 ) ] ) = 0 \operatorname{cov}(\mathrm y_1,\mathrm y_2)=\operatorname E([\mathrm y_1-\mathrm E(\mathrm y_1)][\mathrm y_2-\mathrm E(\mathrm y_2)])=0 cov(y1,y2)=E([y1−E(y1)][y2−E(y2)])=0
【2. 相关】
- 相关:如果存在一组不全为零的数 c 1 , c 2 . . . , c m ∈ K c_1,c_2...,c_m∈K c1,c2...,cm∈K,使得对于元素 x 1 , x 2 . . . , x m ∈ V x_1,x_2...,x_m∈V x1,x2...,xm∈V 有 ∑ i = 1 m c i x i = 0 \sum_{i=1}^{m}c_ix_i=0 ∑i=1mcixi=0 ,则称元素组 x 1 , x 2 . . . , x m x_1,x_2...,x_m x1,x2...,xm 线性相关,否则称其线性无关(即:系数不全为0的线性组合为0,则元素组线性相关)。
- X和Y不相关,意味着两者不存在线性关系,但是不能保证也没有非线性的关系。
- 当
y
1
y_1
y1 和
y
2
y_2
y2 不相关时,协方差为 0。
cov ( y 1 , y 2 ) = E ( [ y 1 − E ( y 1 ) ] [ y 2 − E ( y 2 ) ] ) = 0 \operatorname{cov}(\mathrm y_1,\mathrm y_2)=\operatorname E([\mathrm y_1-\mathrm E(\mathrm y_1)][\mathrm y_2-\mathrm E(\mathrm y_2)])=0 cov(y1,y2)=E([y1−E(y1)][y2−E(y2)])=0
【3.正交】
- 正交:若 y 1 y_1 y1 不含有 y 2 y_2 y2 的任何成分, y 2 y_2 y2 也不含有 y 1 y_1 y1 的任意成分,则称两个随机变量 y 1 y_1 y1 与 y 2 y_2 y2 正交,数学上定义为 E { y 1 y 2 } = 0 E\{y_1y_2\}=0 E{y1y2}=0 。
- 正交信号的性质:互相关函数恒等于0,内积为0。
【4. 相互关系】
相关和独立
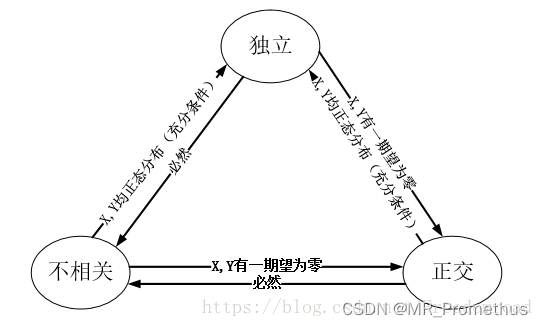
- 独立一定不相关,不相关不一定独立。
- 唯一的例外是高斯随机过程:任意两个高斯随机过程的统计不相关和统计独立是等价的。
举例不相关不一定独立:令 Y = X 2 , X ∈ [ − 1 , 0 , 1 ] , Y ∈ [ 1 , 0 , 1 ] Y=X^2,\quad X\in[-1,0,1],\quad Y\in[1,0,1] Y=X2,X∈[−1,0,1],Y∈[1,0,1],其中,X的三种取值等概率。
- X,Y 不相关:
E ( X Y ) − E ( X ) E ( Y ) = 0 − 0 × 2 3 = 0 E(X Y)-E(X)E(Y)=0-0\times{\frac{2}{3}}=0 E(XY)−E(X)E(Y)=0−0×32=0- X,Y不独立:
P ( X ≤ 0 , Y ≤ 0 ) = 1 3 P ( X ≤ 0 ) P ( Y ≤ 0 ) = 2 3 × 1 3 = 2 9 ≠ 1 3 \begin{aligned} &P(X\leq0,Y\leq0)={\frac{1}{3}} \\ &P(X\leq0)P(Y\leq0)={\frac{2}{3}}\times{\frac{1}{3}}={\frac{2}{9}}\neq{\frac{1}{3}} \end{aligned} P(X≤0,Y≤0)=31P(X≤0)P(Y≤0)=32×31=92=31
相关和正交
- 正交一定不相关,不相关不一定正交
- 若x(t)和y(t)的均值均等于零,则不相关与正交彼此等价。
举例不相关不一定正交: X = [ 0 , 1 , 1 ] , Y = [ 1 , 0 , 1 ] X=[0,1,1],Y=[1,0,1] X=[0,1,1],Y=[1,0,1]
- X,Y 不相关:
显然。- X,Y不正交:
X ⋅ Y = 0 × 1 + 1 × 0 + 1 × 1 = 1 ≠ 0 X·Y=0\times1+1\times 0+1\times 1=1\neq0 X⋅Y=0×1+1×0+1×1=1=0
独立和正交
独立、不相关和正交
- 零均值的高斯信号的独立、不相关和正交三者等价。
小结
- 不相关包括独立和正交两种。
【5. 参考文献】
[1] 张贤达. 现代信号处理[M]. 清华大学出版社, 2002.
[2]