647. 回文子串

教程视频：https://www.bilibili.com/video/BV17G4y1y7z9
在这里插入图片描述

解法一：动态规划

class Solution {
    public int countSubstrings(String s) {
        // 1、dp[i][j]含义：字符串[i, j]是否为回文子串
        // 2、递归公式：dp[i][j]=dp[i+1][j-1];
        // 3、dp初始化：为了不影响递归中的判断，所有下标均初始化为false
        // 4、遍历顺序：当前状态是由左下角状态推导出来的，外层for倒序遍历，内层for正序遍历
        // 5、打印验证。
        boolean[][] dp = new boolean[s.length()][s.length()];
        int result=0;

        for(int i=s.length()-1;i>=0;i--){
            for(int j=i;j<s.length();j++){
                if(s.charAt(i)==s.charAt(j)){
                    if(j-i<=1){
                        dp[i][j]=true;
                        result++;
                    }else{
                        dp[i][j]=dp[i+1][j-1];
                        if(dp[i][j])result++;
                    }
                }
            }
        }
        return result;
    }
}

解法二：双指针中心扩散法

遍历数组，假定每个数组为中心元素，统计回文子串。
在遍历中心点的时候，要注意中心点有两种情况。一个元素可以作为中心点，两个元素也可以作为中心点。

class Solution {
    public int countSubstrings(String s) {
        int result=0;
        for(int i=0;i<s.length();i++){
            result+=extend(s, i, i);//一个元素作为中心点
            result+=extend(s, i, i+1);//两个元素作为中心点
        }
        return result;
    }
	// 中心扩散判断回文串
    public int extend(String s, int left, int right){
        int result = 0;
        while(left>=0 && right<s.length()){
            if(s.charAt(left)==s.charAt(right)){
                result++;
            }else{
                break;// 不相等就不能再构成回文串
            }
            left--;
            right++;
        }
        return result;
    }
}

516.最长回文子序列

教程视频：https://www.bilibili.com/video/BV1d8411K7W6
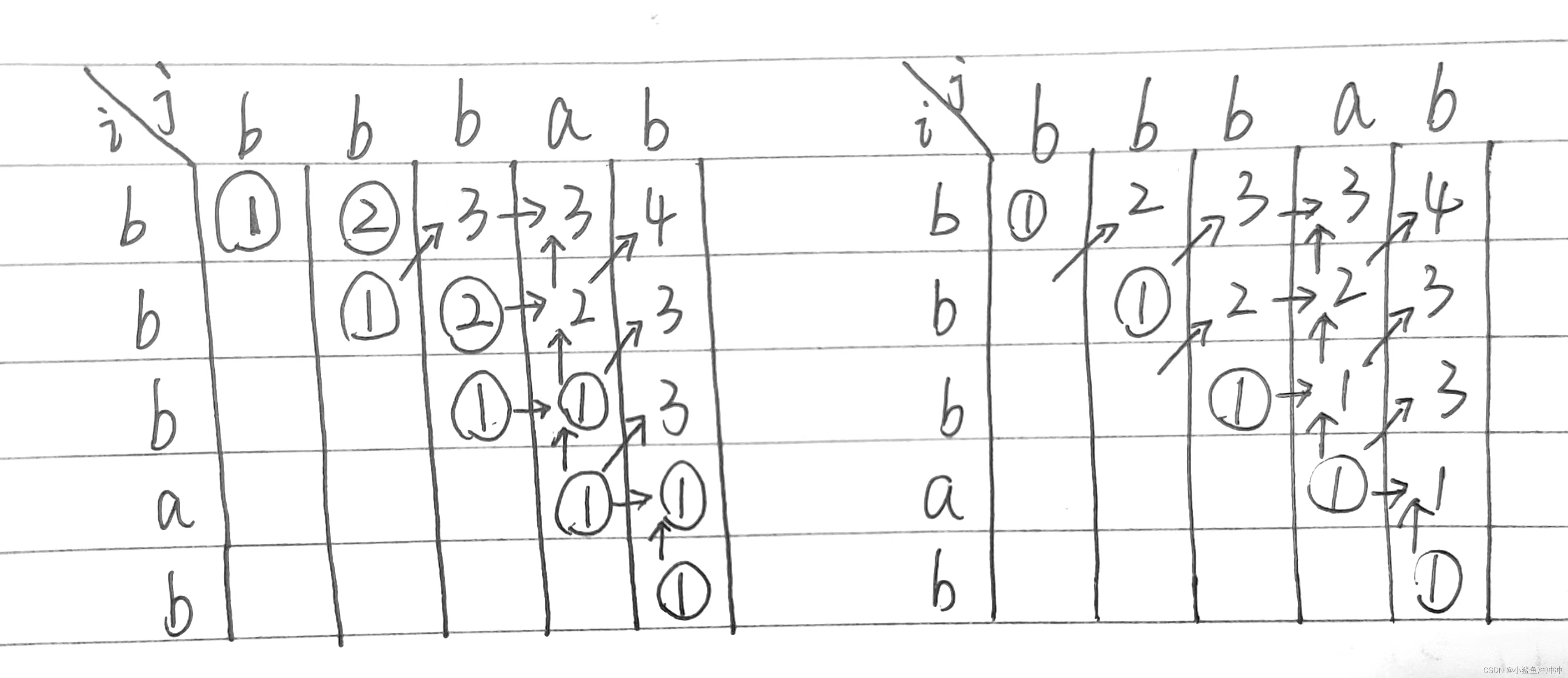
在这里插入图片描述

解法一：动态规划

在这里插入图片描述
右侧初始化一条对角线代码：(利用了数组默认值为0)

class Solution {
    public int longestPalindromeSubseq(String s) {
        // 1、dp[i][j]含义：字符串[i, j]中最长回文子串长度
        // 2、递归公式：从两侧向中间依次判断
        // 3、dp初始化：指向单个字符时，长度为1，dp[i][i]=1;
        // 4、遍历顺序：当前状态是由左下角状态推导出来的，外层for倒序遍历，内层for正序遍历
        // 5、打印验证。
        int[][] dp = new int[s.length()+1][s.length()+1];

        for(int i=s.length()-1;i>=0;i--){
            dp[i][i]=1;//初始化
            for(int j=i+1;j<s.length();j++){
                if(s.charAt(i)==s.charAt(j)){//外层两个字符相等
                    //累计回文子串长度
                    dp[i][j]=dp[i+1][j-1]+2;
                }else{//外层两个字符不相等
                    //比较删左侧和删右侧那个子串长度更长，取更长的值
                    dp[i][j]=Math.max(dp[i][j], Math.max(dp[i+1][j], dp[i][j-1]));
                }
            }
        }
        return dp[0][s.length()-1];
    }
}

左侧初始化两条对角线代码：

class Solution {
    public int longestPalindromeSubseq(String s) {
        // 1、dp[i][j]含义：字符串[i, j]中最长回文子串长度
        // 2、递归公式：从两侧向中间依次判断，两侧相等时dp[i][j]=dp[i+1][j-1]+2;，两侧不等时dp[i][j]=Math.max(dp[i+1][j], dp[i][j-1]);
        // 3、dp初始化：
        /* 
           if(s.charAt(i)==s.charAt(j)){
        	    if(j-i<=1){dp[i][j]=j-i+1;}
           }else{
           		dp[i][j]=Math.max(dp[i+1][j], dp[i][j-1]);
           }
       	*/
        // 4、遍历顺序：当前状态是由左下角状态推导出来的，外层for倒序遍历，内层for正序遍历
        // 5、打印验证。
        int[][] dp = new int[s.length()][s.length()];
        int result = 0;

        for(int i=s.length()-1;i>=0;i--){
            for(int j=i;j<s.length();j++){
                if(s.charAt(i)==s.charAt(j)){//外层两个字符相等
                    if(j-i<=1){//如果遍历到中心则直接赋值（初始化）
                        dp[i][j]=j-i+1;
                    }else{//否则累计回文子串长度
                        dp[i][j]=dp[i+1][j-1]+2;
                    }
                }else{//外层两个字符不相等
                    //比较删左侧和删右侧哪个子串长度更长，取更长的值（部分初始化）
                    dp[i][j]=Math.max(dp[i+1][j], dp[i][j-1]);
                }
                result=Math.max(dp[i][j],result);
            }
        }
        return result;
    }
}

动态规划总结篇

动规五部曲分别为：
1、dp数组（dp table）以及下标的含义
2、递推公式
3、dp数组初始化
4、遍历顺序
5、举例推导dp数组

动划基础

1 代码随想录算法训练营day38 | 动态规划理论基础，509. 斐波那契数，70. 爬楼梯，746. 使用最小花费爬楼梯

2 代码随想录算法训练营day39 | 62.不同路径，63. 不同路径 II

3 代码随想录算法训练营day41 | 343. 整数拆分，96.不同的二叉搜索树

背包问题系列

1 代码随想录算法训练营day42 | 01背包问题，你该了解这些！，01背包问题，你该了解这些！滚动数组， 416. 分割等和子集

2 代码随想录算法训练营day43 | 1049. 最后一块石头的重量 II ，494. 目标和，474.一和零，01背包问题总结

3 代码随想录算法训练营day44 | 完全背包，518. 零钱兑换 II，377. 组合总和 Ⅳ

4 代码随想录算法训练营day45 | 70. 爬楼梯（进阶），322. 零钱兑换，279.完全平方数

5 代码随想录算法训练营day46 | 139.单词拆分，多重背包，背包问题总结篇！

打家劫舍系列

代码随想录算法训练营day48 | 198.打家劫舍，213.打家劫舍II，337.打家劫舍III

股票系列

1 代码随想录算法训练营day49 | 121. 买卖股票的最佳时机，122.买卖股票的最佳时机II

2 代码随想录算法训练营day50 | 123.买卖股票的最佳时机III，188.买卖股票的最佳时机IV

3 代码随想录算法训练营day51 | 309. 最佳买卖股票时机含冷冻期，714.买卖股票的最佳时机含手续费，股票问题总结

子序列系列

1 代码随想录算法训练营day52 | 300.最长递增子序列，674. 最长连续递增序列，718. 最长重复子数组

2 代码随想录算法训练营day53 | 1143.最长公共子序列，1035.不相交的线，53. 最大子序和动态规划
3 代码随想录算法训练营day55 | 392.判断子序列，115.不同的子序列
4 代码随想录算法训练营day56 | 583. 两个字符串的删除操作，72. 编辑距离，编辑距离总结篇
5 代码随想录算法训练营day57 | 647. 回文子串，516.最长回文子序列，动态规划总结篇