叶值的最小代价生成树

力扣链接：1130. 叶值的最小代价生成树

题目描述

给你一个正整数数组 arr，考虑所有满足以下条件的二叉树：

每个节点都有 0 个或是 2 个子节点。
数组 arr 中的值与树的中序遍历中每个叶节点的值一一对应。
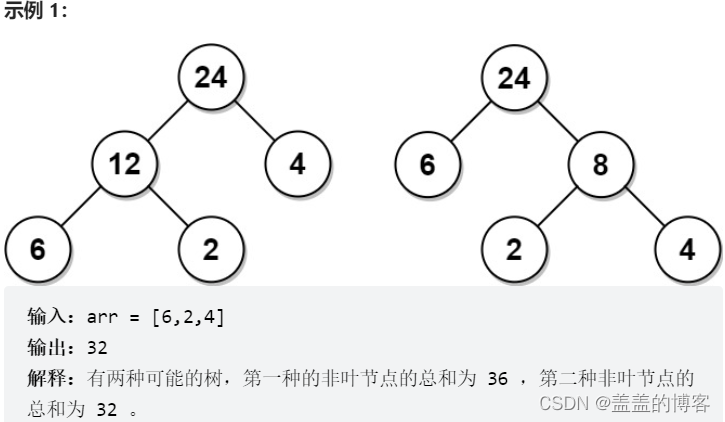
每个非叶节点的值等于其左子树和右子树中叶节点的最大值的乘积。
在所有这样的二叉树中，返回每个非叶节点的值的最小可能总和。这个和的值是一个 32 位整数。

如果一个节点有 0 个子节点，那么该节点为叶节点。

示例

Java代码1（单调栈）

class Solution {
    public int mctFromLeafValues(int[] arr) {
        Stack<Integer> stack = new Stack<>();
        stack.push(Integer.MAX_VALUE); //哨兵
        int res = 0;
        for(int i = 0; i < arr.length; i++) {
            while(stack.peek() < arr[i]) {
                res += stack.pop() * Math.min(arr[i], stack.peek());
            }
            stack.push(arr[i]);
        }
        while(stack.size() > 2) {
            res += stack.pop() * stack.peek();
        }
        return res;
    }
}

Java代码2（动态规划）

class Solution {
    public int mctFromLeafValues(int[] arr) {
        int len = arr.length;
        int[][] dp = new int[len][len];  
        int[][] maxVal = new int[len][len];
        
        for (int i = 0;i < len;i++)
            maxVal[i][i] = arr[i];
        for (int i = 0;i < len; i++){
            for (int j = i+1; j < len; j++){
                maxVal[i][j] = Math.max(maxVal[i][j-1],arr[j]);
                dp[i][j] = Integer.MAX_VALUE;
            }
        }
        
        for (int l = 1; l < len; l++){//l=j-i （长度）
            for (int i = 0; i < len-l; i++){//起始点i,终点i+l-1
                for (int k = i; k < i+l; k++){//中间分割点（根）
                    dp[i][i+l] = Math.min(dp[i][i+l],dp[i][k] + dp[k+1][i+l] + maxVal[i][k] * maxVal[k+1][i+l]);
                }
            }
        }
        return dp[0][len-1];
    }
}

---

来源：力扣（LeetCode）
链接：https://leetcode.cn/problems/minimum-cost-tree-from-leaf-values
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。