LeetCode - 10 正则表达式匹配

news2024/11/19 23:32:40

目录

题目来源

题目描述

示例

提示

题目解析

算法源码

题目来源

10. 正则表达式匹配 - 力扣（LeetCode）

题目描述

给你一个字符串 s 和一个字符规律 p，请你来实现一个支持 '.' 和 '*' 的正则表达式匹配。

'.' 匹配任意单个字符
'*' 匹配零个或多个前面的那一个元素
所谓匹配，是要涵盖 整个 字符串 s的，而不是部分字符串。

示例

示例 1

  • 输入：s = "aa", p = "a"
  • 输出：false
  • 解释："a" 无法匹配 "aa" 整个字符串。

示例 2

  • 输入：s = "aa", p = "a*"
  • 输出：true
  • 解释：因为 '*' 代表可以匹配零个或多个前面的那一个元素, 在这里前面的元素就是 'a'。因此，字符串 "aa" 可被视为 'a' 重复了一次。

示例 3

  • 输入：s = "ab", p = ".*"
  • 输出：true
  • 解释：".*" 表示可匹配零个或多个（'*'）任意字符（'.'）。

提示

  • 1 <= s.length <= 20
  • 1 <= p.length <= 20
  • s 只包含从 a-z 的小写字母。
  • p 只包含从 a-z 的小写字母，以及字符 . 和 *。
  • 保证每次出现字符 * 时，前面都匹配到有效的字符

题目解析

本题如果用正则表达式实现的话，逻辑非常简单，代码实现也非常简单，如下代码所示：

Java正则解法

import java.util.regex.Pattern;

class Solution {
    public boolean isMatch(String s, String reg) {
        return Pattern.compile("^" + reg + "$").matcher(s).find();
    }
}

  

JS正则解法

/**
 * @param {string} s
 * @param {string} p
 * @return {boolean}
 */
var isMatch = function(s, p) {
    return new RegExp(`^${p}$`).test(s);
};

Python正则解法

import re
class Solution(object):
    def isMatch(self, s, p):
        return re.compile("^"+ p +"$").match(s) is not None

但是，我们可以发现正则匹配的性能是非常差的，并且这题的目的是想让我们实现类似于正则匹配的功能，而不是让我们去套皮。

本题的最优解法是动态规划。

字符串s，正则p，现在想要确定正则p是否可以匹配字符串s。

我们假设 dp[ i ][ j ] 表示字符串s的0 ~ i部分，和正则p的0 ~ j 部分的匹配结果：

  • 要么是true，即匹配
  • 要么是false，即不匹配

那么此时，dp[ i ][ j ] 其实可以分情况讨论：

如果 p[ j ] == '*' 的话，

我们需要注意的是 '*' 在正则是一个量词符，用于表示它前面一个字符可能出现0次或多次。 

比如p = "abc*"，表示 '*' 前面的字符c可能出现0次或多次，即 p 可以匹配：

  • "ab"：c出现0次
  • "abc"：出现1次
  • "abcccccc"：c出现多次

那么我们不仅需要关注p[ j ]，还需要关注 p [ j - 1 ]，因为p[ j ]是量词符，而p[ j - 1 ]才是实际要匹配的内容字符。

比如上面例子p = "abc*"中，p[ j - 1 ] = 'c'，p[ j ] = '*'，而p[ j - 1 ] + p[ j ] 可以匹配字符串s最后部分的0个'c'，或者1个‘c’，或者多个'c'。

如果 p[ j - 1 ] != s[ i ] 的话，

那么p[ j - 1 ] + p[ j ] 就只能匹配 s 最后的0个字符，比如例子：p = "abc*"，s="ab"

如果 p[ j - 1 ] == s[ i ] 但是 p[ j - 1 ] != s[ i - 1 ]，

那么p[ j - 1 ] + p[ j ]就只能匹配 s 最后的1个字符，比如例子：p = "abc*"，s="abc"

如果 p[ j - 1 ] == s[ i ] 且 p[ j - 1 ] == s[ i - 1 ] 但是 p[ j - 1 ] != s[ i - 2 ]，

那么p[ j - 1 ] + p[ j ]就只能匹配 s 最后的2个字符，比如例子：p = "abc*"，s="abcc"

.............

如果 p[ j - 1 ] == s[ i ] 且 .... 且  p[ j - 1 ] == s[ i - k ] 但是 p [ j - 1 ] != s[ i - k - 1 ]

那么p[ j - 1 ] + p[ j ]就只能匹配 s 最后的k个字符

因此，基于上面逻辑写状态转义方程的话，有

if p[ j ] == '*'：

        dp[ i ][ j ] =

                     ( not_eq(p[ j - 1 ], s[ i ])   and  dp[ i ][ j - 2 ] )

                     or

                     ( eq(p[ j - 1 ], s[ i ])  and  not_eq(p[ j - 1 ], s[ i - 1 ])  and dp[ i - 1 ][ j - 2 ] )

                     or

                     ( eq(p[ j - 1 ], s[ i ])  and  eq(p[ j - 1 ], s[ i - 1 ])  and  not_eq(p[ j - 1 ], s[ i - 2 ]) and dp[ i - 2 ][ j - 2 ] )

                     or

                     ........

可以发现，这个状态转义方程是写不完的。因此需要简化，而dp[i][j]的简化，依赖于dp[i-1][j]，下面是dp[i-1][j]的状态转义方程

if p[ j ] == '*'：

        dp[ i - 1 ][ j ] =

                     ( not_eq(p[ j - 1 ], s[ i - 1 ])   and  dp[ i - 1 ][ j - 2 ] )

                     or

                     ( eq(p[ j - 1 ], s[ i -1 ])  and  not_eq(p[ j - 1 ], s[ i - 2 ])  and dp[ i - 2 ][ j - 2 ] )

                     or

                     ( eq(p[ j - 1 ], s[ i - 1 ])  and  eq(p[ j - 1 ], s[ i - 2 ])  and  not_eq(p[ j - 1 ], s[ i - 3 ]) and dp[ i - 3 ][ j - 2 ] )

                     or

                     ........

对比，dp[i][j] 和 dp[i-1][j]，可以发现，dp[i][j]的部分内容可以转化为dp[i-1][j]

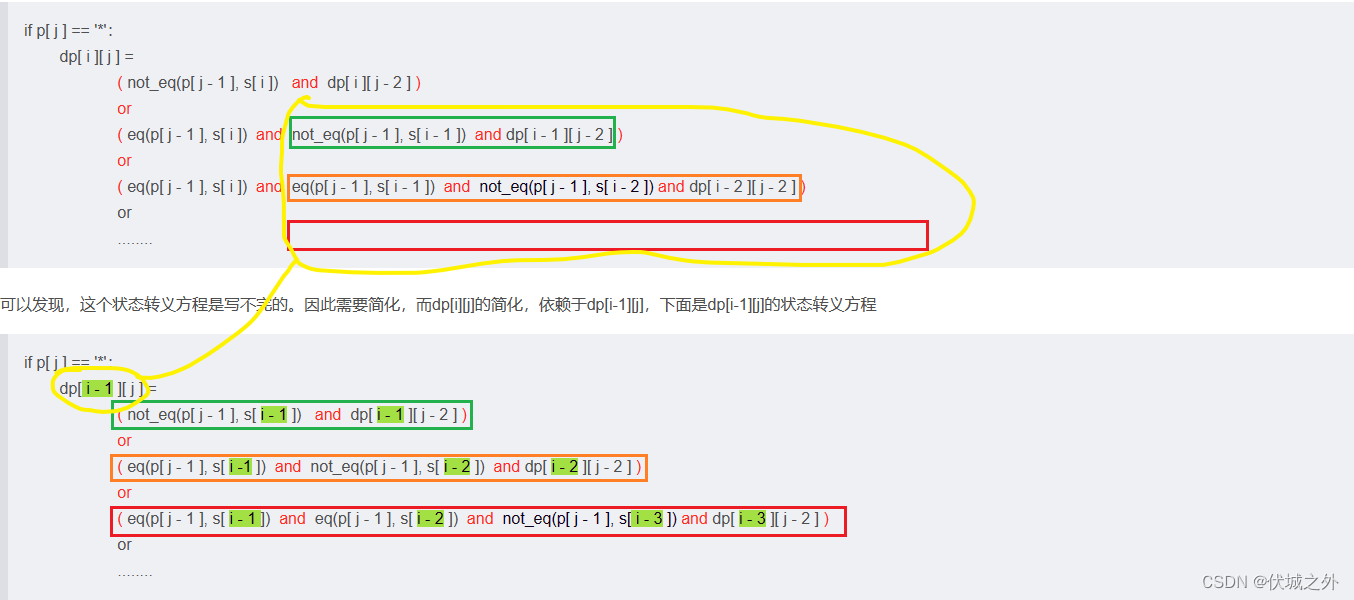
 即可得状态转义方程：

if p[ j ] == '*'：

        dp[ i ][ j ] = ( not_eq(p[ j - 1 ], s[ i ]) and dp[ i ][ j - 2 ] )  or  ( eq(p[ j - 1 ], s[ i ]) and dp[ i - 1 ][ j ] ) 

但是上面状态转义方程是存在问题的！！！！！

如果p[j] == '*'：

  1. 如果 p[j-1] != s[i]，那么 dp[i][j] 就可以分解为 dp[i][j-2]子问题，即正则p的j-1~j部分不匹配字符串s的任何内容，接下来只需要关心字符串s的0~i部分是否可以被正则p的0~j-2部分匹配。
  2. 如果 p[j-1] == s[i]，那么dp[i][j] 就可以分解为 dp[i-1][j] 子问题，因为 p[j-1] == s[i]，所以我们只需要关心字符串s的0~i-1部分是否可以被正则p的0~j匹配即可。

但是，实际上关于1，即使p[j-1] == s[i]的情况下，dp[i][j]也可以分解为dp[i][j-2]子问题，什么意思呢？

  1. 如果 p[j-1] == s[i]，那么正则p的j-1~j部分依旧可以选择不匹配字符串s的任何内容，接下来如果字符串s的0~i部分是否可以被正则p的0~j-2部分匹配，那么依然可以说明s可以被p匹配。

因此，最正确的状态转义方程是：

if p[ j ] == '*'：

        dp[ i ][ j ] = ( dp[ i ][ j - 2 ] )  or  ( eq(p[ j - 1 ], s[ i ]) and dp[ i - 1 ][ j ] ) 

另外关于，上面eq和not_eq该如何实现呢？

首先，如果 p[ j - 1 ] == s[ i ]的话，那么肯定是相同的，eq(p[ j - 1 ], s[ i ]) == true

其次，在正则表达式中，有一个通配符‘.’，它可以匹配任意一个实际字符，因此如果 p[ j - 1 ] == '.' 的话，则也可以认为 p[ j - 1 ] == s[ i ]，即eq(p[ j - 1 ], s[ i ]) == true

如果 p[ j ] ! = '*' 的话，

那么此时的判断就非常简单了，因为p[ j ]确定不是量词符了，因此p[ j ]就只能匹配一个字符s[ i ]

如果 eq(p[ j ], s[ i ])，那么 dp[i][j] = dp[i-1][j-1]，否则直接dp[i][j] = false

因此综合来看，dp[i][j]的状态转义方程如下：

if p[ j ] == '*'：
        dp[ i ][ j ] = ( not_eq(p[ j - 1 ], s[ i ]) and dp[ i ][ j - 2 ] )  or  ( eq(p[ j - 1 ], s[ i ]) and dp[ i - 1 ][ j ] ) 
else:
        dp[ i ][ j ] = eq(p[ j ], s[ i ]) ? dp[i - 1][j - 1] : false

当然，上面状态转义方程需要注意索引越界处理，必须要保证索引不越界。

关于，dp[i][j] 的初始化问题，比如dp[0][0]应该初始化为多少？

dp[0][0]的含义是 字符串s的0~0部分，是否可以被正则p的0~0部分匹配？

似乎说匹配也可以，不匹配也可以，因为正则为空。

因此，为了初始化容易理解，我们应该为s，p开头都加一个" "，即

s = " " + s

p = " " + p

那么其实原来dp[0][0]的问题，就变为dp[1][1]的问题，即字符串s的0~1部分，是否可以被正则p的0~1部分匹配，即" "是否可以被" "匹配，那么这里是肯定确定可以匹配的。

但是我们不能初始化dp[1][1] = true，而是需要初始化dp[0][0] = true。具体原因，大家可以基于上面状态转义方程，结合几个例子验证一下。

Java算法源码

class Solution {
  public boolean isMatch(String s, String p) {
    s = " " + s;
    p = " " + p;

    int n = s.length();
    int m = p.length();

    boolean[][] dp = new boolean[n][m];
    dp[0][0] = true;

    for (int i = 0; i < n; i++) {
      // 内层循环遍历的是正则p的范围，如果j=0.那么代表正则为空，此时匹配结果必然为false，而dp数组初始化时所有元素都初始化为了false，因此这里j可以从1开始
      for (int j = 1; j < m; j++) {
        if (p.charAt(j) == '*') {
          // 注意下面case1和case2仅为了方便理解，所以分开写了，实际时可以代入到case1 || case2中
          boolean case1 = j >= 2 && dp[i][j - 2];
          boolean case2 = eq(p.charAt(j - 1), s.charAt(i)) && i >= 1 && dp[i - 1][j];
          dp[i][j] = case1 || case2;
        } else {
          dp[i][j] = eq(p.charAt(j), s.charAt(i)) && i >= 1 && dp[i - 1][j - 1];
        }
      }
    }

    return dp[n - 1][m - 1];
  }

  public static boolean eq(char p, char s) {
    return p == s || p == '.';
  }
}

JS算法源码

/**
 * @param {string} s
 * @param {string} p
 * @return {boolean}
 */
var isMatch = function (s, p) {
  s = " " + s;
  p = " " + p;

  const n = s.length;
  const m = p.length;

  const dp = new Array(n).fill(0).map(() => new Array(m).fill(false));
  dp[0][0] = true;

  for (let i = 0; i < n; i++) {
    // 内层循环遍历的是正则p的范围，如果j=0.那么代表正则为空，此时匹配结果必然为false，而dp数组初始化时所有元素都初始化为了false，因此这里j可以从1开始
    for (let j = 1; j < m; j++) {
      if (p[j] == "*") {
        // 注意下面case1和case2仅为了方便理解，所以分开写了，实际时可以代入到case1 || case2中
        const case1 = j >= 2 && dp[i][j - 2];
        const case2 = eq(p[j - 1], s[i]) && i >= 1 && dp[i - 1][j];
        dp[i][j] = case1 || case2;
      } else {
        dp[i][j] = eq(p[j], s[i]) && i >= 1 && dp[i - 1][j - 1];
      }
    }
  }

  return dp[n - 1][m - 1];
};

function eq(p, s) {
  return p == s || p == ".";
}

Python算法源码

class Solution(object):
    def isMatch(self, s, p):
        s = " " + s
        p = " " + p

        n = len(s)
        m = len(p)

        dp = [[False] * m for _ in range(n)]
        dp[0][0] = True

        for i in range(n):
            # 内层循环遍历的是正则p的范围，如果j=0.那么代表正则为空，此时匹配结果必然为false，而dp数组初始化时所有元素都初始化为了false，因此这里j可以从1开始
            for j in range(1, m):
                if p[j] == '*':
                    # 注意下面case1和case2仅为了方便理解，所以分开写了，实际时可以代入到case1 || case2中
                    case1 = j >= 2 and dp[i][j - 2]
                    case2 = self.eq(p[j - 1], s[i]) and i >= 1 and dp[i - 1][j]
                    dp[i][j] = case1 or case2
                else:
                    dp[i][j] = self.eq(p[j], s[i]) and i >= 1 and dp[i - 1][j - 1]

        return dp[n - 1][m - 1]

    def eq(self, p, s):
        return p == s or p == '.'

  

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/591473.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

SpringBoot框架理解

SpringBoot框架理解

1 SpringBoot入门 1.2 什么是SpringBoot 1 官网的解释 ​ Spring在官方首页是这么说的&#xff1a;说使用SpringBoot可以构造任何东西&#xff0c;SpringBoot是构造所有基于Spring的应用程序的起点,SpringBoot在于通过最少的配置为你启动程序。 2 我的理解 SpringBoot是Sp…
阅读更多...
损失函数——交叉熵损失（Cross-entropy loss）

损失函数——交叉熵损失（Cross-entropy loss）

交叉熵损失&#xff08;Cross-entropy loss&#xff09;是深度学习中常用的一种损失函数&#xff0c;通常用于分类问题。它衡量了模型预测结果与实际结果之间的差距&#xff0c;是优化模型参数的关键指标之一。以下是交叉熵损失的详细介绍。 假设我们有一个分类问题&#xff0…
阅读更多...
基于深度学习的高精度山羊检测识别系统（PyTorch+Pyside6+YOLOv5模型）

基于深度学习的高精度山羊检测识别系统（PyTorch+Pyside6+YOLOv5模型）

摘要&#xff1a;基于深度学习的高精度山羊检测识别系统可用于日常生活中或野外来检测与定位山羊目标&#xff0c;利用深度学习算法可实现图片、视频、摄像头等方式的山羊目标检测识别&#xff0c;另外支持结果可视化与图片或视频检测结果的导出。本系统采用YOLOv5目标检测模型…
阅读更多...
elementUI中＜el-select＞下拉框选项过多的页面优化方案——多列选择

elementUI中＜el-select＞下拉框选项过多的页面优化方案——多列选择

效果展示(多列可以配置) 一、icon下拉框的多列选择&#xff1a; 二、常规、通用下拉框的多列选择&#xff1a; 【注】第二种常规、通用下拉框的多列选择&#xff0c;是在第一种的前端代码上删除几行代码就行&#xff08;把icon显示标签删去&#xff09;&#xff0c;所以下面着重…
阅读更多...
陕西省养老服务人才培训基地申报条件范围、认定材料流程

陕西省养老服务人才培训基地申报条件范围、认定材料流程

今天为大家整理了陕西省养老服务人才培训基地申报条件范围、奖励措施等内容&#xff0c;感兴趣的朋友们可以了解一下&#xff01; 如果想要申报西安市、宝鸡市、铜川市、咸阳市、渭南市、延安市、汉中市、榆林市、安康市、商洛市的项目政策&#xff0c;详情见下图 目标任务 陕…
阅读更多...
Games104现代游戏引擎学习笔记11

Games104现代游戏引擎学习笔记11

胶囊&#xff1a;两层。 内层&#xff1a;真正碰撞的层级 外层&#xff1a;类似保护膜&#xff0c;防止离别的东西太近&#xff0c;高速移动时卡进物体。另一个作用是防止过于贴近摄像机的进平面&#xff0c;看到墙背后的物体 朝墙移动时&#xff0c;实际往往并不是撞击&#…
阅读更多...
Java程序设计入门教程-- switch选择语句

Java程序设计入门教程-- switch选择语句

switch选择语句 情形 虽然if…else语句通过嵌套可以处理多分支的情况&#xff0c;但分支不宜太多&#xff0c;在Java语言中&#xff0c;提供了switch语句可以直接、高效地处理多分支选择的情况。 格式 switch &#xff08;表达式&#xff09; { case 常量表达式1&#x…
阅读更多...
EclipseCDT远程交叉编译远程单步调试基于makefile例程（实测有效）

EclipseCDT远程交叉编译远程单步调试基于makefile例程（实测有效）

文章目录 前言&#xff1a;1. 新建工程2. 远程编译环境配置2.1 下载sshfs并挂载目录2.2 Debug配置2.3安装EclipseCDT的远程插件2.4 拷贝gdbserver 3. 调试总结: 前言&#xff1a; 之前写过一篇VSCode远程调试linux&#xff0c;当时是把程序以及代码通过远程的方式&#xff0c;…
阅读更多...
pycharm内置Git操作失败的原因

pycharm内置Git操作失败的原因

文章目录 问题简介解决方案DNS缓存机制知识的自我理解 问题简介 最近在pycharm中进行代码改动递交的时候&#xff0c;总是出现了连接超时或者推送被rejected的情况&#xff0c;本以为是开了代理导致的&#xff0c;但是关闭后还是推送失败&#xff0c;于是上网查了以后&#xf…
阅读更多...
查看MySQL服务器是否启用了SSL连接，并且查看ssl证书是否存在

查看MySQL服务器是否启用了SSL连接，并且查看ssl证书是否存在

文章目录 一、查看MySQL服务器是否启用了SSL连接 1.登录MySQL服务器 2.查看SSL配置 二、查看证书是否存在 前言 查看MySQL服务器是否启用了SSL连接&#xff0c;并且查看ssl证书是否存在 一、查看MySQL服务器是否启用了SSL连接 1.登录MySQL服务器 在Linux终端中&#xf…
阅读更多...
【Windows驱动篇】解决Windows驱动更新导致AMD Software软件无法正常启动问题

【Windows驱动篇】解决Windows驱动更新导致AMD Software软件无法正常启动问题

【Windows驱动篇】解决Windows驱动更新导致AMD Software软件无法正常启动问题 【操作前先备份好电脑数据&#xff01;&#xff01;&#xff01;设置系统还原点等&#xff0c;防止系统出现问题&#xff01;&#xff01;&#xff01;谨慎请操作&#xff01;】 【操作前先备份好…
阅读更多...
Windows本地提权 · 上篇

Windows本地提权 · 上篇

目录 at 命令提权 sc 命令提权 ps 命令提权 利用的是windows的特性&#xff0c;权限继承&#xff0c;命令或者服务创建调用的时候会以system权限调用&#xff0c;那么这个命令或者服务的权限也是system。 进程迁移注入提权 pinjector进程注入 MSF进程注入 令牌窃取提权…
阅读更多...
chatgpt赋能python：Python中日期转换：从字符串到日期对象

chatgpt赋能python：Python中日期转换：从字符串到日期对象

Python中日期转换&#xff1a;从字符串到日期对象 作为一个经验丰富的Python工程师&#xff0c;日期转换在我的日常编码工作中经常遇到。Python提供了一些内置函数和模块&#xff0c;可以将字符串转换为日期对象或将日期对象格式化为特定的字符串。本篇文章将带您深入了解Pyth…
阅读更多...
chatgpt赋能python：Python中的并运算：介绍及应用

chatgpt赋能python：Python中的并运算：介绍及应用

Python中的并运算&#xff1a;介绍及应用 Python是一种功能强大且易于使用的编程语言&#xff0c;它的灵活性使得我们可以应用各种算法和数据结构进行处理。其中&#xff0c;位运算是Python中非常棒的特性之一&#xff0c;而其中又有一个重要的运算符——并运算。 什么是并运…
阅读更多...
chatgpt赋能python：Python中的或运算：学习这个重要概念

chatgpt赋能python：Python中的或运算：学习这个重要概念

Python中的或运算&#xff1a;学习这个重要概念 或运算是Python编程语言中一个重要的概念。了解如何使用或运算可以帮助程序员编写更有效和有意义的代码。在此文章中&#xff0c;我们将介绍Python中或运算的基础知识以及如何使用它来编写各种类型的代码。 什么是或运算&#…
阅读更多...
Android笔记--内存管理

Android笔记--内存管理

内存(Memory)是计算机的重要部件&#xff0c;也称主存储器&#xff0c;它用于暂时存放CPU中的运算数据&#xff0c;以及与硬盘等外部存储器交换的数据。Android中&#xff0c;内存是如何分配的&#xff1f;当启动一个android程序时&#xff0c;会启动一个dalvik vm进程&#xf…
阅读更多...
linux条件变量知识点总结

linux条件变量知识点总结

与条件变量相关API 条件变量是线程另一可用的同步机制。条件变量给多个线程提供了一个会合的场所。条件变量与互斥量一起使用时&#xff0c;允许线程以无竞争的方式等待特定的条件发生。 条件本身是由互斥量保护的。线程在改变条件状态前必须首先锁住互斥量&#xff0c;其他线程…
阅读更多...
chatgpt赋能python：Python中的“5“+“5“:了解运算符重载和字符串拼接

chatgpt赋能python：Python中的“5“+“5“:了解运算符重载和字符串拼接

Python中的 “5”“5”: 了解运算符重载和字符串拼接 Python中的运算符重载允许我们自定义类型的操作符行为。当我们使用加号运算符将两个对象相加时&#xff0c;Python会动态地确定该使用哪种类型的操作符行为。在使用字符串时&#xff0c;加号可以用于字符串的连接&#xff…
阅读更多...
【编译、链接、装载二】/lib/ld64.so.1: bad ELF interpreter: 没有那个文件或目录

【编译、链接、装载二】/lib/ld64.so.1: bad ELF interpreter: 没有那个文件或目录

【编译和链接二】bash: ./test.out: /lib/ld64.so.1: bad ELF interpreter: 没有那个文件或目录 一、问题起因二、ldd查看三、解决方案一&#xff1a;使用gcc链接四、查找其他解决方案五、解决方案二&#xff1a;软链接 bash: ./test.out: /lib/ld64.so.1: bad ELF interpreter…
阅读更多...
SpringBoot框架总结

SpringBoot框架总结

一、SpringBoot框架的概念 1、传统框架的弊端 例如传统的SSM框架整合了MyBatis、Spring、SpringMVC框架&#xff0c;但其需要繁琐且重复的配置使程序员很是痛苦 2、SpringBoot框架 SpringBoot框架在传统框架的基础上对其进一步封装&#xff0c;只需要一些简单的配置&#x…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023