梯度下降法有两个比较大的缺点：

--计算花时间

--容易陷入局部最优解

比如以下形状的函数，最优解取决于初始值的选取。

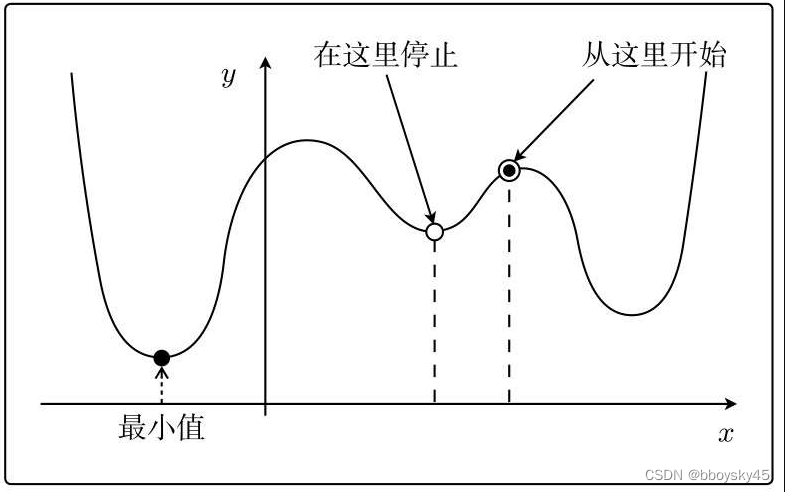
梯度下降法的表达式如下，这个表达式使用了所有训练数据的误差：

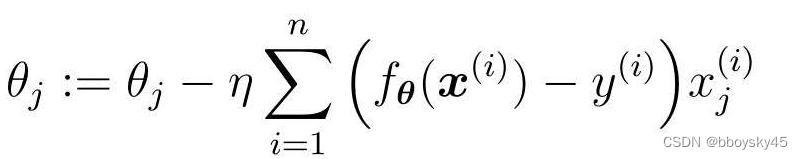
随机梯度下降法表达式：

在随机梯度下降法中会随机选择一个训练数据，并使用它来更新参数。这个表达式中的k就是被随机选中的数据索引。

梯度下降法更新1次参数的时间，随机梯度下降法可以更新n次。此外，随机梯度下降法由于训练数据是随机选择的，更新参数时使用的又是选择数据时的梯度，所以不容易陷入目标函数的局部最优解。

小批量（mini-batch）梯度下降法

当然，可以随机选择1个训练数据的做法，也肯定有随机选择m个训练数据来更新参数的做法。

设随机选择m个训练数据的索引的集合为K,

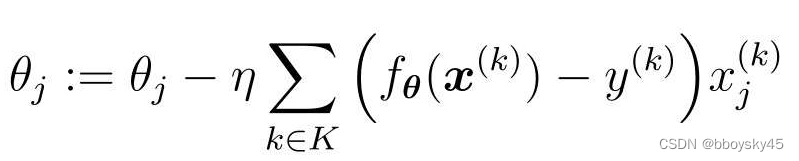
这种做法被称为小批量（mini-batch）梯度下降法。

这是介于最速下降法和随机梯度下降法之间的方法，不管是随机梯度下降法还是小批量梯度下降法，我们都必须考虑学习率η。把η设置为合适的值是最重要的。