一、机械臂运动学
机械臂运动学就是根据未端执行器与所选参考坐标系之间的几何关系,确定末端执行器的空间位置和姿态与各关节变量之间的数学关系。包括正运动学 (Forward Kinematics)和逆运动学 (InverseKinematics)两部分。
正运动学就是根据给定的机器人的各个关节变量,计算未端执行器的位置和姿态,也被称为机器人运动学建模。
逆运动学则是根据已知的末端执行器的位置和姿态,计算机器人各个关节变量,也被称为机器人运动学求解。
关节变量->机械臂末端执行器的姿势=正向运动学
机械臂未端执行器的位姿->关节变量=逆向运动学
二、正运动学D-H建模
1.标准型D-H法
(1)坐标系建在连杆的输出端,适合应用于开链结构的机器人
(2)树形结构与闭链结构的机器人,连杆坐标系会产生歧义
2.改进型D-H法
(1)坐标系建在连杆的输入端
(2)对开链、树状、闭链结构的机器人都适用
基本步骤
1.确定关节、连杆的描述:确定关节、连杆的描述及其尺寸
2.建立DH坐标系
规则:
(1)z轴是旋转关节的旋转轴
(2)x轴必须垂直于当前z轴
(3)x轴必须与前一个z轴垂直(规则不适用于第0关节)x2垂直于z1,x6可以做延长线和前一个z轴z5垂直
(4)y轴由x轴和z轴通过使用右手坐标系确定
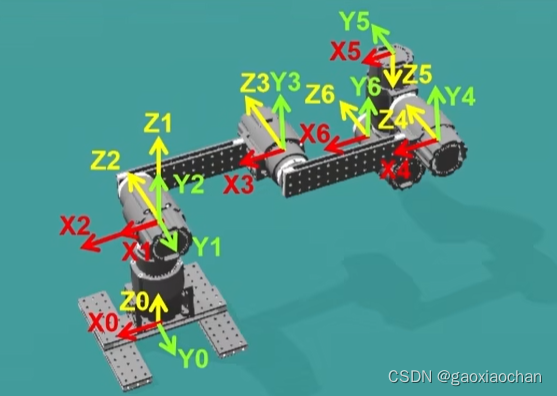
3.确定DH参数(di、θi、ai、αi)
di为沿Zi-1 轴从Xi到的距离,与Zi-1方向相同为正;
θi为绕Zi-1 轴从Xi到的转角,绕Zi-1正向转动方向为正;
ai为沿Xi轴从Zi到Zi+1的距离,与Xi方向相同为正;
αi为绕Xi轴从Zi-1到Zi的转角,绕Xi正向转动方向为正。
4.计算正向运动学:标准D-H参数,相邻坐标系的变换矩阵
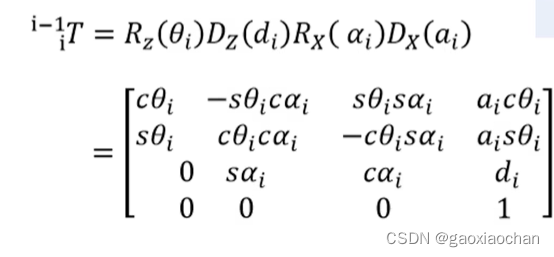
T01 = DHTransform(pi/2 , 0 , d1 , theta[0])
T12 = DHTransform(0,-a2, 0 , theta[1])
T23 = DHTransform(0,-a3, 0 , theta[2])
T34 = DHTransform(pi/2,0,d4, theta[3])
T45 = DHTransform(-pi/2,d5,theta[4])
T56 = DHTransform(0,0,d6,theta[5])
T06 = T01*T12*T23*T34*T45*T56
matrixs[0,0] = cth
matrixs[1,0] = sth
matrixs[0,1] = -sth * ca
matrixs[1,1] = cth * ca
matrixs[2,1] = sa
matrixs[0,2] = sth * sa
matrixs[1,2] = -cth *sa
matrixs[2,2] = ca
matrixs[0,3] = a*cth
matrixs[1,3] = a*sth
matrixs[2,3] = d
matrixs[3,3] = 1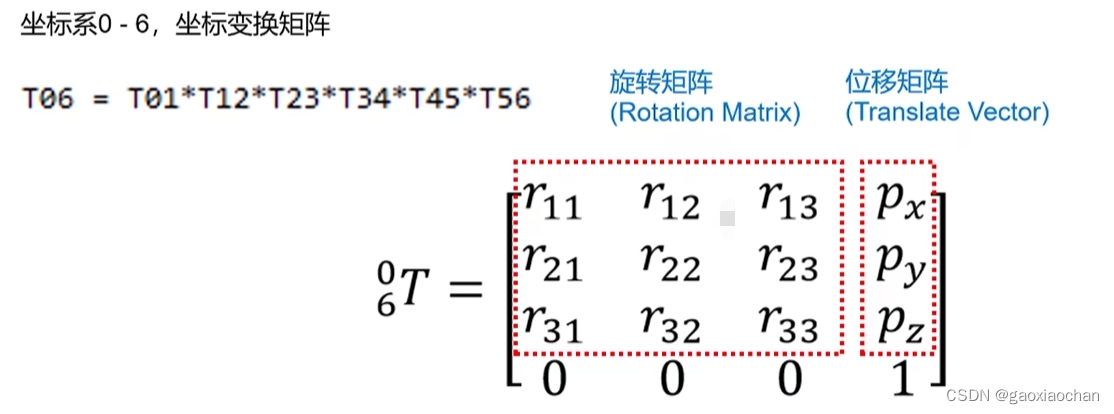
三、逆向运动学
逆运动学:是根据已知的末端执行器的位置和姿态,计算机器人各个关节变量,也被称为机器人运动学求解。
1.解析解法
(1)代数法
(2)几何法
2.数值解法
(1)迭代法
(2)优化法
解算思路:
初始坐标系:
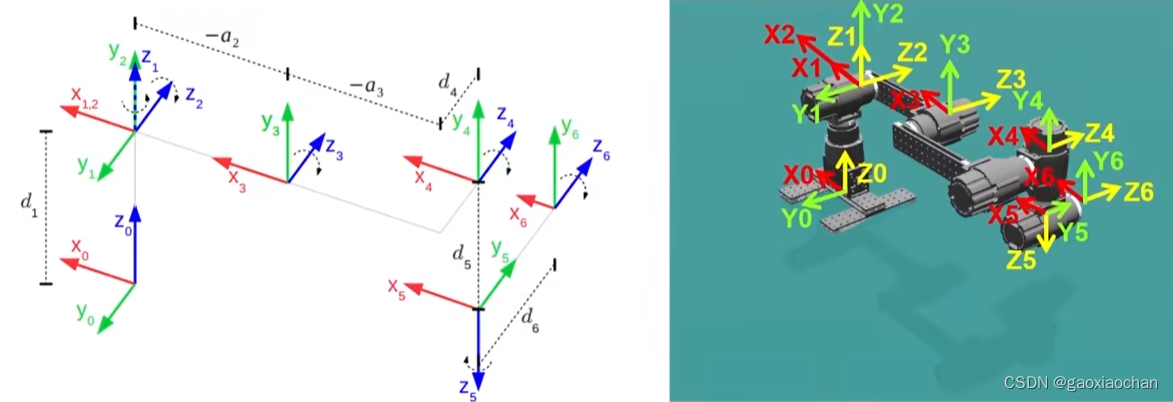
解算顺序:(方便进行解算,已知末端位置的状态θ1,θ5、θ6也能计算出来)
1.计算θ1
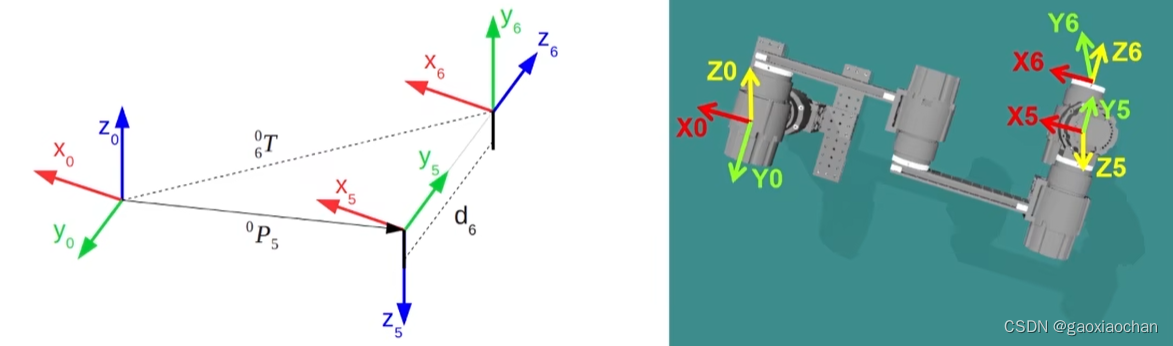
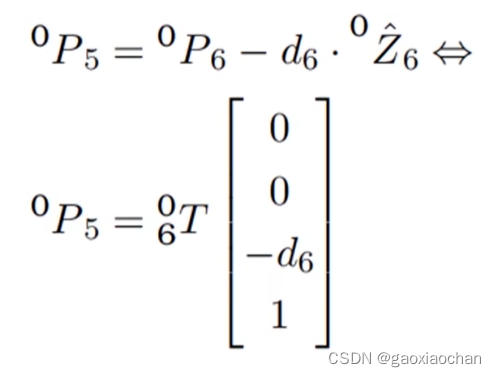


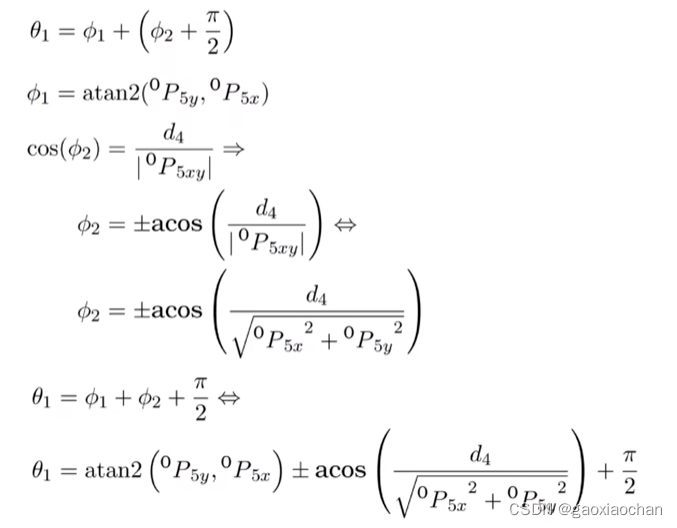
2.计算θ5
(1)转动θ5后的关节坐标系
(2)将机械臂简化
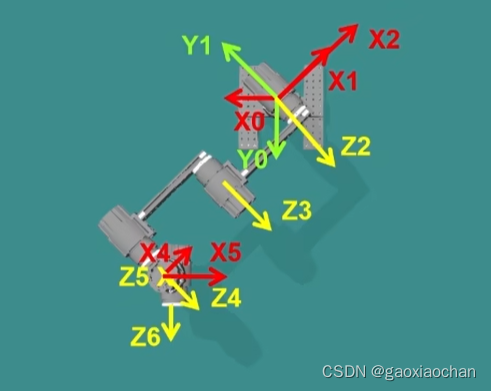
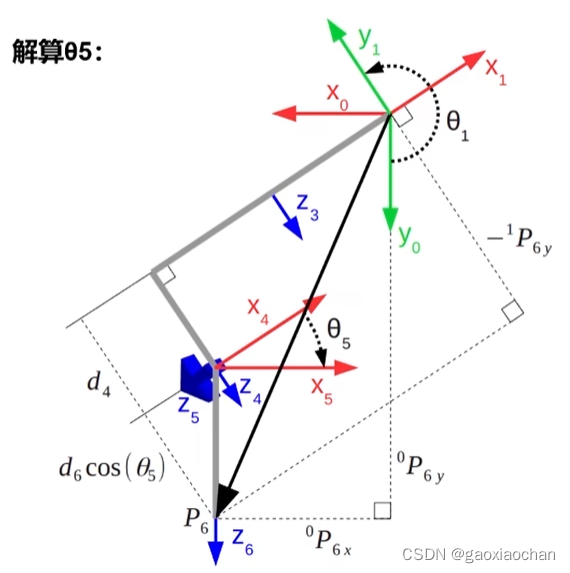

3.计算θ6
(1)机械臂初始的关节坐标系
(2)将机械臂简化,并确定θ6方向
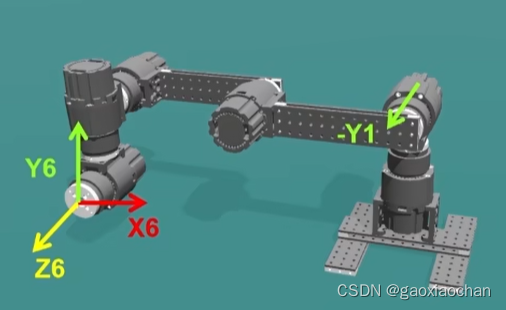
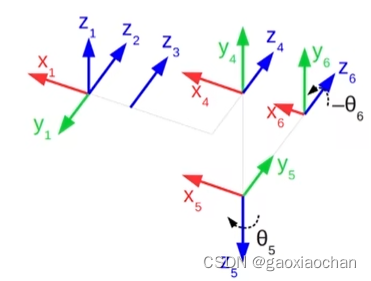
(1)将关节6转动-θ6
(2)将末端抽象为球坐标系
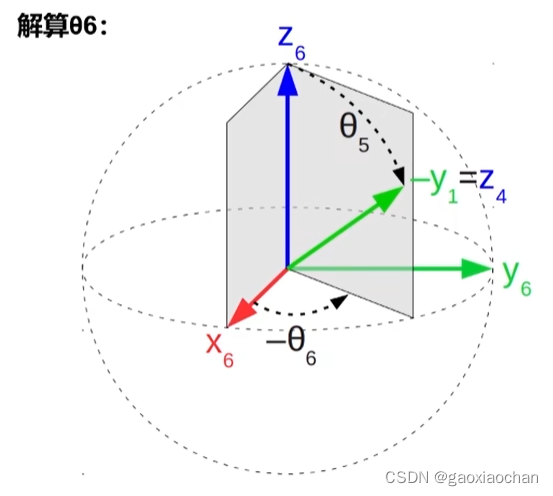

4.计算θ3
(1)将关节2转动θ2
(2)将关节3转动-θ3
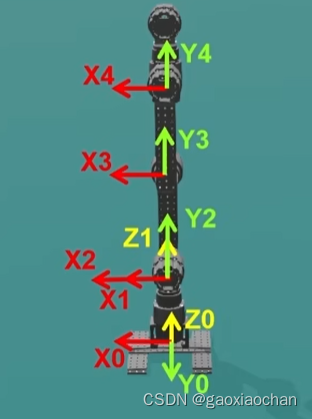
(1)将机械臂简化,并注意初始位置
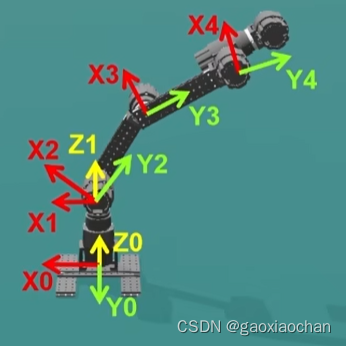
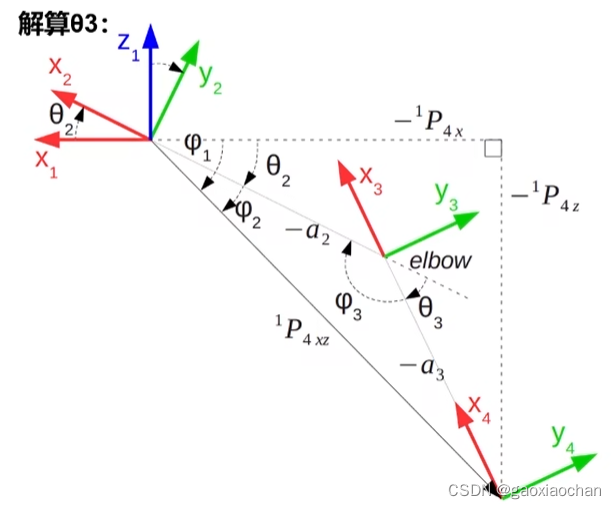
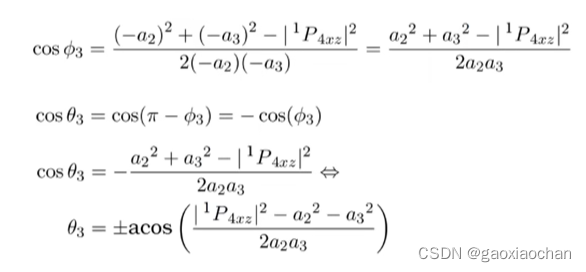
5.计算θ2

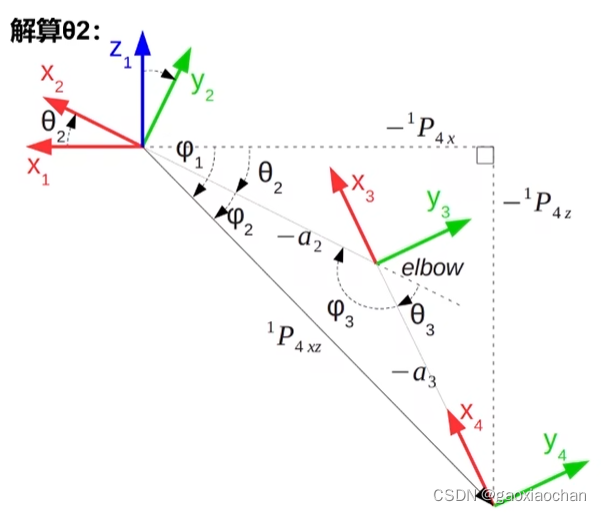
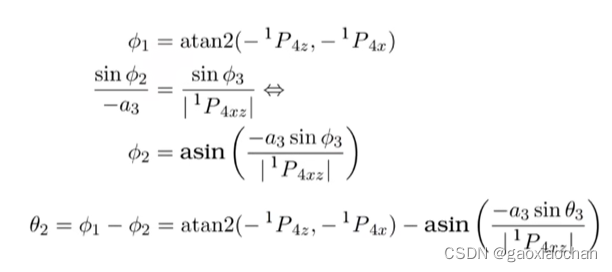
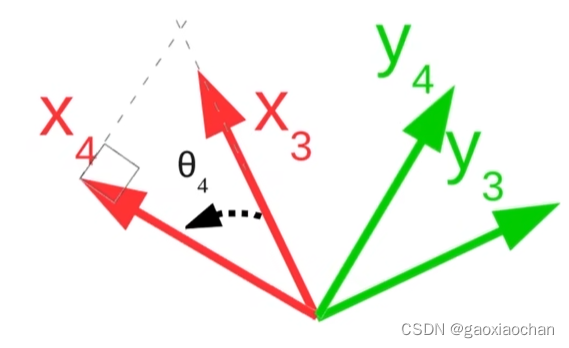
6.计算θ4

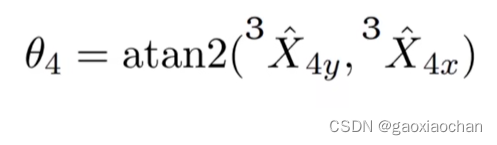
![[java]关于会话Session](https://img-blog.csdnimg.cn/7473bf535abf4a39ae175154f049b46a.png)