2021年长三角高校数学建模竞赛

B题锅炉水冷壁温度曲线

原题再现：

在燃煤发电过程中，锅炉是一种重要的热能动力设备。它通过在炉膛中燃烧煤粉释放热量，将水加热成一定温度（或压力）的蒸汽，蒸汽再推动汽轮机旋转并驱动发电机发电。锅炉的主要受热部分是水冷壁，通常由数排钢管组成，分布于锅炉炉膛的四周，其内部为流动的水，用于吸收炉膛中高温燃烧产生的辐射热量，水受热蒸发产生高压蒸汽。水冷壁的结构如图 1 所示。本题旨在通过数学模型对水冷壁温度曲线进行分析。
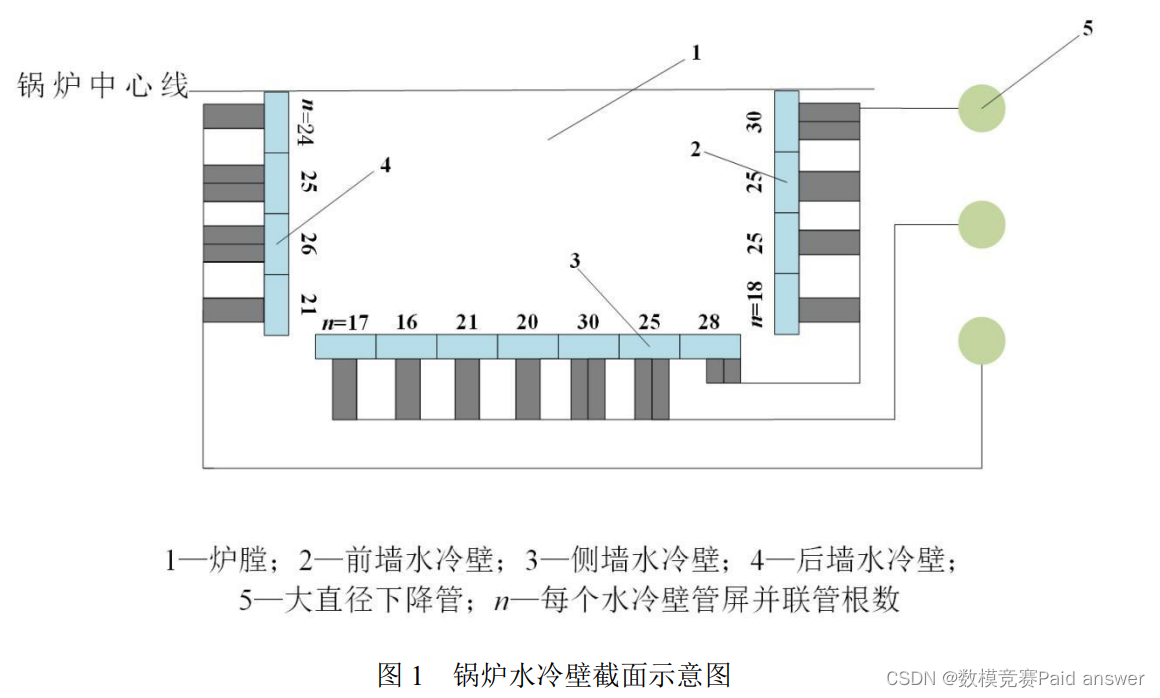
在这里插入图片描述
在实际生产过程中，希望水冷壁的温度变化尽可能平稳，同时为保证安全，水冷壁温度不宜过高，否则有烧坏的风险。按照实际经验，操作人员给出的水冷壁温度超温报警线为 445℃。影响水冷壁温度的因素有很多，包括锅炉负荷、蒸汽温度、蒸汽压力、燃料量、水煤比等。本题中给出了 10 个具有代表性水冷壁管道的温度值，采样频率为 15s，共 5000 组数据，具体见附件 1；同时给出了影响水冷壁温度的 153 个输入变量的 5000 组数据，其中包括 111 个操作变量和 42个状态变量（注 1），具体见附件 2。请利用这些信息和数据，建立数学模型解决以下问题。
1. 统计分析各个水冷壁管道的温度数据，并给出刻画这些温度时间序列数据变化情况的特征。
2. 请对附件 1 中 10 个水冷壁管道的温度数据曲线进行评价，确定其中的最优工作曲线和最差工作曲线。
3. 请利用附件 1 和附件 2 中的数据，分别建立 10 个水冷壁管道温度变化规律的数学模型，并对模型效果进行评价。
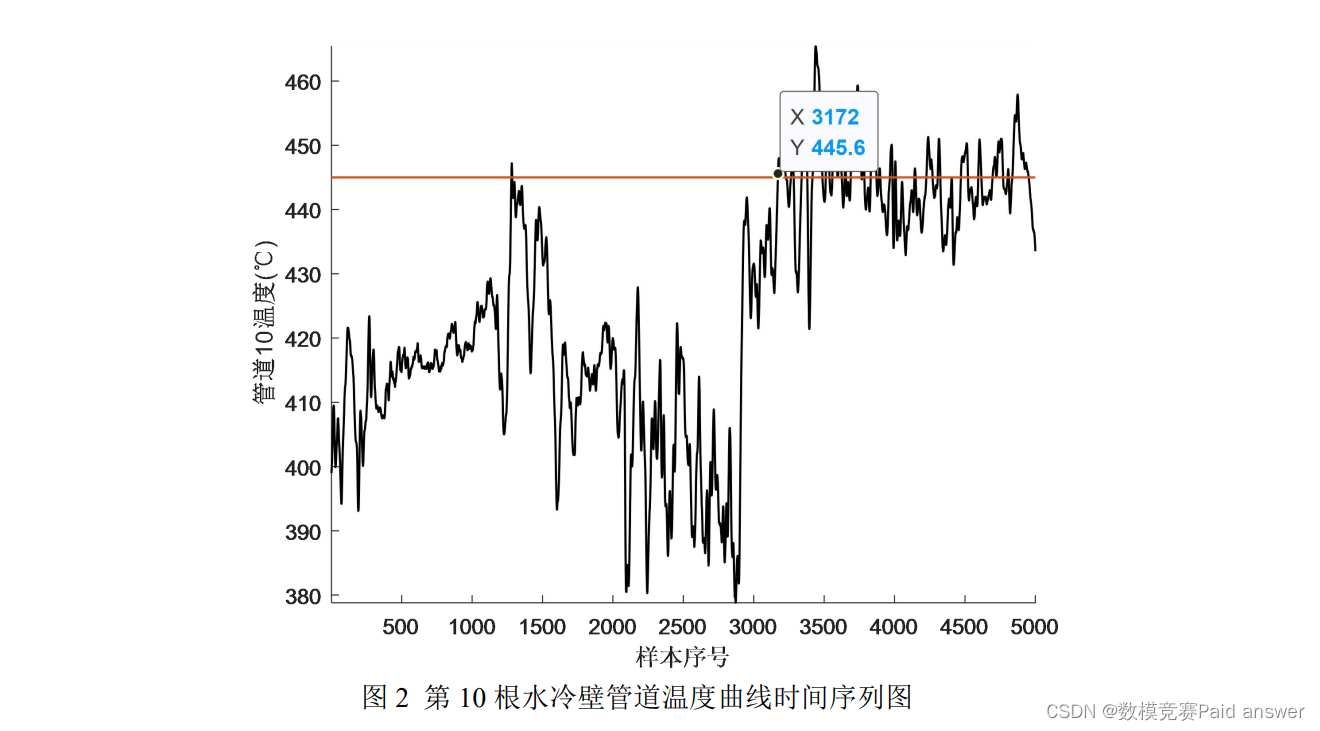
4. 第 10 个水冷壁管道温度曲线如图 2 所示，从图中可以看出，在第 3172 个样本点后水冷壁出现明显的超温现象，请基于给出的数据，分析并定位引发超温现象的主要操作变量。
5. 请针对第 10 个水冷壁管道温度曲线超温段建立优化模型，给出该超温段从第3172 个样本开始的最优调节策略，满足操控的变量数尽量少、操作变量的调控量尽量小、优化调节后的工作曲线与问题 2 中的最优工作曲线的特征尽量吻合。

在这里插入图片描述
注 1：
这里的操作变量，也常称作控制变量，是指在锅炉燃烧过程中，操作人员能够根据实际生产的需要而进行调节的量；而状态变量是用来描述锅炉燃烧系统运行状态的量，它的取值由相关检测设备采集得到，操作人员无法进行直接调节。

整体求解过程概述(摘要)

锅炉水冷壁本质上是一个热交换过程。当水冷壁出现超温现象时，可能会造成管壁过热损坏，需要对水冷壁温度进行调控。所以，研究操作变量与水冷壁温度的关系，对找出有效的调控策略具有重要意义。本文通过数据挖掘技术建立了基于 XGBoost-BP 的锅炉水冷壁温度预测模型，并给出了管道 10 出现超温现象后的最优调整策略。
对于问题一，统计分析各个水冷壁管道的温度数据，并给出刻画这些温度时间序列数据变化情况的特征。首先，通过分析附件一中的样本数据，通过循环遍历法验证了附件一数据的完整性。其次，对各个水冷壁管道的温度进行排序，然后计算得到每个水冷壁管道温度均值、众数、中位数等。最后，绘制了各个水冷壁管道的温度时间序列曲线，观察曲线，发现在前 2500 组数据中，曲线呈先上升后下降的变化趋势，后 2500 组数据趋于平稳的特征。
对于问题二，对附件一中 10 个水冷壁管道的温度数据曲线进行评价，确定其中的最优工作曲线和最差工作曲线。首先，以 445℃为标志对温度数据曲线进行粗评价：管道 1～8 为较好曲线，管道 9～10 为较差曲线。其次，使用递归法计算得到每个水冷壁管道的温度区间：管道 3 温度区间为 56℃，管道 10 温度区间为 86.6℃。然后，利用方差进行稳定性分析，得到管道 3 的方差最小，值为 113.98，管道 10 的方差最大，值为349.47。最终，确定管道 3 温度曲线为最优工作曲线，管道 10 工作曲线为最差工作曲线。
对于问题三，请利用附件 1 和附件 2 中的数据，分别建立 10 个水冷壁管道温度变化规律的数学模型，并对模型效果进行评价。首先，使用四分位法检测特征变量数据的异常值并剔除异常值。其次，使用 K 最近邻法，填充少量缺失的特征变量的数据。然后，通过方差分析、XGBoost 特征重要性得分、Spearman 相关性分析等方法对特征变量进行筛选，选出 24 个特征变量。最终，建立 XGBoost-BP 神经网络模型、随机森林、支持向量机回归模型对水冷壁管道温度进行预测，得出 XGBoost-BP 神经网络的预测效果最好，并通过 RMSE、MAE、R2 评估指标，证明了本文所创建的 XGBoost-BP 神经网络模型的有效性。
对于问题四，针对管道 10 出现的超温现象，分析并定位引发超温现象的主要操作变量。首先，利用 XGBoost 计算了各个操作变量在[3000,3300]区间和[3100,3200]区间中的特征重要性得分并排序。其次，对各操作变量与温度时间序列的相关性进行分析。提取 12 个主要操作变量。然后，调整上述操作变量，计算调整前后温度变化量。最终，获得影响管道 10 出现超温现象的 9 个主要操作变量。
对于问题五，针对第 10 个水冷壁管道温度曲线超温段建立优化模型，给出该超温段从第 3172 个样本开始的最优调节策略。首先，本文利用问题三构建的管道 10 模型作为管道温度预测模型，通过附件二确定各操作变量的取值范围作为约束条件，寻找管道10 温度下降的主要操作变量。其次，利用差分进化算法随机搜索管道 10 与最优温度曲线的最小差值，经过统计分析，我们确定了需要调节的 25 个变量和它们各自的调节量。

模型假设：

1、当两个变量特征变化趋势相似时，认为它们包含的信息也相似；
2、不考虑附件二以外其它变量的影响；
3、问题 4 进行单变量调整时，忽略其它变量的影响。

问题分析：

问题一分析
附件一提供了 10 个具有代表性水冷壁管道的温度值，采样周期为 15s，共 5000 组数据。首先我们检查了数据的完整性，在确保数据完整性的前提下分别绘制了 10 条水冷壁管道温度随时间变化的曲线，通过统计分析和观察获得曲线的变化趋势以及数据分布等信息。
问题二分析
首先，在实际生产过程中，希望水冷壁的温度变化尽可能平稳，我们计算各管道数据的方差，方差越小越稳定，表示数据间差别小、温度变化平稳。其次，为保证安全，水冷壁温度不宜过高。按照实际经验，操作人员给出的水冷壁温度超温报警线为 445℃。所以，需要对各管道的温度数据分布进行分析。
问题三分析
根据任务要求，利用附件 1 和附件 2 中的数据，建立水冷壁管道温度变化规律的数学模型，并对模型效果进行评估。想建立有效的数学模型，前提是要具有良好的数据可以使用。因为附件中 2 中的数据存在缺失值和异常值情况，而且样本特征过多，可能存在大量冗余的特征变量，以及与温度相关性很低的特征变量。所以，建模之前我们先利用数据挖掘技术对附件中的数据做预处理。然后，再建立水冷壁管道温度预测模型。
问题四分析
在实际生产过程中，为保证安全，水冷壁温度不宜过高，否则有烧坏的风险，按照实际经验，操作人员给出的水冷壁温度超温报警线为 445℃。图 7.1 显示的是第 10 个水冷壁管道温度曲线，在第 3172 个样本点后水冷壁出现明显的超温现象。根据题目要求，需要分析并定位出引发超温现象的主要操作变量。
问题五分析
在实际生产过程中，希望水冷壁的温度变化尽可能平稳，同时为保证安全，水冷壁温度不宜过高，否则有烧坏的风险。按照实际经验，操作人员给出的水冷壁温度超温报警线为 445℃。管道 10 在 3172 个样本后水冷壁出现明显的超温现象，而其余管道水冷壁温度趋于平缓，故管道 10 温度存在较大的优化空间。
在本文建立模型选取的 24 个特征中，其中有 10 维特征属于状态变量（原料、待生吸附剂、再生吸附剂），即它们的数值由附件一给定的样本数据确定，剩余 14 维操作变量作为目标函数的自变量参与寻优过程。根据本文在问题三中建立的模型作为目标函数，并计算附件 2 中特征的取值范围作为自变量的约束条件，通过寻优算法寻找目标函数最小值，同时输出此时的 24 维特征取值。解题过程分为数据预处理、建立数学模型、寻找特征变量最优取值、输出管道 10温度下降数值、计算。

模型的建立与求解整体论文缩略图

在这里插入图片描述

全部论文请见下方“ 只会建模 QQ名片” 点击QQ名片即可

程序代码：(代码和文档not free)

clc
clear
close all
data = xlsread('..\附件 1.xlsx');
data = data(:,2:11);
V = zeros(10,1);
for i = 1 : 10
 V(i,1)=var(data(:,i)) ;
end
count = zeros(10,1);
dataLen = length(data);
for i = 1 : 10
 for j = 1 : dataLen
 if data(j,i) >= 445
 count(i,1) = count(i,1) + 1; 
 end
 end
end
roi = zeros(10,2);
roi_cha = zeros(10,1);
for i = 1 : 10
 for j = 1 : dataLen
 roi(i,1) = min(data(:,i));
 roi(i,2) = max(data(:,i));
 roi_cha(i,1) = roi(i,2) - roi(i,1);
 end
end
zhongShu = zeros(10,1);
for i = 1 : 10
 zhongShu(i,1) = mode(data(:,i));
end
junZhi = zeros(10,1);
for i = 1 : 10
 junZhi(i,1) = mean(data(:,i));
end
zhongWeiShu = zeros(10,1);
for i = 1 : 10
 zhongWeiShu(i,1) = median(data(:,i));
end
disp('结束');

import pandas as pd
import numpy as np
import warnings
warnings.filterwarnings('ignore')
pd.set_option('display.max_columns', None)
train_df = pd.read_excel('./1_pre.xls', sep=' ')
# train_df = pd.read_excel('./1_pre.xls', sep=' ')
print(train_df.shape)
train_df.describe()
import matplotlib.pyplot as plt
import seaborn as sns
plt.figure()
sns.distplot(train_df['tunnel_10'])
plt.figure()
train_df['tunnel_10'].plot.box()
plt.show()
#数据分布图
import seaborn as sns
print('It is clear to see the price shows a typical exponential distribution')
plt.figure(figsize=(20,10))
plt.subplot(2,5,1)
sns.distplot(train_df['tunnel_1'])
plt.subplot(2,5,2)
sns.distplot(train_df['tunnel_2'])
plt.subplot(2,5,3)
sns.distplot(train_df['tunnel_3'])
plt.subplot(2,5,4)
sns.distplot(train_df['tunnel_4'])
plt.subplot(2,5,5)
sns.distplot(train_df['tunnel_5'])
plt.subplot(2,5,6)
sns.distplot(train_df['tunnel_6'])
plt.subplot(2,5,7)
sns.distplot(train_df['tunnel_7'])
plt.subplot(2,5,8)
sns.distplot(train_df['tunnel_8'])
plt.subplot(2,5,9)
sns.distplot(train_df['tunnel_9'])
plt.subplot(2,5,10)
sns.distplot(train_df['tunnel_10'])
num_cols = ['管道 10 温度', '再热蒸汽压力', 'C1 风粉一次风速', '水煤比', 'A3 风粉一次风
速', 'A1 风粉一次风速', 'A2 风粉一次风速','A4 风粉一次风速', '主汽压力', 'B1 风粉一次风速', 'B2 风粉一次风速', 'B3
风粉一次风速', 'B4 风粉一次风速', 
 'D2 风粉一次风速', 'D3 风粉一次风速', '分离器出口汽温过热度', '锅炉负荷
', '主蒸汽温度', '再热蒸汽温度', 'A 空预器出口二次风量 2', '锅炉给水温度 1', 
 '总风量流量', '总燃料量', '总给水流量', 'B 空预器出口二次风量 2', '#2 角摆
角燃烧器调节门反馈', '锅炉烟气含氧量', 
 '#1 角 AA 层二次风调节挡板位置反馈', '#2 角 AA 层二次风调节挡板位置
反馈', '#1 角摆角燃烧器调节门反馈', 
 '#3 角摆角燃烧器调节门反馈', 'A 给煤机给煤量反馈信号', '#2 角 A 层二次
风调节挡板位置反馈', 
 '#3 角 A 层二次风调节挡板位置反馈', '#4 角 A 层二次风调节挡板位置反馈
', '#1 角 A 层二次风调节挡板位置反馈', 
 'F 磨入口热一次风电调挡板位置', 'A 磨入口热一次风电调挡板位置', '#4 角
AB 层二次风调节挡板位置反馈', 
 '#1 角 AB 层二次风调节挡板位置反馈', '#2 角 AB 层二次风调节挡板位置
反馈', '#3 角 AB 层二次风调节挡板位置反馈', 
 '#2 角 EE 层二次风调节挡板位置反馈', '#4 角 EE 层二次风调节挡板位置反
馈']
# num_cols = ['省煤器出口温度 2', '锅炉负荷']
# cols = date_cols + cate_cols + num_cols
cols = num_cols
tmp = pd.DataFrame()
tmp['count'] = df[cols].count().values
tmp['missing_rate'] = (df.shape[0] - tmp['count']) / df.shape[0]
tmp['nunique'] = df[cols].nunique().values
tmp['max_value_counts'] = [df[f].value_counts().values[0] for f in cols]
tmp['max_value_counts_prop'] = tmp['max_value_counts'] / df.shape[0]
tmp['max_value_counts_value'] = [df[f].value_counts().index[0] for f in cols]
tmp.index = cols
tmp
#Spearman 相关系数 热度图
corr1 = abs(df[num_cols].corr(method='spearman',min_periods=1))
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
plt.figure(figsize=(20, 17))
sns.heatmap(corr1, linewidths=0.1, cmap=sns.cm.rocket_r)
#XGBoost 五折
## xgb-Model
xgr = xgb.XGBRegressor(n_estimators=120, learning_rate=0.1, gamma=0, subsample=0.8,\
 colsample_bytree=0.9, max_depth=7) #,objective ='reg:squarederror'
scores_train = []
scores = []
## 5 折交叉验证方式
sk=StratifiedKFold(n_splits=5,shuffle=True,random_state=0)
for train_ind,val_ind in sk.split(X_data,lista):
 train_x=X_data.iloc[train_ind].values
 train_y=Y_data.iloc[train_ind]
 val_x=X_data.iloc[val_ind].values
 val_y=Y_data.iloc[val_ind]
 xgr.fit(train_x,train_y)
 pred_train_xgb=xgr.predict(train_x)
 pred_xgb=xgr.predict(val_x)
 score_train = mean_absolute_error(train_y,pred_train_xgb)
 scores_train.append(score_train)
 score = mean_absolute_error(val_y,pred_xgb)
 scores.append(score)
print('Train mae:',np.mean(score_train))
print('Val mae',np.mean(scores))
plt.plot(pred_xgb,c='r',linestyle='-')
plt.plot(train_y,c='b',linestyle='-.')
# plt.plot(x3.cumsum(),c='b',linestyle=':',marker='*')
plt.legend(['pred_train_xgb','train_y'])
plt.show()