原题链接

题意分析

本题需要注意：

1. 等级限制比较复杂，可以最后考虑
2. 本题说 由 B物品 可以换 A物品，想到了B节点可以走到A节点，所以构建图
3. 由于我们是要买一个点再开始换的，所以我们可以构建一个源点，指向所有物品，表示直接购买该物品

所以样例构图如下

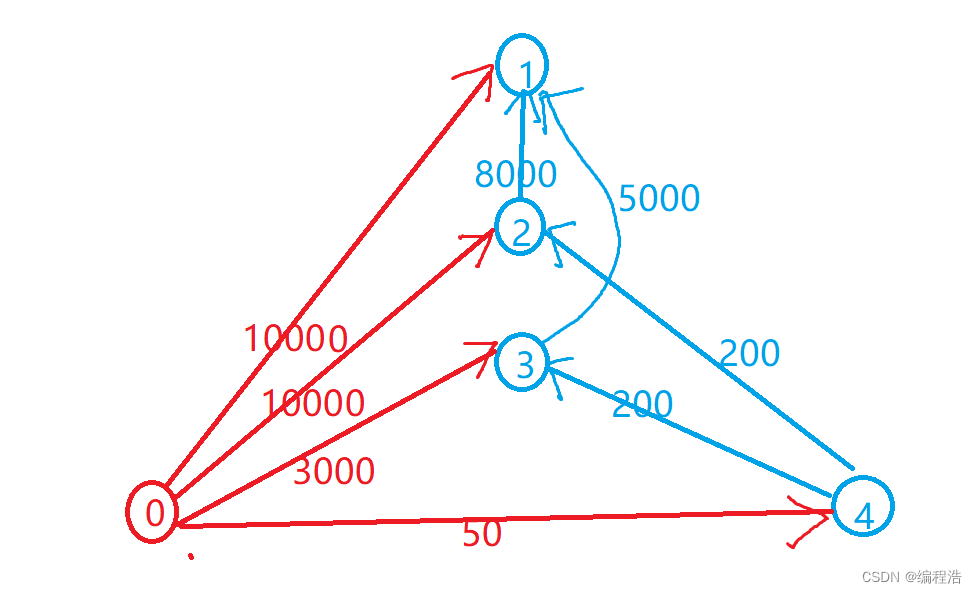
我们从0点开始dij，
得到dist数组，表示所有点到1节点的最短距离
那么dist[i]就表示最小花费了

问题还有一个就是：
等级制度怎么考虑？

首先我们必须买
大于首长等级-m的物品

那么出现一个问题就是

2 - 3 - 6 -5
2 - 4 - 5
现在比如 2 到 5
有这么两条路（2比3更便宜）

但是 2 不能 到 6

所以只能走 2 - 4 - 5

但是其实 3 - 6 - 5 总花费最小

所以只能多次dij

每次限制 等级区间

由于 1的等级是N
1是允许 N-m到N+m区间的

那么我们就从
N-m开始 每次是 N-m+m区间 逐渐+1
这样保证每次的路线都是合法的
然后多次dij取最小值即可

#include <cstring>
#include <iostream>
#include <algorithm>

using namespace std;

const int N = 110, INF = 0x3f3f3f3f;

int n, m;
int w[N][N], level[N];
int dist[N];
bool st[N];

int dijkstra(int down, int up)
{
    memset(dist, 0x3f, sizeof dist);
    memset(st, 0, sizeof st);

    dist[0] = 0;
    for (int i = 1; i <= n + 1; i ++ )
    {
        int t = -1;
        for (int j = 0; j <= n; j ++ )
            if (!st[j] && (t == -1 || dist[t] > dist[j]))
                 t = j;

        st[t] = true;
        for (int j = 1; j <= n; j ++ )
            if (level[j] >= down && level[j] <= up)
                dist[j] = min(dist[j], dist[t] + w[t][j]);
    }

    return dist[1];
}

int main()
{
    cin >> m >> n;

    memset(w, 0x3f, sizeof w);
    for (int i = 1; i <= n; i ++ ) w[i][i] = 0;

    for (int i = 1; i <= n; i ++ )
    {
        int price, cnt;
        cin >> price >> level[i] >> cnt;
        w[0][i] = min(price, w[0][i]);
        while (cnt -- )
        {
            int id, cost;
            cin >> id >> cost;
            w[id][i] = min(w[id][i], cost);
        }
    }

    int res = INF;
    for (int i = level[1] - m; i <= level[1]; i ++ ) res = min(res, dijkstra(i, i + m));

    cout << res << endl;

    return 0;
}