题目

对于一棵多叉树，我们可以通过 “左孩子右兄弟” 表示法，将其转化成一棵二叉树。

如果我们认为每个结点的子结点是无序的，那么得到的二叉树可能不唯一。

换句话说，每个结点可以选任意子结点作为左孩子，并按任意顺序连接右兄弟。

给定一棵包含 N​​ 个结点的多叉树，结点从 1​​ 至 N​ 编号，其中 1 号结点是根，每个结点的父结点的编号比自己的编号小。

请你计算其通过 “左孩子右兄弟” 表示法转化成的二叉树，高度最高是多少。

注：只有根结点这一个结点的树高度为 0​。

思路

最开始还以为是数学规律，看题解发现是去深度遍历每个节点的深度。每一层的节点存储在一个数组里面，由于使用左孩子右兄弟的表示法，则最高的高 = 该节点的孩子节点个数 + 孩子节点中最高的深度 

代码

import os
import sys
sys.setrecursionlimit(100000) #设置最深递归深度
# 请在此输入您的代码
N = int(input())
nodes = [[] for i in range(N+1)]
for i in range(2, N + 1): # 存储2​ 至 N 号结点的父结点编号
  j = int(input())
  nodes[j].append(i)

def dfs(i):
  if nodes[i] is None: #该层节点为空 即没有深度 返回0
    return 0
  
  maxn = 0
  for j in nodes[i]:#遍历第i层子节点的深度
    maxn = max(maxn, dfs(j))

  deep = maxn
  return len(nodes[i]) + deep # 第i层的子节点（每一个子节点变成二叉树都是一层高度） + 子节点中最深的深度

print(dfs(1))

题目

小明冒充 X 星球的骑士，进入了一个奇怪的城堡。

城堡里边什么都没有，只有方形石头铺成的地面。

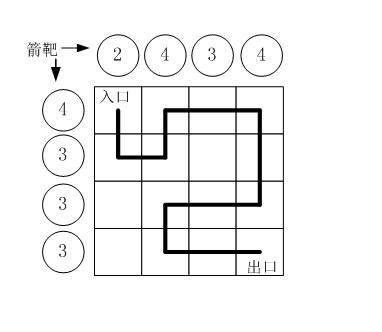
假设城堡地面是 n×n 个方格。如下图所示。

 

按习俗，骑士要从西北角走到东南角。可以横向或纵向移动，但不能斜着走，也不能跳跃。每走到一个新方格，就要向正北方和正西方各射一箭。（城堡的西墙和北墙内各有 n 个靶子）同一个方格只允许经过一次。但不必走完所有的方格。如果只给出靶子上箭的数目，你能推断出骑士的行走路线吗？有时是可以的，比如上图中的例子。

本题的要求就是已知箭靶数字，求骑士的行走路径（测试数据保证路径唯一）

思路

 使用dfs，多了一个判断西边和北边靶子上箭数目的条件。但是我还是不会写dfs，去查了题解，这个写得很清楚——>https://alex007.blog.csdn.net/article/details/90314923​​​​​​

有一个测试用例没有通过，超时了。 

代码 

import os
import sys

# 请在此输入您的代码
def dfs(r, c):
    """
    Args:
        r: 当前搜索行
        c: 当前搜索列
    Returns: Bool值，表示是否找到了一条符合条件路径
    """
    if r == n - 1 and c == n - 1: # 到达右下角
        if sum(north_target) > 0 or sum(west_target) > 0:  # 如果最后还有箭靶上面的数目不为零，也不符合要求
            return False
        path.append(r * n + c)
        print(' '.join(map(str, path)))
        return True

    path.append(r * n + c)
    direction = [(0, 1), (1, 0), (0, -1), (-1, 0)]
    for dr, dc in direction:
        nr, nc = r + dr, c + dc  # 下一个搜索位置的行、列

        # 保证下一个搜索的位置符合要求
        if -1 < nr < n and -1 < nc < n and not visit[nr][nc] and north_target[nc] > 0 and west_target[nr] > 0:
            visit[nr][nc] = True
            north_target[nc] -= 1
            west_target[nr] -= 1

            if dfs(nr, nc):
                return True
            else: #该路径走不通 则撤销刚才的操作 标记该点未被访问 靶数分别+1 路径将该点删除
                visit[nr][nc] = False
                north_target[nc] += 1
                west_target[nr] += 1

    path.pop()
    return False


if __name__ == '__main__':
    n = int(input())
    north_target = list(map(int, input().split()))
    west_target = list(map(int, input().split()))

    path = []
    visit = [[False] * n for _ in range(n)]  # 标记该点是否被访问过

    visit[0][0] = True
    north_target[0] -= 1
    west_target[0] -= 1
    dfs(0, 0)