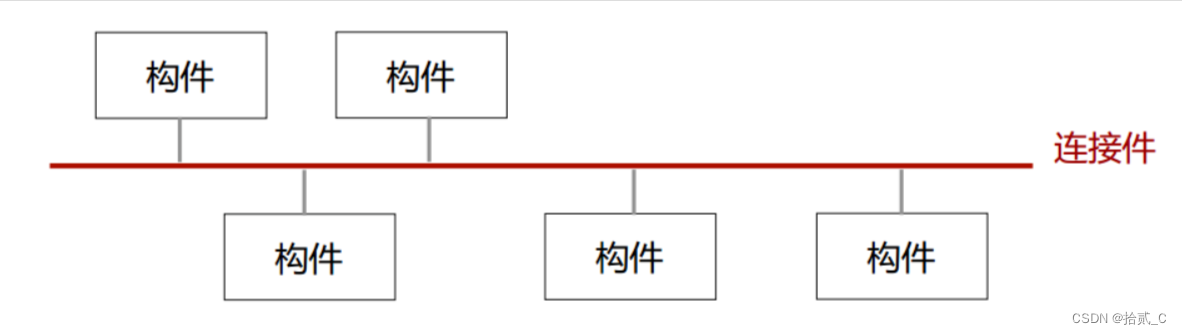
这篇主要讲栈(stack)和队列(queue)，实际要学习的数据结构有三个：stack、queue、priority_queue

这些数据结构已经不属于容器了，而是容器适配器。

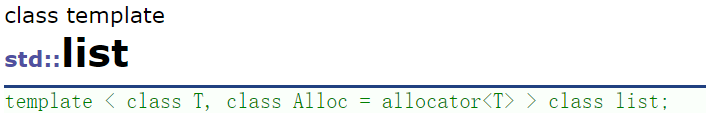
list的第二个参数是空间配置器，支持申请空间；而list和queue的第二个参数是一个叫Container的。具体是啥先不管。

看看queue和stack的说明：

由图可知，stack和queue不是自己实现的而是通过包装容器改造的。

queue的全部函数接口：

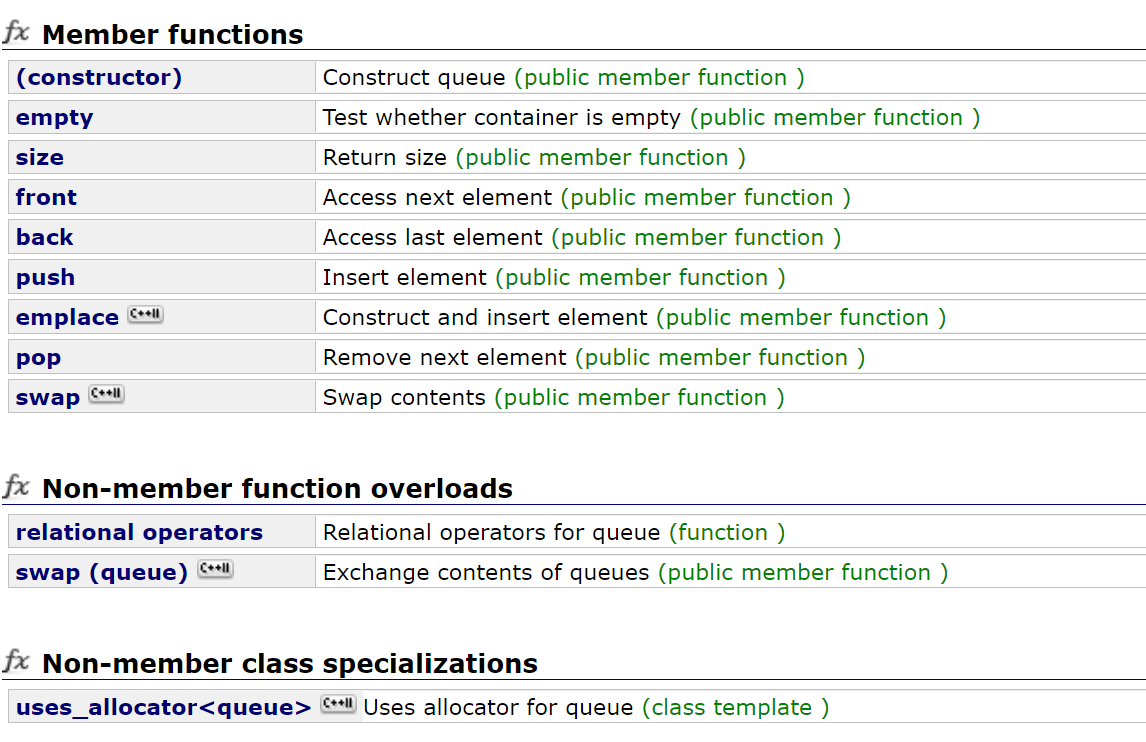
stack的全部函数接口：

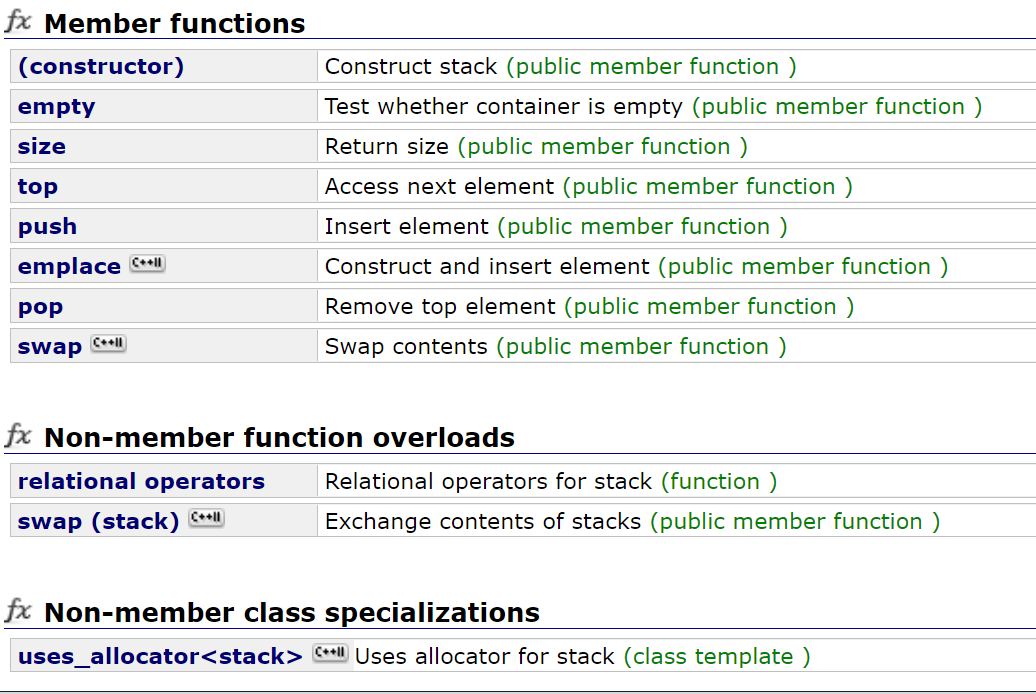
stack和queue连拷贝构造和析构都没有，因为默认生成的就够用，这点也和它是容器适配器有关：

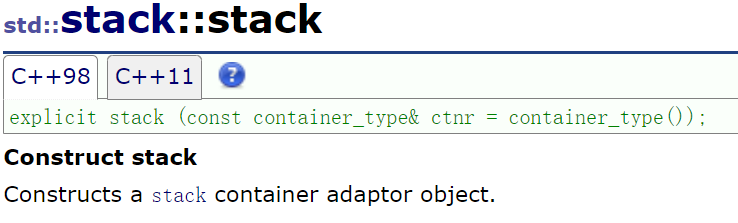
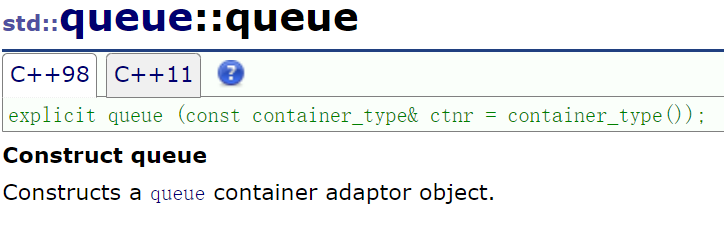
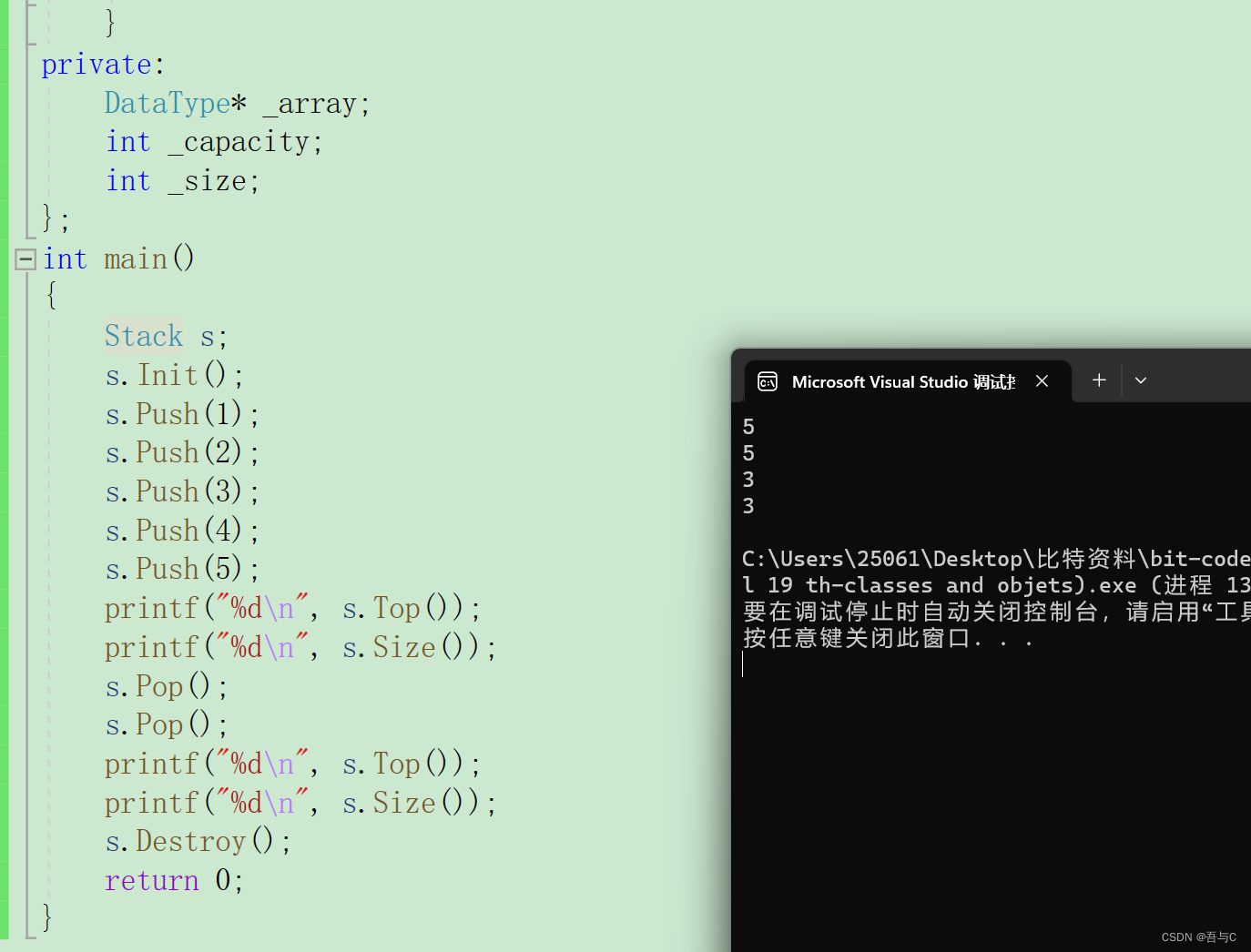
简单应用：

分别打印出：4 3 2 1  和  1 2 3 4

介绍一下优先级队列：priority_queue

heap意思是堆，priority_queue本质上就是一个堆，不是相似于堆。默认是一个大堆。

priority_queue的全部函数接口：

priority_queue的简单应用：

结果打印：8 6 5 2 1

在返回上面函数声明的部分，有一个很奇怪的点，默认传的仿函数为less，默认为大堆应该是greater才对。这里就理解成剩下的越来越小吧。仿函数的传递规则没有统一。

比如sort，排升序传less，排降序传greater。

如果要实现小堆应该这样：

greater是库里写好的仿函数，要包头文件：#include<functional>

栈的例题，力扣：栈的压入，弹出序列（题解写的不好，推荐自己练练）

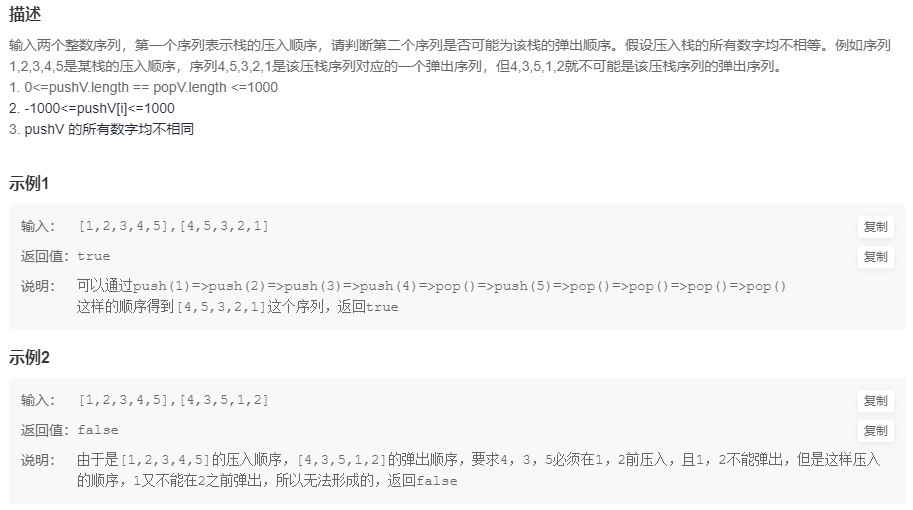
实现思路：

用一个栈，模拟出栈的压入，弹出，用变量popi指代应当出栈的位置，每次入栈后和第二序列中popi指向的内容进行比较，如果相等，popi后移一位，栈出栈，再次比较，直到不相等，或者第二序列结束；如果不相等，则代表数据还没有入栈，继续入栈。当入栈序列遍历结束后，如果栈内为空，则代表第二个序列可以为栈的弹出序列。如果栈内不为空，则代表出栈顺序不对，第二序列不为栈的弹出序列。

代码如下：

栈的例题，力扣：逆波兰表达式求值

逆波兰表达式又叫后缀表达式，用于计算器底层原理。正常见到的表达式是中缀表达式，即1+1+1+1。转换为后缀表达式后为：1 1 + 1 + 1 +。因为表达式的运算涉及到优先级问题（1+2*3，在读取到1+2时不能进行运算，因为后面可能有优先级更高的运算符），最底层的计算机只能顺序执行，所以中缀表达式要转换为后缀表达式后计算机才能进行运算。不过本题只需要对后缀表达式进行运算就可以了，不需要对中缀表达式进行转换。

解决思路：遇到数字，入栈；遇到操作符，连续取出栈的顶层两个元素，进行运算，运算结果继续入栈。运算的时候左右操作数不能随便设置，因为/和-有左右操作数要求。

代码如下：

下面介绍一下中缀表达式是如何转换成后缀表达式的

首先创建两个存储对象，一个为栈，存储操作符；一个为顺序储存对象，储存最终的后缀表达式。

遍历中缀表达式，遇到数字就存入后缀表达式，遇到运算符就和栈顶元素比较，如果栈顶元素没有或者比遍历到的运算符优先级低，遍历到的运算符就入栈；如果栈顶运算符比遍历到的运算符优先级高或者一样，就将栈顶运算符存入后缀表达式，栈顶运算符出栈，循环比较，直到栈内为空，或者栈顶运算符优先级比遍历到的优先级低，遍历到的运算符入栈。遍历结束，将栈内的运算符全部出栈，存入到后缀表达式中。

对运算符的操作和相邻的两个运算符有关。

以1 + 2 * 3 / 4 - 5为例（最好通过画图辅助理解）：遍历到1，存入后缀表达式，遍历到+，栈内为空，入栈，遍历到2，存入后缀表达式，遍历到*，和栈顶的+比较，入栈，遍历到3存入后缀表达式，遍历到/，和栈顶的*比较，*出栈，存入后缀表达式，/入栈，遍历到4存入后缀表达式，遍历到-，和栈顶的/比较，/出栈，存入后缀表达式，再和栈顶的+比较，+出栈，存入后缀表达式，此时栈内为空。-入栈，遍历到5，存入后缀表达式，遍历结束，栈内元素全部出栈。存入后缀表达式，最终后缀表达式为：1 2 3 * 4 / + 5 - 。运算验证一下，开始遇到*，栈内为1 2 3，即2*3运算，运算结束后栈内为1 6，然后遇到/，栈内为1 6 4，运算结束后为1 1，然后遇到+，运算结束栈内为2，遇到-，栈内为2 5，运算结束后栈内为-3。1 + 2 * 3 / 4 - 5的结果也是-3。

如果要考虑括号部分，就需要有一个标识变量flag来确定是否进入括号内，如果进入，则要认为此时的运算符优先级很高，需要入栈。