目录

300.最长递增子序列

思路

1、dp[i]的定义

2、递推公式 

3、dp数组初始化

4、确定遍历顺序

5、推导dp数组

最长递增子序列

674. 最长连续递增序列

思路

最长连续递增序列

动态规划

贪心算法

718. 最长重复子数组

思路

1、确定dp数组的含义

2、确定递推公式

3、dp数组初始化

4、遍历顺序

最长重复子数组

二维dp数组

一维dp数组

---

300.最长递增子序列

题目链接：力扣

思路

根据动态规划五部曲来对本题目进行分析

1、dp[i]的定义

        dp[i] 表示 i 之前(包括i)的以nums[i] 结尾的 最长递增子序列的长度

        目前来看，dp数组的定义都是按要求的结果来

2、递推公式 

        既然求得是递增得子序列，每一个元素下面代表的是自己目前代表的最大递增长度

        位置i的最长升序子序列等于j从0到i-1各个位置的最长升序子序列 + 1 的最大值

        从前向后进行遍历，遍历到当前元素，跟前面的每一个元素进行比较，如果比之前的某个元素大，那就说明以这个元素结尾的字符串递增子序列长度还能再 +1，所以可以得出递推公式：dp[i] = dp[j] + 1

        要从其中找出最长的一个子序列，所以：dp[ i ] = max(dp[ i ], dp[ j ] + 1) 

3、dp数组初始化

        对于每一个 i，对应的dp[i]，大小至少都是 1 .所以 dp 数组初始化都是1

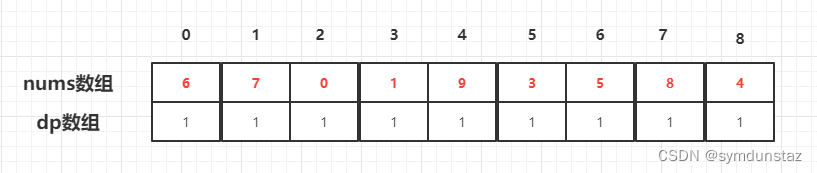
4、确定遍历顺序

        因为后面的长度都是根据前面的数字情况来的，所以，应该从后向前进行遍历

for (int i = 1; i < dp.length; i++) {
    for (int j = 0; j < i; j++) {
        if (nums[i] > nums[j]) {
            dp[i] = Math.max(dp[i],dp[j] + 1);
        }
    }
}

        外层遍历：i 是在移动数组下标，以每个元素结尾的 最大递增子序列 都要算出来

        内层遍历：j 是每次从 0 - (i - 1) 进行遍历
                         如果当前的数字 nums[i] 是大于  nums[i] ，那就说明这个最大递增子序列还能在增加，增加后的长度就是dp[j] + 1，赋值给 dp[i]
                          但是这个结果还不是固定的，nums[i] 要遍历完以下标 0 - (i - 1)  结尾的所有最大递增子序列，找最长的结尾

        动画模拟：最长上升子序列_哔哩哔哩

5、推导dp数组

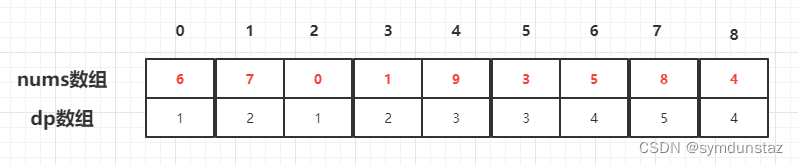
        这就像每一个元素，去最大自增子序列那里去竞聘，双向选择
        前面的子序列要选择比结尾还大的数字，对应代码中的if语句
        当前的元素要选择最长的长度，对应的就是递推公式

        举例说明：
        下标3，元素1，初始化是1，跟6比较，比6小，6不要它结尾
                                                     跟7比较，比7小，7不要它结尾
                                                     跟0比较，比0大，以0结尾的这个子序列可以以1结尾，如果以1结尾，以1 结尾的长度就是 1(以0结尾的长度) + 1 (多了元素3) = 2 ，所以 dp[3] = 2。
        再看看和目前代表的最大子序列长，max(1,2); 就获得了2
        ……

最长递增子序列

class Solution {
    public int lengthOfLIS(int[] nums) {

        // 创建dp数组
        int[] dp = new int[nums.length];

        // 初始化dp数组
        Arrays.fill(dp,1);

        // 推导dp数组
        for (int i = 1; i < dp.length; i++) {
            for (int j = 0; j < i; j++) {
                if (nums[i] > nums[j]) {
                    dp[i] = Math.max(dp[i],dp[j] + 1);
                }
            }
        }

        // 获取dp数组的最大值
        int result = 0;
        for (int num : dp) {
            result = Math.max(result,num);
        }

        return  result;
    }
}

674. 最长连续递增序列

题目链接：力扣

思路

        其实这道题比上一道题目简单很多，明白了上一道题目，这道题目就很简单了

        不连续递增子序列的跟前0-i 个状态有关，连续递增的子序列只跟前一个状态有关

最长连续递增序列

动态规划

class Solution {
    public int findLengthOfLCIS(int[] nums) {

        // 创建dp数组
        int[] dp = new int[nums.length];

        // 初始化dp数组
        Arrays.fill(dp,1);

        // 推导dp数组
        for (int i = 1; i < nums.length; i++) {
            if (nums[i] > nums[i-1]) {
                dp[i] = dp[i - 1] + 1;
            }
        }

        // 收获结果
        int result = 0;
        for (int num : dp) {
            result = num > result ? num : result;
        }

        return  result;
    }
}

贪心算法

class Solution {
    public int findLengthOfLCIS(int[] nums) {

        // 结果收集
        int result = 1;

        // 记录长度
        int count = 1; 

        for (int i = 1; i < nums.length; i++) {

            if (nums[i] > nums[i - 1]) {
                count++;
            } else {
                count = 1;
            }

            result = count > result ? count : result;
        }

        return  result;
    }
}

718. 最长重复子数组

题目链接：力扣

思路

        子数组，其实就是连续子序列

        这道题目确实不太好理解，可以看看这个图：力扣

1、确定dp数组的含义

        dp[i][j] : 以下标 i - 1为结尾的 A ，和下标为 j - 1为结尾的 B，最长重复子数组长度为dp[i][j]

2、确定递推公式

        dp[i][j] = dp[i - 1][j - 1] + 1

        这个递推公式确实不太好理解，可以把这道题目看成上一道题目的延申，这样就会发现这两个递推公式的相同之处，求连续的子序列，只跟前一个状态有关

3、dp数组初始化

        初始化为0

4、遍历顺序

        二维dp数组的内层循环和外层循环都是从前向后进行遍历

        一维dp数组的内层循环时从后向前进行遍历，因为计算当前值 依赖的是 其左上角的值，如果从前向后进行遍历，前面的结果有可能被覆盖掉了，后面就不能得到准确的值了

最长重复子数组

二维dp数组

// 写法一
class Solution {
    public int findLength(int[] nums1, int[] nums2) {
        
        // 创建dp数组
        int[][] dp = new int[nums1.length + 1][nums2.length + 1];

        // 初始化dp数组
        // 与默认值相符，不用初始化了

        int result = 0;

        // 推导dp数组
        for (int i = 1; i <= nums1.length; i++) {
            for (int j = 1; j <= nums2.length; j++) {
                if (nums1[i - 1] == nums2[j - 1]) {
                    dp[i][j] = dp[i - 1][j - 1] + 1;
                }

                result = dp[i][j] > result ? dp[i][j] : result;
            }
        }

        return result;
    }
}



// 写法二
class Solution {
    public int findLength(int[] nums1, int[] nums2) {

        int result = 0;

        // 创建dp数组
        int[][] dp = new int[nums1.length + 1][nums2.length + 1];

        // 推导dp数组
        for (int i = 0; i < nums1.length; i++) {
            for (int j = 0; j < nums2.length; j++) {
                if (nums1[i] == nums2[j]) {
                    dp[i + 1][j + 1] = dp[i][j] + 1;
                }

                result = Math.max(result,dp[i+1][j+1]);
            }
        }

        return  result;

    }
}

一维dp数组

class Solution {
    public int findLength(int[] nums1, int[] nums2) {
        
        // 创建dp数组
        int[] dp = new int[nums1.length + 1];

        // 初始化dp数组
        // 与默认值相符，不用初始化了

        int result = 0;

        // 推导dp数组
        for (int i = 1; i <= nums1.length; i++) {
            for (int j = nums2.length; j > 0; j--) {   // 注意遍历顺序
                if (nums1[i - 1] == nums2[j - 1]) {
                    dp[j] = dp[j - 1] + 1;
                } else {
                    dp[j] = 0;   // 注意 不相等的时候要重新赋值
                }

                result = dp[j] > result ? dp[j] : result;
            }
        }

        return result;
    }
}