正文

语句覆盖：每条语句至少执行一次。
判定覆盖：每个判定的所有可能结果至少出现一次。（又称“分支覆盖”）
条件覆盖：每个条件的所有可能结果至少执行一次。
判定/条件覆盖：一个判定中的每个条件的所有可能结果至少执行一次，并且每个判断本身的所有可能结果至少执行一次。
多重条件覆盖（组合覆盖）：每个判定中的所有可能的条件结果的组合，以及所有的入口点都至少执行一次。（注意“可能”二字，因为有些组合的情况难以生成。）
完全路径覆盖：每条路径至少执行一次。
基本路径覆盖：根据流图计算环复杂度，得到基本路径覆盖的用例数。
分割后的完全路径覆盖：每条路径至少执行一次，每个条件的所有可能结果至少执行一次。

覆盖程度

路径覆盖 > 多重条件覆盖 > 判定/条件覆盖 > 条件覆盖 > 判定覆盖 > 语句覆盖
1. 路径覆盖是覆盖率最高的。语句覆盖最弱。
2. 满足多重条件覆盖准则的测试用例集，同样满足判定覆盖准则、条件覆盖准则和判定/条件覆盖准则。

任何一种覆盖方法都无法实现完全的测试。所以，在实际的测试用例设计过程中，根据需要将不同的覆盖方法组合起来使用，以实现最佳的测试用例设计。

'假设有一个待测试的小程序，其Java源代码如下。使用以上白盒测试方法，完成对小程序的测试用例设计。'
public void foo (int a, int b, int x) {
    if(a>1 && b ==0) {
        x = x/a;
    }
 
    if (a==2 || x>1) {
        x = x+1;
    }
}

一、语句覆盖

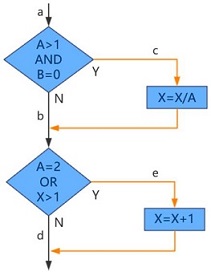
使用此准则测试上述小程序，只需要遍历路径ace，便将程序中的所有语句便都执行了一次。生成的用例及其遍历路径如下：

A=2，B=0，X=4 ace

缺点：语句覆盖是“最弱的覆盖”，它难以发现程序中的错误。①程序中存在一条x的值未发生改变的路径abd没有测试。②它无法发现判定的错误，比如第一个判定条件也许应该是“或”，而不是“与”。③无法发现条件的错误，比如第二个判断中的条件X>1，也许事实上应该是X>0。

二、判定覆盖

使用此准则测试小程序，只需要涵盖路径ace和abd，或涵盖路径acd和abe，就可以使得两个判定为“真”和为“假”的分支都执行一次。如果选择后一种情况，生成的用例及其遍历的路径如下：

A=3，B=0，X=3 acd
A=2，B=1，X=1 abe

我们仅有50%的可能性遍历到X值未发生改变的路径，即，只有我们选择涵盖路径ace和abd的情况，而不是涵盖路径acd和abe时。对应的测试用例如下：

A=2，B=0，X=2 ace
A=3，B=1，X=1 abd

缺点：这两组测试用例都存在同一个问题：当判定由多个条件组合构成时，它未必能发现每个条件的错误。如果第二个判定把条件X>1错误的写成了X<1，我们设计的测试用例仍然无法找出这个错误。

三、条件覆盖

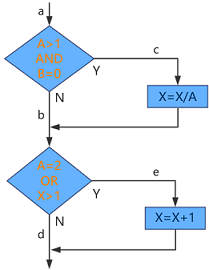
第一个判断的所有条件的可能取值情况是A>1或A≤1，B=0或B≠0。第二个判断的所有条件可能的取值情况为A=2或A≠2，X>1或X≤1。生成的用例及其遍历的路径如下所示：

A=1，B=0，X=3 abe
A=2，B=1，X=1 abe

缺点：条件覆盖并不一定总能覆盖全部分支。测试用例虽然满足了条件覆盖准则，但是只涵盖了程序的路径abe。但是，条件覆盖还是要比判定覆盖强一些，因为条件覆盖可能会使判断中各个条件的结果都取“真”或着取“假”，而判定覆盖却做不到这一点。

四、判定/条件覆盖

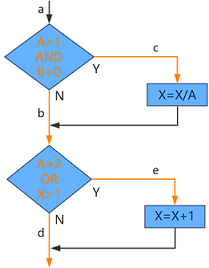
判定/条件覆盖，既要考虑到单个判定中每个条件的可能情况（A>1或A≤1，B=0或B≠0，A=2或A≠2，X>1或X≤1），也要考虑到每个判定的可能情况（路径ace和abd，或路径acd和abe）。用例及其遍历的路径如下所示：

A=2，B=0，X=4 ace
A=1，B=1，X=1 abd

缺点：条件覆盖和判定/条件覆盖不一定会发现逻辑表达式中的错误。尽管看上去所有条件的所有结果似乎都执行到了，但由于有些条件会屏蔽掉后面的条件，并不一定能全部执行得到。例如，上述测试用例①满足了条件A=2后，就不再执行对条件X>1的判断；测试用例②中不满足条件A>1后，就不再执行对条件B=0的判断。

五、多重条件覆盖

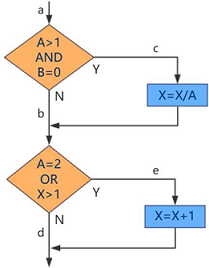
满足多重条件覆盖准则的测试用例，必须覆盖以下8种组合：

第一个判定的取值情况	第二个判定的取值情况
1. A>1，B=0	5. A=2，X>1
2. A>1，B≠0	6. A=2，X≤1
3. A≤1，B=0	7. A≠2，X>1
4. A≤1，B≠0	8. A≠2，X≤1

生成的测试用例，以及它们遍历的路径和覆盖的组合如下：

A=2，B=0，X=4 ace 覆盖组合1，5
A=2，B=1，X=1 abe 覆盖组合2，6
A=1，B=0，X=2 abe 覆盖组合3，7
A=1，B=1，X=1 abd 覆盖组合4，8

缺点：多重条件覆盖不一定能覆盖到每条路径，路径acd就被遗漏掉了。

六、路径覆盖

为了满足路径覆盖，必须首先确定具体的路径以及独立路径的个数。画出流程图。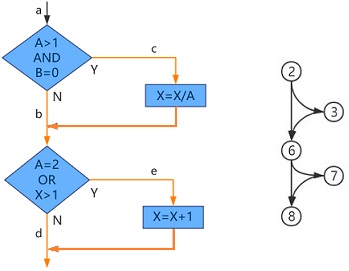

方法一：我们通常采用控制流图的边（弧）序列和节点序列表示某一条具体路径。
（1）弧a和弧b相乘，表示为ab，它表明路径是先经历弧a，接着再经历弧b。
（2）弧a和弧b相加，表示为a+b，它表明两条弧是“或”的关系，是并行的路段。
在路径表达式中，将所有弧均以数值1来代替，再进行表达式的相乘和相加运算，最后得到的数值即为该程序的独立路径数 = （1+1*1）*（1+1*1）= 2*2 = 4。

方法二：与弧的计算方式类似，还可以通过必经节点个数 i，再找出必经节点下的路径数 w(i) ，计算路径数。流程图中共有2个必经节点②⑥，且先经历②再经历⑥，没有并行的独立节点，独立路径数 = w(1)*...*w(i) = 2*2 = 4。

两种方法计算得到的路径数均为4条，它们分别覆盖了abd、abe、acd、ace：

A=1，B=0，X=1 abd
A=1，B=0，X=2 abe
A=3，B=0，X=1 acd
A=2，B=0，X=3 ace

缺点：（1）路径覆盖无法发现程序不符合设计规范的错误（需要借助于黑盒测试的外部规格说明书）。比如，① 不一定发现路径本身的错误（缺一条或多一条路径）；② 可能不会暴露数据敏感的错误（比如计算两数之差小于某个值，如果程序实现的是a-b<c，而不是|a-b|<c，那么当b-a>c时则无法发现程序的逻辑错误。）。所以，建议先使用黑盒方法设计测试用例，再使用白盒方法对用例进行补充。
（2）路径覆盖不一定把所有的条件组合情况都覆盖。以上测试用例尽管从表面上看已经满足路径覆盖，可是却无法发现程序当条件语句中的B=0误写为B>=0时的错误，即没有对B≠0的情况进行测试。另外，第4个用例中由于A=2，第二个判定中的X>1条件被忽略，虽然覆盖了路径abd，却无法发现X>1误写为X>2时的错误，即没有对覆盖ace路径时X>1的情况进行测试。
（3）复杂程序的用例数呈指数级上升。假设一段程序有10条判断语句，则i=10， w(i)=2，独立路径数为2的10次方，即1024，则要为它设计1024个测试用例。

七、完全路径覆盖

完全路径即所有独立路径的集合；非完全路径，即所有独立路径集合的真子集。前面列出的独立路径集合并非完全路径，因为前面的流程图中含有隐含路径。

因此，如果判断中的条件表达式是由一个或多个逻辑运算符 (OR, AND, NAND, NOR)连接的复合条件表达式，则需要改为一系列只有单条件的嵌套的判断。细化后不含隐含路径的控制流图和流程图见下。

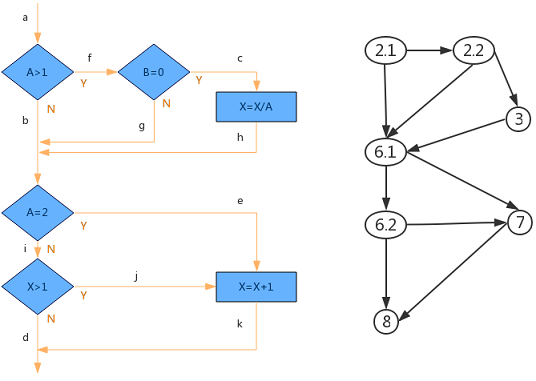
独立路径数 = (1+1*1+1*1)*(1*1+1*1*1+1*1) = 3*3 = 9。
或者，必经节点有两个（节点2.1和节点6.1），独立路径数 = w(1)*w(2) = 3*3 = 9。

路径一：2.1→6.1→6.2→8
路径二：2.1→6.1→6.2→7→8
路径三：2.1→6.1→7→8
路径四：2.1→2.2→6.1→6.2→8
路径五：2.1→2.2→6.1→6.2→7→8
路径六：2.1→2.2→6.1→7→8
路径七：2.1→2.2→3→6.1→6.2→8
路径八：2.1→2.2→3→6.1→6.2→7→8
路径九：2.1→2.2→3→6.1→7→8

由此，要达到完全路径覆盖就需要设计9个测试用例，去掉不可能的情况路径三（因为A不可能同时满足A≤1，A=2两个条件），仍然有8个用例。尽管在消除隐藏条件后解决了路径覆盖中的问题（2），但是完全路径覆盖的测试量比之前更加庞大。

八、基本路径覆盖

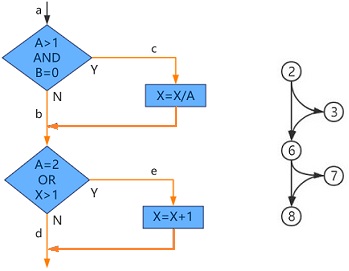
计算圈复杂度的三种公式	说明
V(G) = e - n + 2	e为边数，n为节点个数
V(G)=P+1	P为判定节点的个数
V(G)=区域数	闭合区域+开放区域

V(G) = 6-5+2 = 3
V(G) = 2+1 = 3
V(G) = 2个闭合区域+1个开放区域 = 3
无论使用哪种方法计算，都可确定3条独立的路径，即基本路径覆盖的用例数。

路径一：②⑥⑧，测试数据A=1，B=0，X=1 abd
路径二：②③⑥⑧，测试数据A=3，B=0，X=1 acd
路径三：②⑥⑦⑧，测试数据A=1，B=0，X=2 abe

思考：为什么②⑥⑧，②③⑥⑦⑧两个用例就可以将从②到⑧的路径全部覆盖，基本路径覆盖计算的结果还需要三个用例？我个人理解的原因是基本路径覆盖的一个测试用例一次只有一个变量因子。比如路径二相对路径一只有节点③发生了改变，路径三相对路径一只有节点⑦发生了改变。而如果只有②⑥⑧，②③⑥⑦⑧两个用例，虽然覆盖到了全部路径，但一次有两个因子③和⑦都发生了变化，无法对单个条件变化的测试结果进行比对。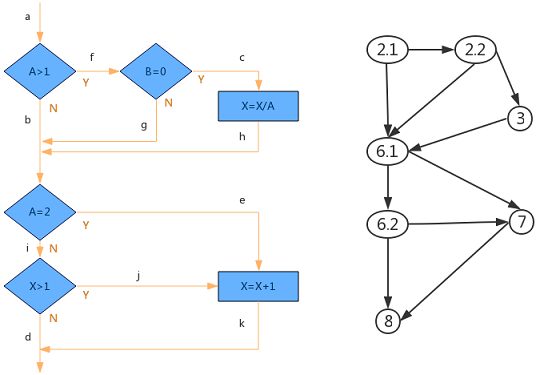

V(G) = 10-7+2 = 5
V(G) = 4+1 = 5
V(G) = 4个闭合区域+1个开放区域 = 5
无论使用哪种方法计算，都可确定5条独立的路径，即基本路径覆盖的用例数。

路径一：2.1→6.1→6.2→8，测试数据A=1，B=0，X=1 abid
路径二：2.1→2.2→6.1→6.2→8，测试数据A=3，B=1，X=1 afgid
路径三：2.1→2.2→3→6.1→6.2→8，测试数据A=3，B=0，X=1 afchid
路径四：2.1→6.1→7→8，测试数据A=？，B=？，X=？ abek

路径五：2.1→6.1→6.2→7→8，测试数据A=1，B=0，X=2 abijk

设计测试数据时发现“路径四”abek不可能存在（因为A不可能同时满足A≤1，A=2两个条件），根据实际情况调整路径为afgek，对应的测试数据为A=2，B=1，X=1。

缺点：尽管基本路径覆盖用例已经比完全路径覆盖的用例少了许多，但是当语句中有很多线性判定条件时，仍然无法解决测试量指数上升的问题。

九、分割后的完全路径覆盖

如果消除隐藏路径后，将程序在必经节点处割断，分别对每一段程序进行完全路径覆盖的充分测试，则即达到了完全路径覆盖的目的，又能对必经节点中的每个条件都进行考量，还大大减少了测试用例量。

分割后的控制流图和流程图

第一段程序的取值情况	第二段程序的取值情况
A≤1，B=任意值，X=任意值 `ab`	A≠2，X≤1 `oid`
A>1，B≠0，X=任意值 `afg`	A=2，X=任意值 `oek`
A>1，B=0，X=任意值 `afch`	A≠2，X>1 `oijk`

综合以上条件，得到测试用例如下：

A=1，B=0，X=1 aboid 输出：A=1，B=0，X=1
A=2，B=1，X=1 afgoek 输出：A=1，B=0，X=2
A=3，B=0，X=6 afchoijk 输出：A=1，B=0，X=2

最终得到的用例数为3，比程序被分割之前的所需用例数少了很多，缓解了测试量过大的问题；另一方面，针对两个程序片段实现了完全路径覆盖，解决了测试不足的问题。前面所提到的不一定覆盖所有条件组合情况下的BUG（未测试到的B≠0，X>1的情况，即将B=0误写为B>=0，X>1误写为X>2的错误），将会被测试用例2和测试用例3发现。

优点：分割后的完全路径覆盖方法，解决了前面所说的第（2)、(3）问题，不仅对条件语句的每种情况都进行了考量，还防止了测试用例呈指数级上升的可能，解决了测试不足和测试量过大之间的矛盾。

十、基本路径覆盖和分割后的完全路径覆盖用例对比

编号	A	B	X	路径	编号	A	B	X	路径
(1)	1	0	1	`abid`	(1)	1	0	1	`abid`
(2)	3	1	1	`afgid`
(3)	3	0	1	`afchid`
(4)	2	1	1	`afgek`	(2)	2	1	1	`afgek`
(5)	1	0	2	`abijk`
					(3)	3	0	6	`afchijk`

基本路径用例(2)测试的是A>1，B≠0，X≤1的情况，在分割后的完全路径覆盖用例(2)中覆盖了A>1，B≠0的情况，在分割后的完全路径覆盖用例(1)中覆盖了X≤1的情况。
基本路径用例(3)测试的是A>1，B=0，X≤1的情况，在分割后的完全路径覆盖用例(3)中覆盖了A>1，B=0的情况，在分割后的完全路径覆盖用例(1)中覆盖了X≤1的情况。
基本路径用例(5)测试的是A≤1，B值忽略，X>1的情况，在分割后的完全路径覆盖用例(1)中覆盖了A≤1，B值忽略，在分割后的完全路径覆盖用例(3)中覆盖了X>1的情况。

结论：基本路径覆盖对比起分割后的完全路径覆盖方法，后者不但实现了路径覆盖，还考虑到了条件语句的每种情况，并且用例数比基本路径覆盖更为精简，解决了完全路径覆盖和基本路径覆盖中复杂程序用例呈指数级上升的问题。

最后感谢每一个认真阅读我文章的人，礼尚往来总是要有的，虽然不是什么很值钱的东西，如果你用得到的话可以直接拿走：