• T检验通常分为三种：单样本T检验、双样本T检验、配对样本T检验
• 原理可以参考：一文详解t检验
• 本文主要介绍使用python实现T检验的过程，内容主要是参考这篇博文：利用python库stats进行t检验

一、单样本T检验

• 目的：检验单样本的均值是否和已知总体的均值相等

• 前提条件：
  （1）总体方差未知，否则就可以利用 $Z$ 检验（也叫 $U$ 检验，就是正态检验）；
  （2）正态数据或近似正态；
  （3）连续变量

• 原假设和备择假设：
  $$\begin{array}{rl}& H_0:样本均值（\overline{X}）和总体均值（\mu ）相等\\ & H_1:样本均值（\overline{X}）和总体均值（\mu ）不相等\end{array}$$

• 例子：假设已知我国男青少年的平均身高是1.73，那么取某高校50名男生的身高（本文采用随机数据），想比较该高校与我国男青少年的平均身高是否存在差异。

ttest_1samp 函数参数可参考：Python scipy.stats.ttest_1samp实例讲解

from scipy import stats
 
rvs = stats.norm.rvs(loc=1.5, scale=1, size=(50)) # 生成均值为1.5，标准差为1的50个样本
t, p = stats.ttest_1samp(rvs, 1.73)               # 进行单样本T检验

print(" T-test: %f\n"%t,"P-vlaue: %f"%p)

# T-test: -3.087647
# P-vlaue: 0.003317

结论：T值小于0，说明样本均值小于总体均值；P值小于0.05，说明该高校与我国男青少年的平均身高存在差异。

• 单侧检验 ：scipy库中stats只提供了双侧检验，如果需要单侧检验只需要将计算出来的P值除于2即可，这里参考文章：利用python进行单边T检验

• 置信区间：采用 scipy.stats.norm.interval() 函数计算

import numpy as np

stats.norm.interval(
    alpha = 0.95,
    loc = np.mean(rvs),
    scale = stats.sem(rvs)
)

二、独立样本t检验（双样本T检验）

• 目的：检验两组独立样本均值是否相等
• 前提条件：
  （1）两组总体方差相等，如果不相等，先利用levene检验，检验两总体是否具有方差齐性；
  （2）正态数据或近似正态；
  （3）连续变量
• 原假设和备择假设：
  $$\begin{array}{rl}& H_0:两独立样本均值相等\\ & H_1:两独立样本均值不相等\end{array}$$

场景1： 想比较可口可乐饮料在沃尔玛、大润发两个超市的销量是否存在差异
场景2： 想比较南、北方人的平均身高、体重是否存在差异

需要注意的是：前期需要检验两组方差是否相等，如不相等， scipy.stats.ttest_ind() 函数中的参数 equal_var 需要设置成 False

• levene 检验P值 > 0.05，接受原假设，认为两组方差相等

from scipy import stats
 
rvs_1 = stats.norm.rvs(loc=1.5, scale=1, size=(50)) # 生成均值为1.5，标准差为1的50个样本
rvs_2 = stats.norm.rvs(loc=2, scale=1, size=(50))   # 生成均值为2，标准差为1的50个样本

levene = stats.levene(rvs_1, rvs_2)                 # 进行 levene 检验

t, p = stats.ttest_ind(rvs_1,rvs_2,equal_var=True) # 独立样本t检验

print("levene 检验P值: %f"%levene.pvalue,'\n')

print("独立样本t检验")
print(" T-test: %f\n"%t,"P-vlaue: %f"%p)

• T值小于0，说明第一组数据的均值小于第二组
• 单侧检验：同上

三、配对样本T检验

• 目的：比较同一组样本在不同场景下，均值是否存在差异
• 前提条件：
  （1）两组总体方差相等，如果不相等，先利用levene检验，检验两总体是否具有方差齐性；
  （2）正态数据或近似正态；
  （3）连续变量
• 原假设和备择假设：
  $$\begin{array}{rl}& H_0:两配对样本均值相等\\ & H_1:两配对样本均值不相等\end{array}$$

场景1： 将小白鼠配对为两组，分别接受不同的处理，检验处理结果的差异
场景2： 对于一批血清样本，将其分为两个部分，利用不同的方法接受某种化合物的检验，检验结果的差异
场景3： 检验癌症患者术前、术后的某种指标的差异
场景4： 可口可乐饮料今年与去年在沃尔玛超市销售额均值是否存在差异

与独立样本t检验相比，配对样本T检验要求样本是配对的，两个样本的样本量要相同

python 实现有两种方式：
（1）两组数据做差，再对差值进行单样本T检验，检验均值为0;
（2）利用 scipy.stats.ttest_rel() 函数进行配对样本T检验

from scipy import stats
 
rvs_1 = stats.norm.rvs(loc=1.5, scale=1, size=(50)) # 生成均值为1.5，标准差为1的50个样本
rvs_2 = stats.norm.rvs(loc=2, scale=1, size=(50))   # 生成均值为2，标准差为1的50个样本

levene = stats.levene(rvs_1, rvs_2)          # 进行 levene 检验
t1, p1 = stats.ttest_1samp(rvs_1 - rvs_2, 0) # 单样本T检验
t2, p2 = stats.ttest_rel(rvs_1,rvs_2)        # 配对样本t检验

print("levene 检验P值: %f"%levene.pvalue,'\n')

print("单样本T检验")
print(" T-test: %f\n"%t1,"P-vlaue: %f"%p1)

print("\n配对样本t检验")
print(" T-test: %f\n"%t2,"P-vlaue: %f"%p2)

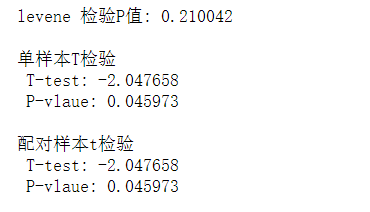
• T值小于0，说明第一组数据的均值小于第二组
• 单侧检验：同上