游程编码

游程编码（Run Length Coding，简称RLC）又称游程编码、行程长度编码、变动长度编码 等，是一种统计编码。主要技术是检测重复的比特或字符序列，并用它们的出现次数取而代之。比较适合于二值图像的编码，但是不适用于连续色调阁像的压缩，例如日常生活中的照 片。为了达到较好的压缩效果，有时行程编码和其他一些编码方法混合使用。

该编码属于无损压缩编码，是栅格数据压缩的重要编码方法。对于二值图有效。该压缩编码技术相当直观和经济，运算也相当简单，因此解压缩速度很快。RLE压缩编码尤其适用于计算机生成的图形图像，对减少存储容量很有效果。

RLC的基本原理是：用一个符号值或串长代替具有相同值的连续符号（连续符号构成了一段连续的“行程”。行程编码因此而得名），使符号长度少于原始数据的长度。

基本介绍

行程编码（Run-length Coding)是相对简单的编码技术，主要思路是将一个相同值 的连续串用一个代表值和串长来代替。例如，有一个字符串“aaabccddddd”，经过行程 编码后可以用“3a1b2c5d”来表示。对图像编码来说，可以定义沿特定方向上具有相同灰度值的相邻像素为一轮，其延续长度称为延续的行程，简称为行程或游程。例如，若沿水平方向有一串M个像素具有相同的灰度N，则行程编码后，只传递2个值（N,M) 就可以代替M个像素的M个灰度值N。

此方式下每两个字节组成一个信息单元。第一个字节给出其后面相连的象素的个数。第二个字节给出这些象素使用的颜色索引表中的索引。例如：信息单元03 04，03表示其后的象素个数是3个，04表示这些象素使用的是颜色索引表中的第五项的值。压缩数据展开后就是04 04 04 .同理04 05 可以展开为05 05 05 05. 信息单元的第一个字节也可以是00，这种情况下信息单元并不表示数据单元，而是表示一些特殊的含义。这些含义通常由信息单元的第二个字节的值来描述。
行程编码对传输差错很敏感，如果其中一位符号发生错误，就会影响整个编码序列的正确性，使行程编码无法还原回原始数据，因此一般要用行同步、列同步的方法.把差错控制 在一行一列之内。

示例1

例如：5555557777733322221111111。行程编码为：（5，6）（7，5）（3，3）（2，4）（l，7）。可见，行程编码的位数远远少于原始字符串的位数。

示例2

在对图像数据进行编码时，沿一定方向排列的具有相同灰度值的像素可看成是连续符号，用字串代替这些连续符号，可大幅度减少数据量。行程编码是连续精确的编码，在传输过程中，如果其中一位符号发生错误，即可影响整个编码序列，使行程编码无法还原回原始数据。

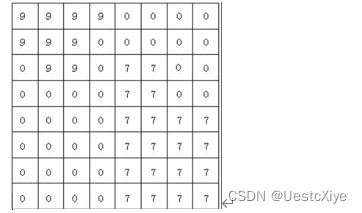
对如上图所示的栅格数据，可沿行方向进行如下游程长度编码： (9,4),(0,4),(9,3),(0,5),(0,1)(9,2),(0,1),(7,2),(0,2),(0,4),(7,2),(0,2),(0,4),(7,4),(0,4),(7,4) ,(0,4),(7,4) ,(0,4),(7,4)。游程长度编码只用了40个整数就可以表示，而如果用前述的直接编码却需要64个整数表示，可见游程长度编码压缩数据是十分有效又简便的。事实上，压缩比的大小是与图的复杂程度成反比的，在变化多的部分，游程数就多，变化少的部分游程数就少，图件越简单，压缩效率就越高。

游程长度编码在栅格加密时，数据量没有明显增加，压缩效率较高，且易于检索，叠加合并等操作，运算简单，适用于机器存贮容量小，数据需大量压缩，而又要避免复杂的编码解码运算增加处理和操作时间的情况。

游程编码适用的场景

算法的基本思想是将重复且连续出现的字符进行压缩，使用更简短的方式来描述，这种方式是基于柯氏复杂度的，那么什么是柯氏复杂度呢，比如有这么三个字符串，它们的长度都是100，其中第一个是100个A，第二个是99个A和一个B，第三个是100个完全随机的字符，我们想办法用尽可能短的语言来描述原字符串，描述第一个字符串时可以说“这是100个A”，描述第二个字符串可以说“这是99个A，然后是一个B”，但是描述第三个字符串时应该怎么说呢？比较容易想到的是“这是100个随机字符”，看上去似乎没有问题，但是这里一个比较重要的点是描述信息需要符合这么一个条件，当单独给出对字符串的描述时能够根据描述恢复出原字符串的内容，100个A和先99个A然后是一个B可以，但是100个随机字符太笼统了显然不行，这个描述信息的长度就称之为柯氏复杂度，在这个例子中第一个柯氏复杂度最小，第二第三依次次之。

那么在不同情况下这个编码的效果如何呢，假如采用定长1个字节来描述连续出现次数，并且一个字符占用1个字节，那么描述（连续出现次数，某个字符）需要的空间是2个字节，只要这个连续出现次数大于2就能够节省空间，比如AAA占用3个字节，编码为(3,A)占用两个字节，能够节省一个字节的空间，可以看出连续出现的次数越多压缩效果越好，节省的空间越大，对一个字符编码能够节省的空间等于=连续出现次数-2，于是就很容易推出连续出现次数等于2时占用空间不变，比如AA占用两个字节，编码为（2,A）仍然占用两个字节，白白浪费了对其编码的资源却没有达到节省空间的效果，还有更惨的情况，就是连续出现次数总是为1，这个时候会越压越大，比如A占用一个字节，编码为(1,A)占用两个字节，比原来多了一个字节，这种情况就很悲剧，一个1M的文件可能一下给压缩成了2M（真是效果奇佳啊），这是能够出现的最糟糕的情况，相当于在文件的每一个字节前面都插入了一个多余的字节0X01（这个字节表示连续出现次数为1），这种情况说明不适合使用游程编码，事实上，绝大多数数据的特征都属于第三种情况，不适合使用游程编码。