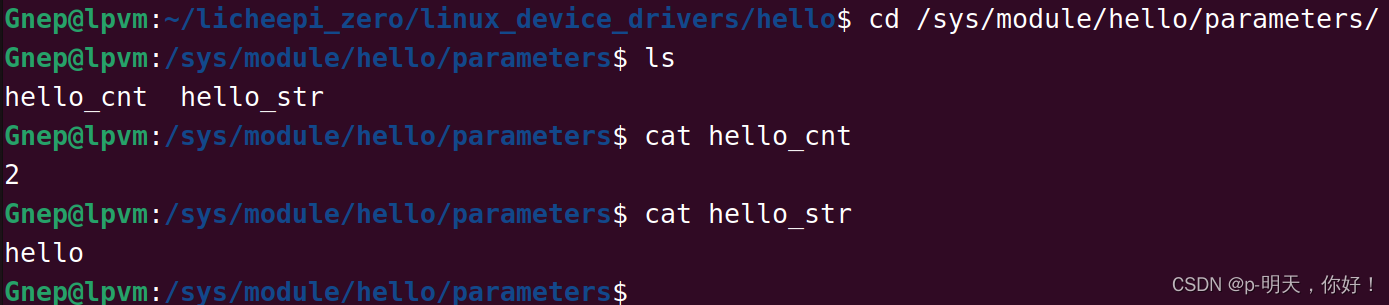
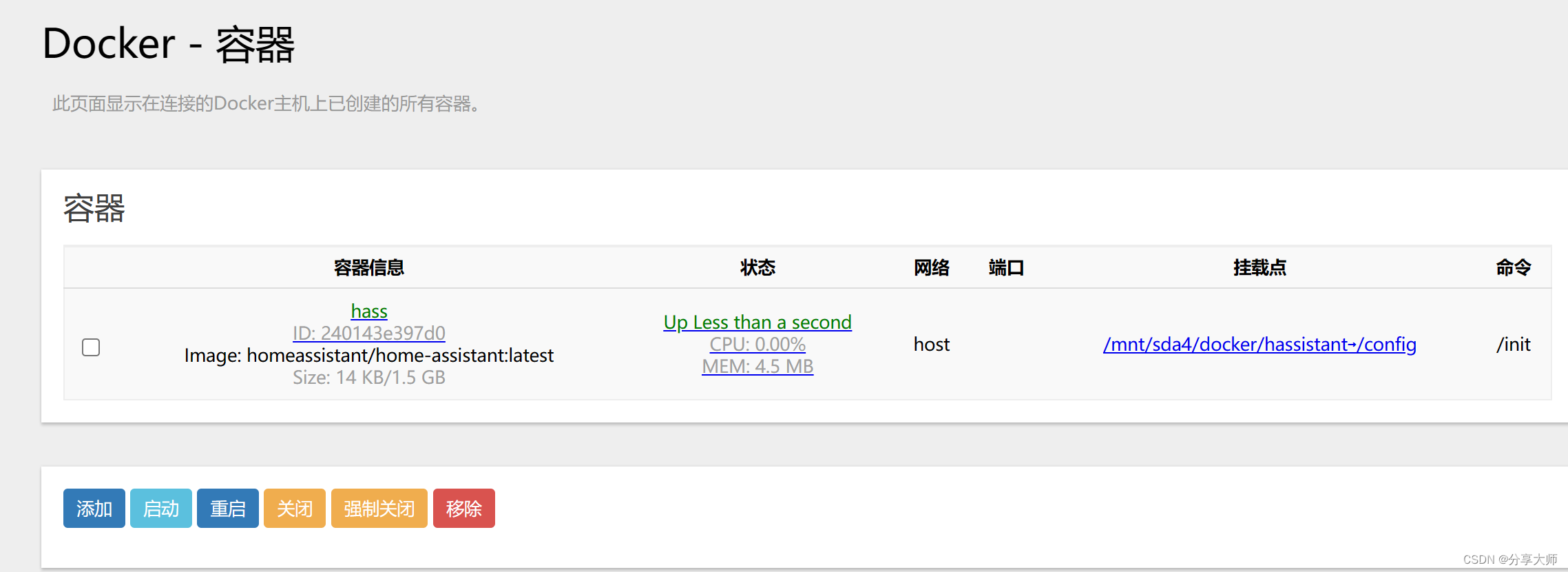
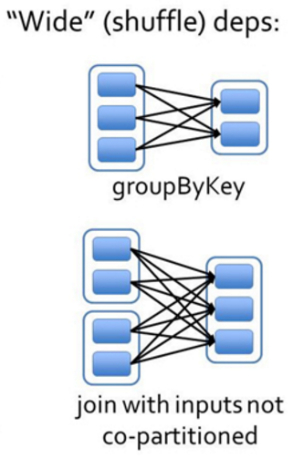
Problem - 9D - Codeforces

题意：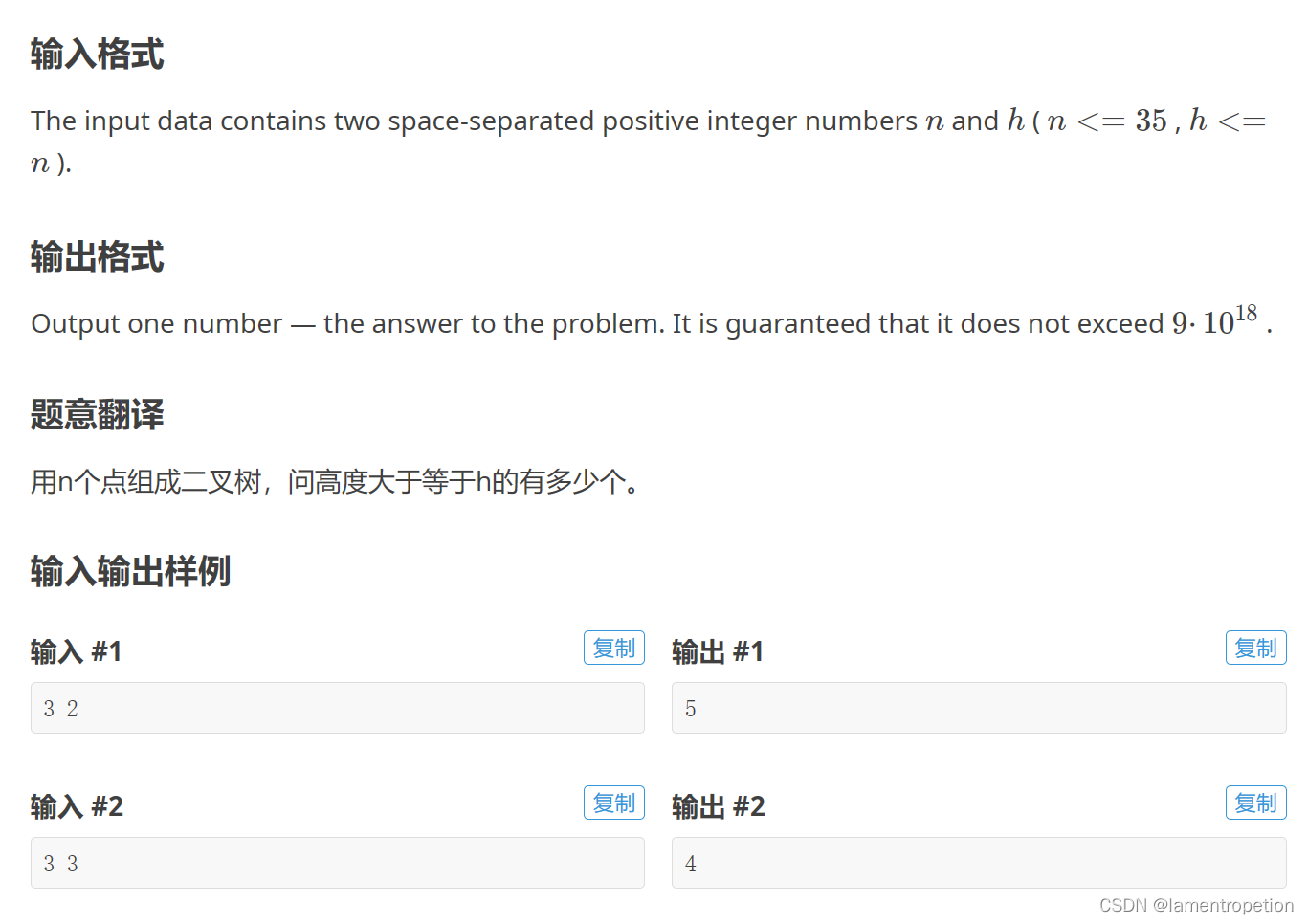

思路：

计数问题，考虑计数DP

因为它是二叉树，比较特殊，所以可以考虑一下线性DP
按照题目最后要算的答案，状态可以这样设计：

设dp[i][j]表示树高为i，结点数<=j的方案数

它其实就是按照树高为阶段的DP

怎么去转移呢

如果我们按照最后一层，即都是叶子结点的那一层来转移，发现根本不知道怎么算贡献

关于树的DP，一般都是以子树作为主体的

如果我们按照最上面那一层转移，就会发现，转移的过程中，DP的主体就是子树

 这样就很好转移了

dp[i][j]为树高是i,总结点数是j的方案数，主体是整棵树

dp[i-1][j]为树高是i-1（去掉第一层）,总结点数是j的方案数，此时这个DP数组的主体就是根节点的两棵子树

这样转移方程就是：

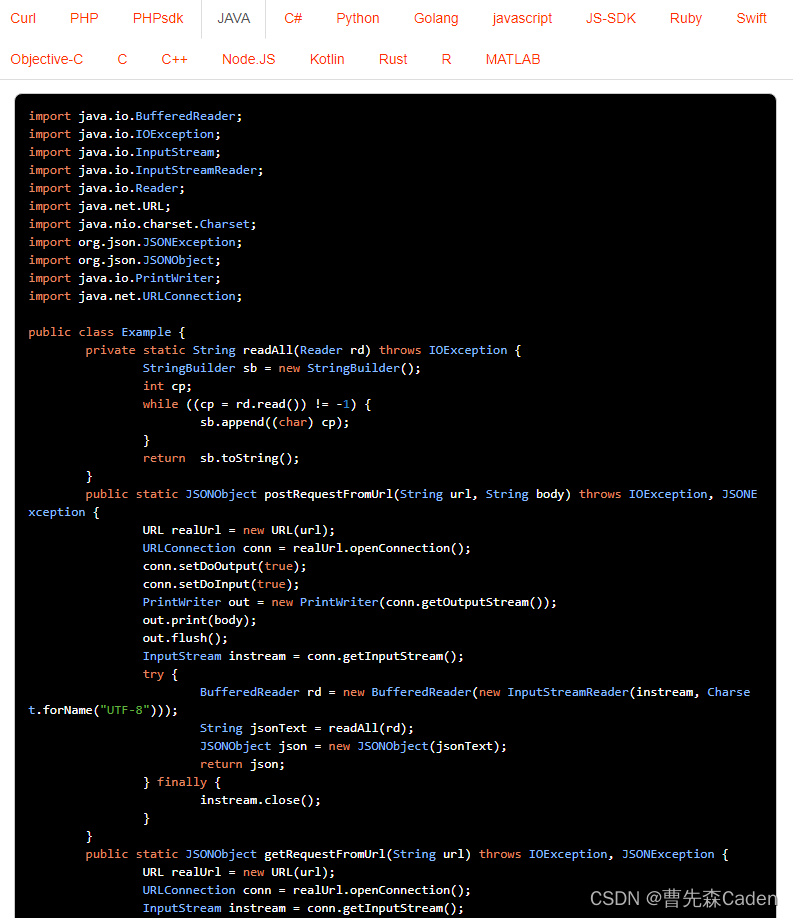
Code：

#include <bits/stdc++.h>

#define int long long

using namespace std;

const int mxn=1e2+10;
 
int N,h;
int dp[mxn][mxn];//树高为i，该树除了子树根节点的子树有j个结点的方案数

void solve(){
    cin>>N>>h;
    for(int i=0;i<=N;i++) dp[i][0]=1ll;
    for(int i=1;i<=N;i++){
        for(int j=1;j<=N;j++){
            for(int k=0;k<j;k++){
                dp[i][j]+=dp[i-1][k]*dp[i-1][j-k-1];
            }
        }
    }
    cout<<dp[N][N]-dp[h-1][N]<<'\n';
}
signed main(){
    ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
    int __=1;//cin>>__;
    while(__--)solve();return 0;
}