1 理论基础
在实际工程优化问题中,多数问题是多目标优化问题。相对于单目标优化问题,多目标优化问题的显著特点是优化各个目标使其同时达到综合的最优值。然而,由于多目标优化问题的各个目标之间往往是相互冲突的,在满足其中一个目标最优的同时,其他的目标往往可能会受其影响而变得很差。因此,一般适用于单目标问题的方法难以用于多目标问题的求解。
多目标优化问题很早就引起了人们的重视,现已经发展出多种求解多目标优化问题的方法。多目标优化问题求解中最重要的概念是非劣解和非劣解集,两者的定义如下。
非劣解(noninferior solution):在多目标优化问题的可行域中存在一个问题解,若不存在另一个可行解,使得一个解中的目标全部劣于该解,则该解称为多目标优化问题的非劣解。所有非劣解的集合叫做非劣解集(noninferior set)。在求解实际问题中,过多的非劣解是无法直接应用的,决策者只能选择其中最满意的一个非劣解作为最终解。最终解主要有三种方法,第一种是求非劣解的生成法,包括加权法、约束法、加权法和约束法结合的混合法以及多目标遗传算法,即先求出大量的非劣解,构成非劣解的一个子集,然后按照决策者的意图找出最终解。第二种为交互法,主要为求解线性约束多目标优化的Geoffrion法,不先求出很多的非劣解,而是通过分析者与决策者对话的方式,逐步求出最终解。第三种是事先要求决策者提供目标之间的相对重要程度,算法以此为依据,将多目标问题转化为单目标问题进行求解。
利用进化算法求解多目标优化问题是近年来的研究热点,1967年,Rosenberg就建议采用基于进化的搜索来处理多目标优化问题,但没有具体实现。1975年,Holland提出了遗传算法,10年后,Schaffer提出了矢量评价遗传算法,第一次实现了遗传算法与多目标优化问题的结合。1989年,Goldberg在其著作《Genetic Algorithms for Search, Optimization, and Machine Learning》中,提出了把经济学中的Pareto理论与进化算法结合来求解多目标优化问题的新思路,对于后续进化多目标优化算法的研究具有重要的指导意义。目前,采用多目标进化算法求解多目标问题已成为进化计算领域中的一个热门方向,粒子群优化、蚁群算法、人工免疫系统、分布估计算法、协同进化算法、进化算法等一些新的进化算法陆续被用于求解多目标优化问题。本案例采用多目标粒子群算法求解多目标背包问题。
2 案例背景
2.1 问题描述
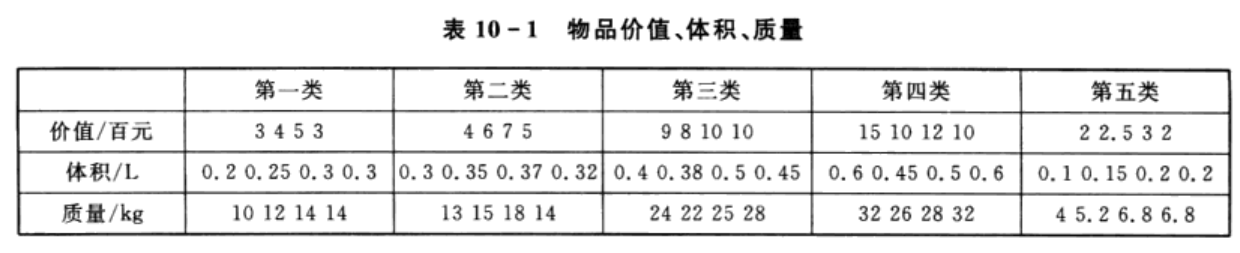
假设存在五类物品,每类物品中又包含四种具体物品,现要求从这五种类别物品中分别选择一种物品放入背包中,使得背包内物品的总价值最大,总体积最小,并且背包的总质量不超过92 kg。背包问题的数学模型为


2.2 算法流程
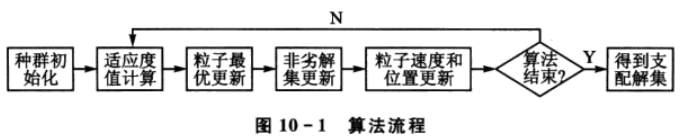
基于粒子群算法的二维多目标搜索算法流程如图10-1所示。其中,种群初始化模块随机初始化粒子的位置x和速度v,适应度值计算是指根据适应度值计算公式计算个体适应度值,粒子最优更新模块根据新的粒子位置更新个体最优粒子。非劣解集更新模块根据新粒子支配关系筛选非劣解。粒子速度和位置更新模块根据个体最优粒子位置和全局粒子位置更新粒子速度和位置。
2.3 适应度计算
粒子适应度值参考式(10-1),每个个体的适应度值有两个,即价值和体积,同时个体须满足质量约束。
2.4 筛选非劣解集
筛选非劣解集主要分为初始筛选非劣解集和更新非劣解集。初始筛选非劣解集是指在粒子初始化后,当一个粒子不受其他粒子支配(即不存在其他粒子的Px,Rx,均优于该粒子)时,把粒子放入非劣解集中,并且在粒子更新前从非劣解集中随机选择一个粒子作为群体最优粒子。更新非劣解集是指当新粒子不受其他粒子以及当前非劣解集中粒子的支配时,把新粒子放入非劣解集中,并且每次粒子更新前都从非劣解集中随机选择一个粒子作为群体最优粒子。
2.5 粒子速度和位置更新
粒子更新公式如下:
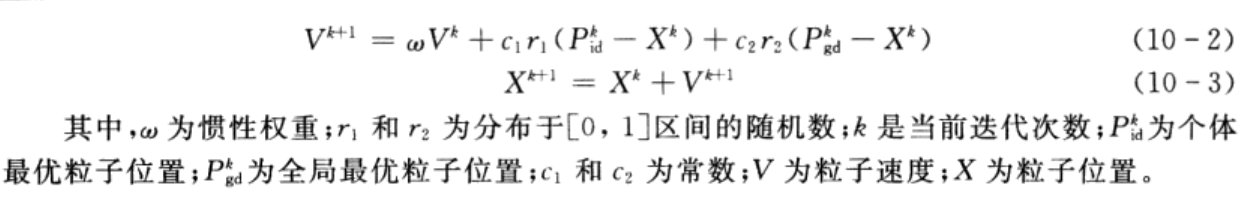
2.6 粒子最优
粒子最优包括个体最优粒子和群体最优粒子,其中个体最优粒子的更新方式是从当前新粒子和个体最优粒子中选择支配粒子,当两个粒子都不是支配粒子时,从中随机选择一个粒子作为个体最优粒子。群体最优粒子为从非劣解集中随机选择的一个粒子。
3 MATLAB程序实现
根据多目标搜索算法原理,在MATLAB中实现基于粒子群算法的多目标搜索算法。
%% 该函数演示多目标perota优化问题
%清空环境
clc
clear
load data
%% 初始参数
objnum=size(P,1); %类中物品个数
weight=92; %总重量限制
%初始化程序
Dim=5; %粒子维数
xSize=50; %种群个数
MaxIt=200; %迭代次数
c1=0.8; %算法参数
c2=0.8; %算法参数
wmax=1.2; %惯性因子
wmin=0.1; %惯性因子
x=unidrnd(4,xSize,Dim); %粒子初始化
v=zeros(xSize,Dim); %速度初始化
xbest=x; %个体最佳值
gbest=x(1,:); %粒子群最佳位置
% 粒子适应度值
px=zeros(1,xSize); %粒子价值目标
rx=zeros(1,xSize); %粒子体积目标
cx=zeros(1,xSize); %重量约束
% 最优值初始化
pxbest=zeros(1,xSize); %粒子最优价值目标
rxbest=zeros(1,xSize); %粒子最优体积目标
cxbest=zeros(1,xSize); %记录重量,以求约束
% 上一次的值
pxPrior=zeros(1,xSize);%粒子价值目标
rxPrior=zeros(1,xSize);%粒子体积目标
cxPrior=zeros(1,xSize);%记录重量,以求约束
%计算初始目标向量
for i=1:xSize
for j=1:Dim %控制类别
px(i) = px(i)+P(x(i,j),j); %粒子价值
rx(i) = rx(i)+R(x(i,j),j); %粒子体积
cx(i) = cx(i)+C(x(i,j),j); %粒子重量
end
end
% 粒子最优位置
pxbest=px;rxbest=rx;cxbest=cx;
%% 初始筛选非劣解
flj=[];
fljx=[];
fljNum=0;
%两个实数相等精度
tol=1e-7;
for i=1:xSize
flag=0; %支配标志
for j=1:xSize
if j~=i
if ((px(i)<px(j)) && (rx(i)>rx(j))) ||((abs(px(i)-px(j))<tol)...
&& (rx(i)>rx(j)))||((px(i)<px(j)) && (abs(rx(i)-rx(j))<tol)) || (cx(i)>weight)
flag=1;
break;
end
end
end
%判断有无被支配
if flag==0
fljNum=fljNum+1;
% 记录非劣解
flj(fljNum,1)=px(i);flj(fljNum,2)=rx(i);flj(fljNum,3)=cx(i);
% 非劣解位置
fljx(fljNum,:)=x(i,:);
end
end
%% 循环迭代
for iter=1:MaxIt
% 权值更新
w=wmax-(wmax-wmin)*iter/MaxIt;
%从非劣解中选择粒子作为全局最优解
s=size(fljx,1);
index=randi(s,1,1);
gbest=fljx(index,:);
%% 群体更新
for i=1:xSize
%速度更新
v(i,:)=w*v(i,:)+c1*rand(1,1)*(xbest(i,:)-x(i,:))+c2*rand(1,1)*(gbest-x(i,:));
%位置更新
x(i,:)=x(i,:)+v(i,:);
x(i,:) = rem(x(i,:),objnum)/double(objnum);
index1=find(x(i,:)<=0);
if ~isempty(index1)
x(i,index1)=rand(size(index1));
end
x(i,:)=ceil(4*x(i,:));
end
%% 计算个体适应度
pxPrior(:)=0;
rxPrior(:)=0;
cxPrior(:)=0;
for i=1:xSize
for j=1:Dim %控制类别
pxPrior(i) = pxPrior(i)+P(x(i,j),j); %计算粒子i 价值
rxPrior(i) = rxPrior(i)+R(x(i,j),j); %计算粒子i 体积
cxPrior(i) = cxPrior(i)+C(x(i,j),j); %计算粒子i 重量
end
end
%% 更新粒子历史最佳
for i=1:xSize
%现在的支配原有的,替代原有的
if ((px(i)<pxPrior(i)) && (rx(i)>rxPrior(i))) ||((abs(px(i)-pxPrior(i))<tol)...
&& (rx(i)>rxPrior(i)))||((px(i)<pxPrior(i)) && (abs(rx(i)-rxPrior(i))<tol)) || (cx(i)>weight)
xbest(i,:)=x(i,:);%没有记录目标值
pxbest(i)=pxPrior(i);rxbest(i)=rxPrior(i);cxbest(i)=cxPrior(i);
end
%彼此不受支配,随机决定
if ~( ((px(i)<pxPrior(i)) && (rx(i)>rxPrior(i))) ||((abs(px(i)-pxPrior(i))<tol)...
&& (rx(i)>rxPrior(i)))||((px(i)<pxPrior(i)) && (abs(rx(i)-rxPrior(i))<tol)) || (cx(i)>weight) )...
&& ~( ((pxPrior(i)<px(i)) && (rxPrior(i)>rx(i))) ||((abs(pxPrior(i)-px(i))<tol) && (rxPrior(i)>rx(i)))...
||((pxPrior(i)<px(i)) && (abs(rxPrior(i)-rx(i))<tol)) || (cxPrior(i)>weight) )
if rand(1,1)<0.5
xbest(i,:)=x(i,:);
pxbest(i)=pxPrior(i);rxbest(i)=rxPrior(i);cxbest(i)=cxPrior(i);
end
end
end
%% 更新非劣解集合
px=pxPrior;
rx=rxPrior;
cx=cxPrior;
%更新升级非劣解集合
s=size(flj,1);%目前非劣解集合中元素个数
%先将非劣解集合和xbest合并
pppx=zeros(1,s+xSize);
rrrx=zeros(1,s+xSize);
cccx=zeros(1,s+xSize);
pppx(1:xSize)=pxbest;pppx(xSize+1:end)=flj(:,1)';
rrrx(1:xSize)=rxbest;rrrx(xSize+1:end)=flj(:,2)';
cccx(1:xSize)=cxbest;cccx(xSize+1:end)=flj(:,3)';
xxbest=zeros(s+xSize,Dim);
xxbest(1:xSize,:)=xbest;
xxbest(xSize+1:end,:)=fljx;
%筛选非劣解
flj=[];
fljx=[];
k=0;
tol=1e-7;
for i=1:xSize+s
flag=0;%没有被支配
%判断该点是否非劣
for j=1:xSize+s
if j~=i
if ((pppx(i)<pppx(j)) && (rrrx(i)>rrrx(j))) ||((abs(pppx(i)-pppx(j))<tol) ...
&& (rrrx(i)>rrrx(j)))||((pppx(i)<pppx(j)) && (abs(rrrx(i)-rrrx(j))<tol)) ...
|| (cccx(i)>weight) %有一次被支配
flag=1;
break;
end
end
end
%判断有无被支配
if flag==0
k=k+1;
flj(k,1)=pppx(i);flj(k,2)=rrrx(i);flj(k,3)=cccx(i);%记录非劣解
fljx(k,:)=xxbest(i,:);%非劣解位置
end
end
%去掉重复粒子
repflag=0; %重复标志
k=1; %不同非劣解粒子数
flj2=[]; %存储不同非劣解
fljx2=[]; %存储不同非劣解粒子位置
flj2(k,:)=flj(1,:);
fljx2(k,:)=fljx(1,:);
for j=2:size(flj,1)
repflag=0; %重复标志
for i=1:size(flj2,1)
result=(fljx(j,:)==fljx2(i,:));
if length(find(result==1))==Dim
repflag=1;%有重复
end
end
%粒子不同,存储
if repflag==0
k=k+1;
flj2(k,:)=flj(j,:);
fljx2(k,:)=fljx(j,:);
end
end
%非劣解更新
flj=flj2;
fljx=fljx2;
end
%绘制非劣解分布
plot(flj(:,1),flj(:,2),'o')
xlabel('P')
ylabel('R')
title('最终非劣解在目标空间分布')
disp('非劣解flj中三列依次为P,R,C')3.1 仿真结果
本案例问题中,每类物品的价值、体积和质量如表10-1所列。

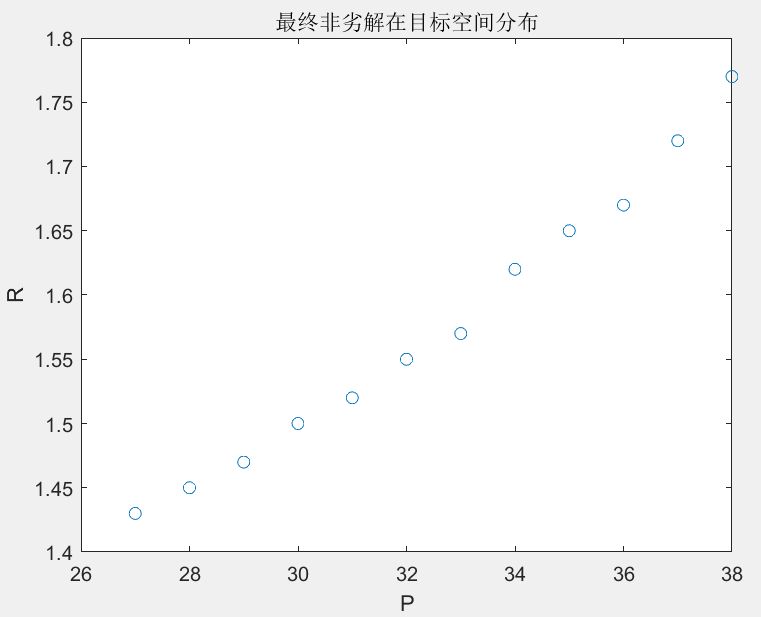
从每类物品中选择一个物品放入背包,使背包的总价值最大,体积最小,并且背包总质量小于92kg。粒子群算法参数为:粒子个数为50,迭代次数为200,最终得到的非劣解在目标空间中的分布如图10-2所示。

由图10-2可知,算法搜索到的非劣解构成了Pareto面,算法搜索取得了很好的效果。
4 延伸阅读
多目标搜索算法相对于单目标算法来说,更加贴近于实际问题,求解结果更具有参考价值。通过多目标搜索算法最终得到的不是一个最优解,而是一个非劣解集,需要从非劣解集中根据实际问题的需要选择一个解作为该问题的最终解。常用的基于进化算法的多目标搜索算法除了本案例介绍的方法之外,还有基于遗传算法的多目标搜索算法、基于免疫算法的多目标搜索算法等。