一、引言
全息技术作为一种新的成像技术近年来得到迅速的发展，计算机制全息图不需要实物的存在，同时还能通过计算机实现像的再现。计算全息图主要包括迂回位相型计算全息图和修正离轴参考光计算全息图，这两类全息图由不同的编码方式得到。前者直接编码光波的复振幅，用透明孔的大小和位置分别记录振幅和相位，透过率非0即1；后者通过计算机加偏置分量使复振幅变为非复函数， 用灰度标志透过率大小。通过对比这两种方法，可以看出它们各自的特点和优势，还可以进一步优化精简程序，提高程序运行速度和再现像的质量 [1] 。
二、博奇编码原理
对于当前的显示装置，其输入只能是非负实值。然而，计算全息面记录的光场分布为存在振幅和相位信息的复值函数，需要把复值函数进行转换编码。常用的编码技术有迂回相位型编码和修正离轴型编码，后者如博奇编码 [2] 。
博奇编码是通过对全息面光波复振幅中的振幅信息进行编码。假设记录介质平面的物光波与平面参考光波分别为：
物光与参考光振幅分别用A(x, y)、R表示；相位分别用jφ(x, y)、j2παx表示，其中α=sinθ/λ，表示参考光的空间频率。
因此记录平面的光强分布由物光与参考光干涉得到：
可以看出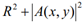
为零级衍射光信息的偏置分量，这种偏置分量使得 h(x, y)为正实值函数，不仅与物体再现信息无关，而且占用信道，提高了带宽；
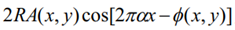则提供了物体全部的信息。由此，可以通过其他形式的偏置分量降低带宽，减少抽样点，制作具有高质量再现像的全息图。
博奇编码通过引入常数项代替原来的偏置分量，对物光波A(x, y)归一化得到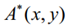 
，并使R=1，从而构成新的全息函数：
三、Matlab再现
本博文对博奇编码计算全息图进行了复现，图1为博奇编码后的全息图及再现图，图(a)为分辨率为256×256的原始图，图(b)为博奇编码的全息图，图©为再现图。博奇编码只对振幅进行编码，有效减少了空间带宽积，能得到很好的重建结果。
四、全息再现实验系统
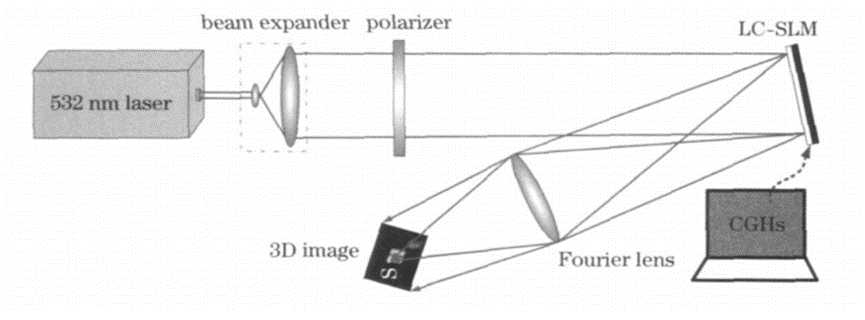
将各编码好的计算全息图或相息图加载到如图2所示的基于相位型液晶空间光调制器的全息再现系统，即可获得再现像。
五、参考文献
[1] 尹杰茜, 黄水平. 迂回位相型计算全息图和修正离轴参考光计算全息图的对比讨论[J]. 大学物理实验, 2015, 28(02): 6-10.
[2] 王冰洋. 多视投影计算全息图生成方法研究[D]: 桂林电子科技大学, 2019.
[3] 郑华东, 代林茂, 王涛, et al. 三维物场多重分数傅里叶变换全息图光电再现实验研究[J]. 激光与光电子学进展, 2011, 48(02): 22-27.
六、Matlab程序开发与实验指导
博主在读博士期间开展过全息三维显示相关实验，相关matlab程序开发、实验指导，请私信博主。
⭐️◎⭐️◎⭐️◎⭐️ · · · **博 主 简 介** · · · ⭐️◎⭐️◎⭐️◎⭐️ ♪▁▂▃▅▆▇ 博士研究生生 ，研究方向主要涉及定量相位成像领域，具体包括干涉相位成像技术(如**全息干涉☑**、散斑干涉☑等)、非干涉法相位成像技术(如波前传感技术☑，相位恢复技术☑)、此外，还对各种相位解包裹算法☑，相干噪声去除算法☑等开展过深入的研究。
