位图

概念：就是用每一位来存放某种状态，适用于海量数据，数据无重复的场景。通常是用来判断某个数据存不存在的。

比如，需要在40亿个整数中，查看某个数是否存在？

1G=1024M*1024KB*1024B~10亿字节~80亿比特。也就是说，存放40亿个整数需要开0.5G的内存（40亿个比特位）。每一个比特位代表着具体数字是否存在。

如下图：

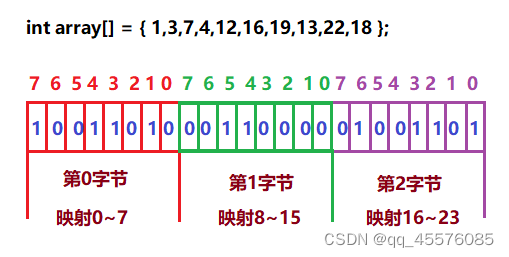
位图的实现如下：

#pragma once

namespace hzp {
	template<size_t N>
	class BitSet {
	public:
		BitSet() {
			_bits.resize(N / 8 + 1, 0);
		}
		void set(size_t x) {//将对应比特位x置为1
			size_t i = x / 8;//在第i个字节上
			size_t j = x % 8;//在第j个比特位上
			_bits[i] |= (1 << j);
		}
		void reset(size_t x) {//将对应比特位x置为0
			size_t i = x / 8;//在第i个字节上
			size_t j = x % 8;//在第j个比特位上
			_bits[i] &= (~(1 << j));
		}
		bool test(size_t x) {//检测对应比特位x的数值
			size_t i = x / 8;//在第i个字节上
			size_t j = x % 8;//在第j个比特位上
			return _bits[i] & (1 << j);
		}
	private:
		vector<char> _bits;
	};
	void test_BitSet() {
		BitSet<100> bs;
		bs.set(5);
		bs.set(4);
		bs.set(10);
		bs.set(20);

		cout << bs.test(5) << endl;
		cout << bs.test(10) << endl;
		cout << bs.test(20) << endl;
		cout << bs.test(4) << endl << endl;

		bs.reset(5);
		bs.reset(10);
		bs.reset(20);

		cout << bs.test(5) << endl;
		cout << bs.test(10) << endl;
		cout << bs.test(20) << endl;
		cout << bs.test(4) << endl;
	}
}

 

位图的应用： 

1. 快速查找某个数据是否在一个集合中

2. 排序 + 去重

3. 求两个集合的交集、并集等

4. 操作系统中磁盘块标记（如Linux文件系统中的inode和data block映射）

布隆过滤器

位图的优势：节省空间，效率高。局限性：只能处理整数。

当我们需要处理字符串或者自定义类型的对象的时候，位图便不能满足我们的需求，这时就需要布隆过滤器

布隆过滤器利用hashfunc函数将字符串或自定义类型对象转换成整形，这个时候就能复用位图检查这些非整形对象是否存在了。但是，利用单个hashfunc函数处理字符串或其他类型的时候，可能会导致误判，比如处理“ate” “eat”的时候就可能导致误判。于是布隆过滤器采用多个hashfunc函数映射多个位置，以来降低误判率的方式处理误判。

布隆过滤器的查找：布隆过滤器的思想是将一个元素用多个哈希函数映射到一个位图中，因此被映射到的位置的比特 位一定为1。所以可以按照以下方式进行查找：分别计算每个哈希值对应的比特位置存储的是否为 零，只要有一个为零，代表该元素一定不在哈希表中，否则可能在哈希表中。 注意：布隆过滤器如果说某个元素不存在时，该元素一定不存在，如果该元素存在时，该元素可 能存在，因为有些哈希函数存在一定的误判。

另外一个问题就是，我们需要开多少位的问题？这里给出下面的公式：

​​​​​​​ 

当我们的布隆过滤器的hashfunc函数的个数为三的时候，存在插入元素个数和布隆过滤器的以下关系：4.2*n=m 

布隆过滤器的实现如下：

#pragma once
#include "BitSet.h"

struct BKDRHash {
	size_t operator()(const string& s) {
		//BKDR
		size_t value = 0;
		for (auto& e : s) {
			value *= 31;
			value += e;
		}
		return value;
	}
};
struct APHash {
	size_t operator()(const string& s) {
		size_t hash = 0;
		for (long i = 0; i < s.size(); i++) {
			if ((i & 1) == 0) {
				hash ^= ((hash << 7) ^ s[i] ^ (hash >> 3));
			}
			else {
				hash ^= (~((hash << 11) ^ s[i] ^ (hash >> 5)));
			}
		}
		return hash;
	}
};
struct DJBHash {
	size_t operator()(const string& s) {
		size_t hash = 5381;
		for (auto ch : s) {
			hash += (hash << 5) + ch;
		}
		return hash;
	}
};
namespace hzp {
	template<size_t N, size_t X = 4, class K = string, 
		class HashFunc1 = BKDRHash, class HashFunc2 = APHash, class HashFunc3 = DJBHash>
	class BloomFilter {
	public:
		void Set(const K& key) {
			size_t len = X * N;
			size_t index1 = HashFunc1()(key) % len;
			size_t index2 = HashFunc2()(key) % len;
			size_t index3 = HashFunc3()(key) % len;

			_bs.set(index1);
			_bs.set(index2);
			_bs.set(index3);
		}

		bool Test(const K& key) {
			size_t len = X * N;
			size_t index1 = HashFunc1()(key) % len;
			if (_bs.test(index1) == false)
				return false;
			size_t index2 = HashFunc2()(key) % len;
			if (_bs.test(index2) == false)
				return false;
			size_t index3 = HashFunc3()(key) % len;
			if (_bs.test(index3) == false)
				return false;
			return true;
		}
	private:
		BitSet<X* N> _bs;
	};

	void test_bloomFilter() {
		BloomFilter<100> bf;
		bf.Set("沙僧");
		bf.Set("孙悟空");
		bf.Set("唐僧");
		bf.Set("猪八戒");

		cout << bf.Test("沙僧") << endl;
		cout << bf.Test("孙悟空") << endl;
		cout << bf.Test("唐僧") << endl;
		cout << bf.Test("猪八戒") << endl;
		cout << bf.Test("白骨精") << endl;
		cout << bf.Test("牛魔王") << endl;
		cout << bf.Test("红孩儿") << endl;
	}
}