图的概念和功能函数实现
- 前言
- 1.图的定义和术语
- 1.1 定义
- 1.2 常用术语
- 2.图的存储结构
- 2.1 图的数组(邻接矩阵)存储表示
- 2.2 图的邻接表存储表示
- 3.图的遍历
- 3.1 深度优先搜索
- 3.2 广度优先搜索
- 3.3 示例
- 4.连通网的最小生成树
- 4.1 克鲁斯卡尔(Kruskal)算法
- 4.2 普里姆(Prim)算法
- 5.图的建立及其接口函数的实现
- 结语
前言
图是一种比线性表和树更复杂的数据结构。在线性表中,数据元素之间仅有线性关系每个元素只有一个直接前驱和一个直接后继。在树形结构中,数据元素之间存在明显的层次关系,并且每层的元素可能和下一层的多个元素(即其孩子结点)相邻,但只能和上一层的个元素(即其双亲结点)相邻。而在图形结构中,结点之间的关系可以是任意的,图中任意两个元素之间都可能相邻。图的应用极为广泛,俗话说“千言万语不如一张图”,因此图是计拿机应用过程中对实际问题进行数学抽象和描述的强有力的工具。图论是专门研究图的性质的一个数学分支,在离散数学中占有极为重要的地位。图论注重研究图的纯数学性质,而数据结构中对图的讨论则侧重于在计算机中如何表示图以及如何实现图的操作和应用等。
1.图的定义和术语
1.1 定义
图(graph)由一个顶点(vertex)的有穷非空集 V(G)和一个弧(arc)的集合 E(G)组成通常记作 G-(V,E)。图中的顶点即为数据结构中的数据元素,孤的集合 E实际上是定义在顶点集合上的一个关系。以下用有序对(u,w)表示从到w 的一条弧(arc)。孤有方向性,需以一带箭头的线段表示,通常称 (没有箭头的出发端)为弧尾(tail)或始点(initianode),称w(带箭头的终止端)为弧头(head)或终点(terminal node),此时的图称为有向图(digraph)。若图中从 乙到w 有一条弧,同时从w到也有一条弧,则以无序对(v,w)代替这两个有序对(v,w)和(w,v),表示 v和w 之间的一条边。此时的图在顶点之间不再强调方向性的特征,称为无向图(undigraph)。
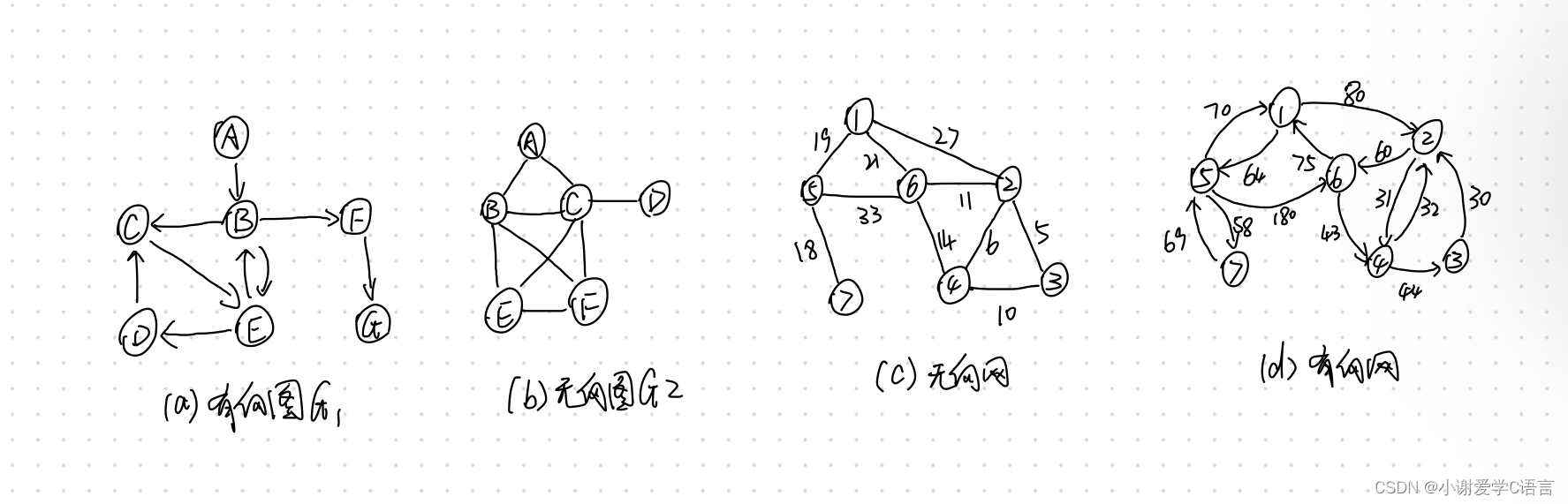
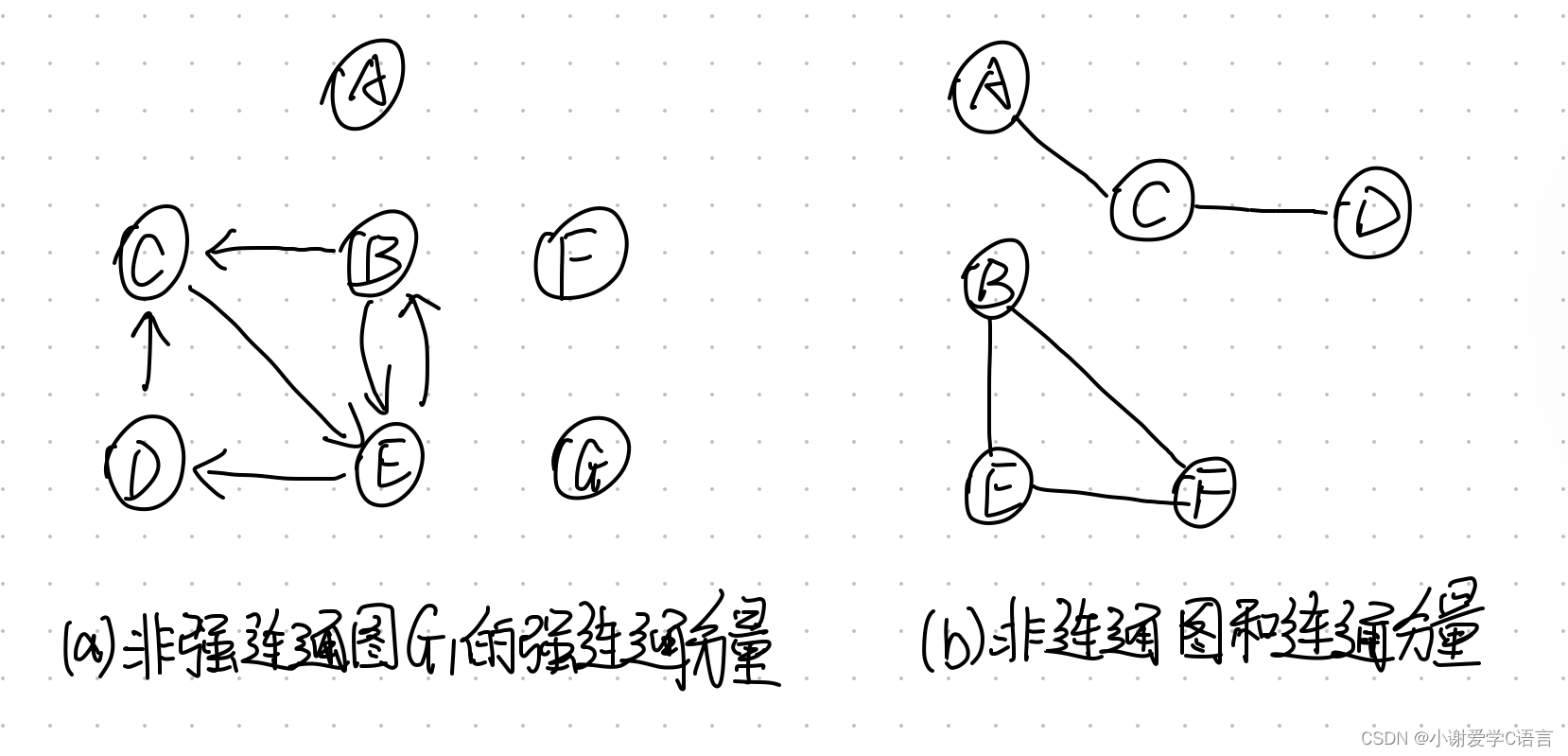
例如图(a)中的 G,是有向图G1=(V1,{A1})
其中:
V1={A,C,B,F,D,E,G}
A1={<A,B>,<B,C>,<B,F>,<B,E>,<C,E>,<E,D>,<D,C>,<E,B>,<F,G>}
图(b)中的 G2为无向图G2=(V2,{E2})
其中:
V2={A,B,C,D,E,F}
E ={(A,B),(A,C),(B,C),(B,E),(B,F),(C,F),(C,D),(E,F),(C,E)}
注意:有向图的边用<>,无向图的边用()
在实际应用中,图的弧或边往往与具有一定意义的数相关,称这些数为“权(weight)”。分别称带权的有向图和无向图为有向网(network)和无向网,如图©和(d)所示。
1.2 常用术语
稀疏图和稠密图
假设用 n 表示图中顶点数目,用 e 表示边或弧的数目。若不考虑顶点到其自身的弧或边,则对于无向图,边数 e 的取值范围是 0到 n(n-1)/2。称具有 n(n-1)/2条边的无向图为完全图(completed graph)。对于有向图,弧的数目 e的取值范围是到n(n-1)。称具有 n(n-1)条弧的有向图为有向完全图。若 e<nlogn,则称为稀疏图(sparse graph),反之称为稠密图(dense graph)。
子图
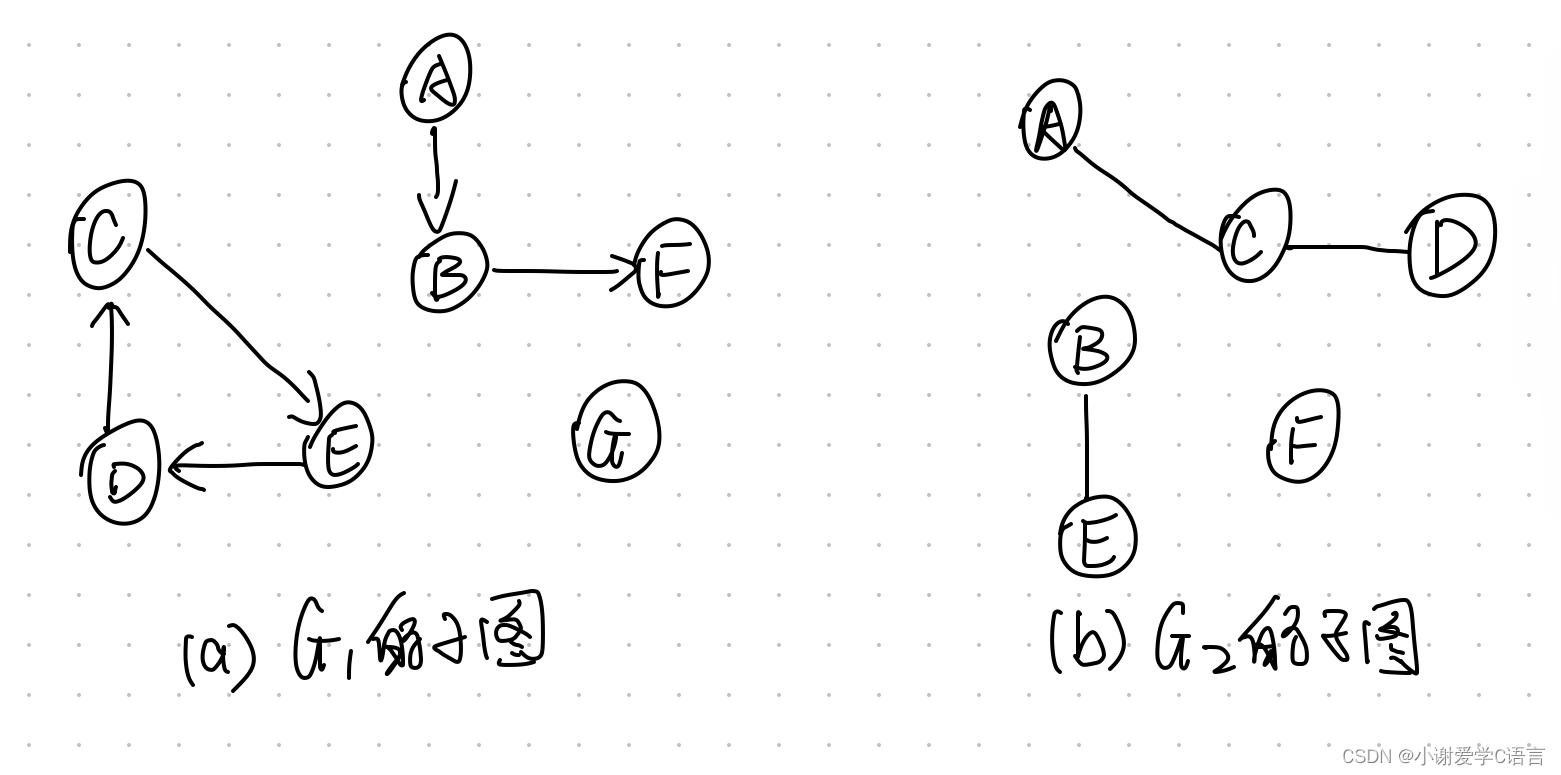
假设有两个图G=(V,{E})和G’=(V’,{E’})如果V’属于V且E’属于E,则称G’为G的子图(subgraph)。如下图
度、入度和出度
若 u一>v是图中一条弧,则称u邻接到v,或v邻接自u。图中所邻接到该顶点v的弧(即以它为弧头的弧)的数目,称为该顶点的入度(indegree),记作 ID(v);反之,从某顶点u出发的弧(即邻接自该顶点的弧)的数目,称为该顶点的出度(outdegree),记作 OD(u)。顶点 v的入度和出度之和称为该顶点的总度,简称为度(degree),记作 TD(v).例如,图G1中顶点 B的入度ID(B)=2,出度 OD(B)=3,度 TD(B)=5。无向图中顶点的度定义为与该顶点相连的边的数目。
路径和回路
若有向图G中k+1个顶点之间都有弧存在(即<v0,v1>,<v1,v2>,…<v(k-1),vk>是图G中的弧),则这个顶点的序列{v0,v1,v2,…,vk}为从顶点。到顶点v0到vk的一条有向路径,路径中弧的数目定义为路径长度。若序列中的顶点都不相同,则为简单路径。对无向图,相邻顶点之间存在边的k+1个顶点序列构成一条长度为k的无向路径。如果v0和vk是同一个顶点,则是一条由某个顶点出发又回到自身的路径,称这种路径为回路或环(cycle)。
连通图和连通分量
若无向图中任意两个顶点之间都存在一条无向路径,则称该无向图为连通图。对有向图而言,若图中任意两个顶点之间都存在一条有向路径,则称该有向图为强连通图。例如,图G2为连通图,图G1为非强连通图。非连通图中各个连通子图称为该图的连通分量。如图(b)为由两个连通分量构成的非连通图(a)所示为图G1的4个强连通分量。
2.图的存储结构
图是一种典型的复杂结约,图中顶点可能同任章一个其他的项点之间有关系。因此图没有顺序存储表示的结构。
2.1 图的数组(邻接矩阵)存储表示
邻接矩阵是用于描述图中顶点之间关系(及弧或边的权)的矩阵。
图G1和图G2的邻接矩阵分别如图(a)和(b)所示。由于一般情况下,图中都没有邻接到自身的弧;因此矩阵中的主对角线为全零。由于无向图中的一条边视为一对藏洲无向图的邻接矩阵必然是对称矩阵。网的邻接矩阵的定义中,当vi到vj有弧相邻接时;a i,j的值应为该弧上的权值否则为如图(d)所示为有向网的邻接矩阵。

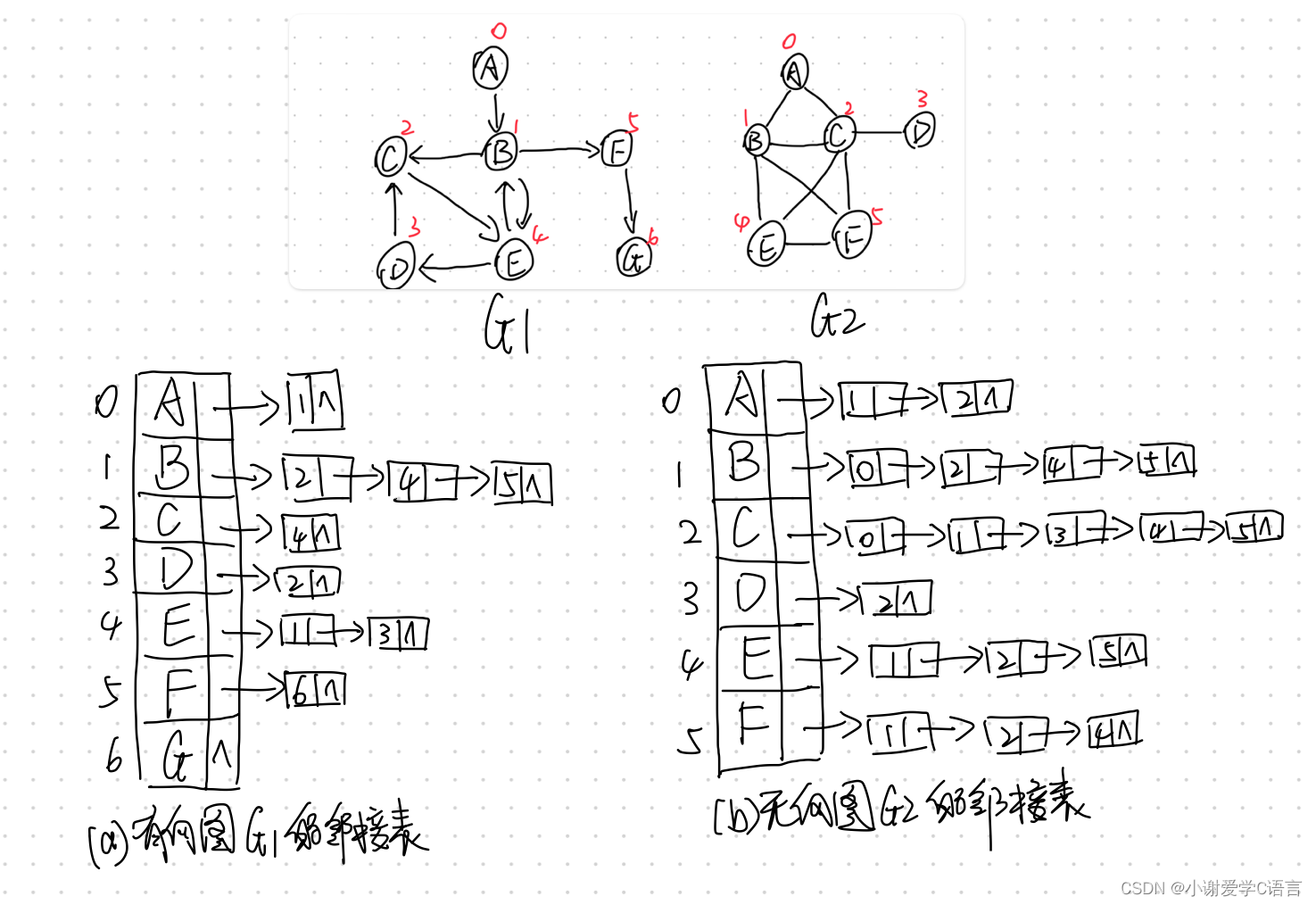
2.2 图的邻接表存储表示
邻接表(adjacency list)是图的一种链式存储表示方法,它类似于树的孩子链表。
从图中可见,在有向的邻接表中,从同一顶点出发的弧链接在同一链表中,邻接表中结点的个数恰为图中弧的数目,而在无向图的邻接表中,同一条边有两个结点,分别出现在和它相关的两个顶点的链表中,因此无向图的邻接表中结点个数是边数的两倍。在邻接表中,顶点表结点的排列次序决于建立图结构时输人信息的次序。
3.图的遍历
与二叉树和树的遍历类似,图结构也有遍历操作,即从某个顶点出发,沿着某条路径对图中其余顶点进行访问,且使每一个顶点只被访问一次。然而,图的遍历要比树的遍历复杂得多,因为在图中和同一顶点有弧或边相通的顶点之间也可能有弧或边,则在访问了某个而点之后,可能顺着某条回路又回到该顶点。例如图G2,由于图中存在回路,因此从而点A 出发,在访问了 B,C之后,又可以访问到顶点 A。为了避免同一顶点被重复访向多次,则在遍历过程中,必须为已经被访问过的顶点加上标识,以便再次途经这样的顶点时不再重访。为此,需附设一维数组 visited[o…n-1],令其每个分量对应图中一个顶点,各分量的初值均置为“FALSE”或“0”,一且访问了某个顶点,便将 visited 中相应分量的值置为“TRUE”或“被访问时的次序号”。通常,对图进行遍历可有两种搜索路径:深度优先搜索和广度优先搜索,以下分别讨论之。
3.1 深度优先搜索
深度优先搜索(depth first search)遍历类似于树的先根遍历,可以看成是树的先根遍历的推广。
假设初始状态是图中所有顶点均未被访问,则从某个顶点艺出发,首先访问该顶点,然后依次从它的各个未被访问的邻接点出发深度优先遍历图,直至图中所有和 有路径相的顶点都被访问到,若此时尚有其他顶点未被访问,则另选一个未被访问过的顶点作起始点,重复上述过程,直至图中所有顶点都被访问到为止。
显然,深度优先搜索是一个递归的过程。可将图的深度优先搜索遍历和树的先根遍历相比较,图中遍历的起始顶点对应于树的根结点,起始顶点的邻接点 wi对应于树根各孩子结点,从邻接点出发的遍历对应于从子树根出发的遍历,不同的是,树中各子树互不相交,因此对任一子树的遍历决不会访问到其他子树中的结点,而从图中某一邻接点 wi开始的遍历有可能访问到起始点的其他邻接点 wj,因此在图的遍历算法中必须强调“从各个未被访问的邻接点起进行遍历”。
3.2 广度优先搜索
广度优先搜索(breadth first search)的基本思想是:从图中某顶点v出发,在访问了v之后依次访问v的各个未曾访问过的邻接点,然后分别从这些邻接点出发依次访问它们的邻接点,并使得“先被访问的顶点的邻接点”先于“后被访问的顶点的邻接点”被访问,直至图中所有已被访问的顶点的邻接点都被访问到。如若此时图中尚有顶点未被访问,则需另选一个未曾被访问过的顶点作为新的起始点,重复上述过程,直至图中所有顶点都被访问到为止。换句话说,广度优先搜索遍历图的过程是以v为起始点,由近至远,依次访问和v有路径相通且路径长度为 1,2,…的顶点。
3.3 示例
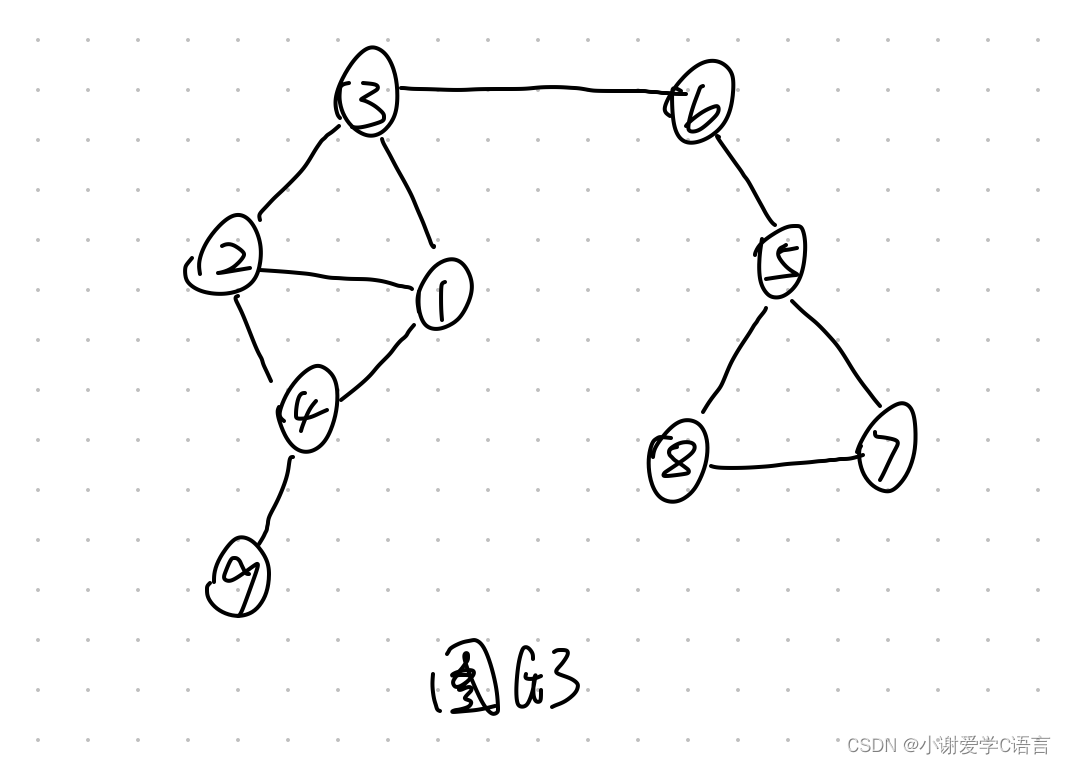
深度优先搜索
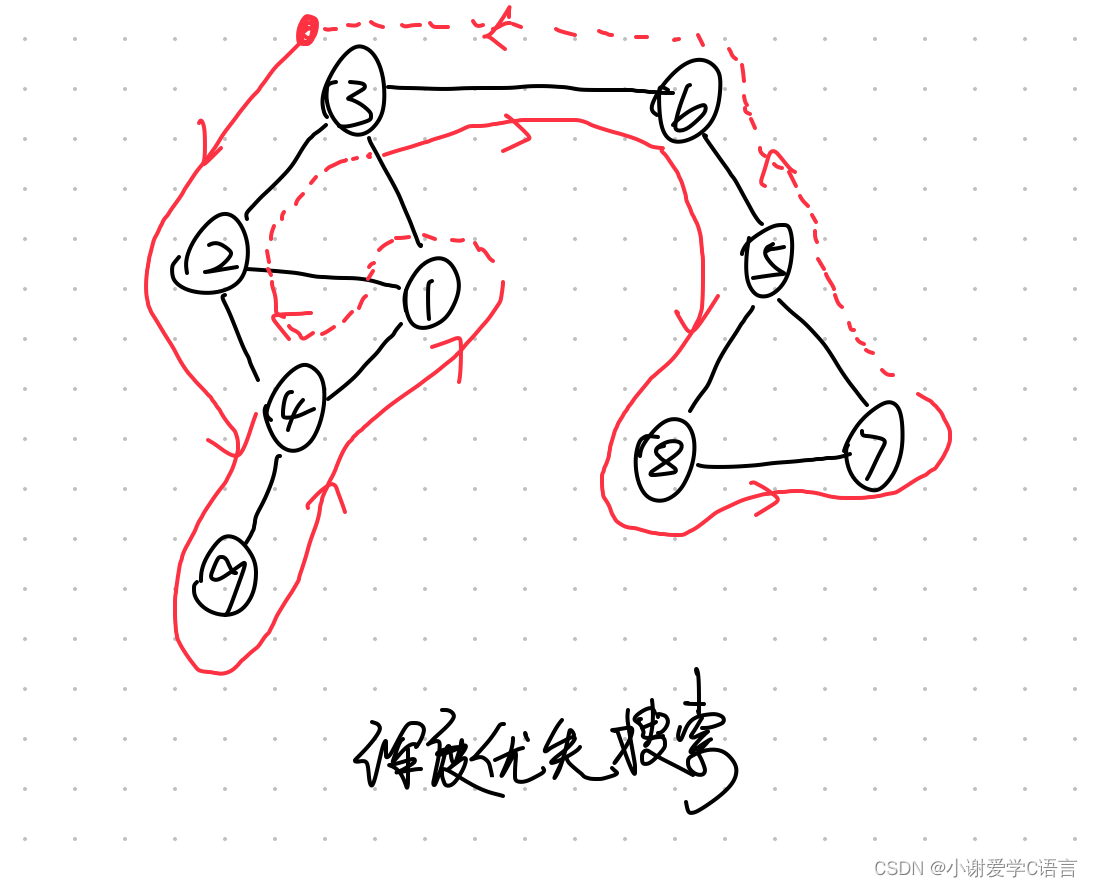
从v3开始遍历
顺序为:v3->v2->v4->v9->v1->v6->v5->v8->v7
广度优先搜索
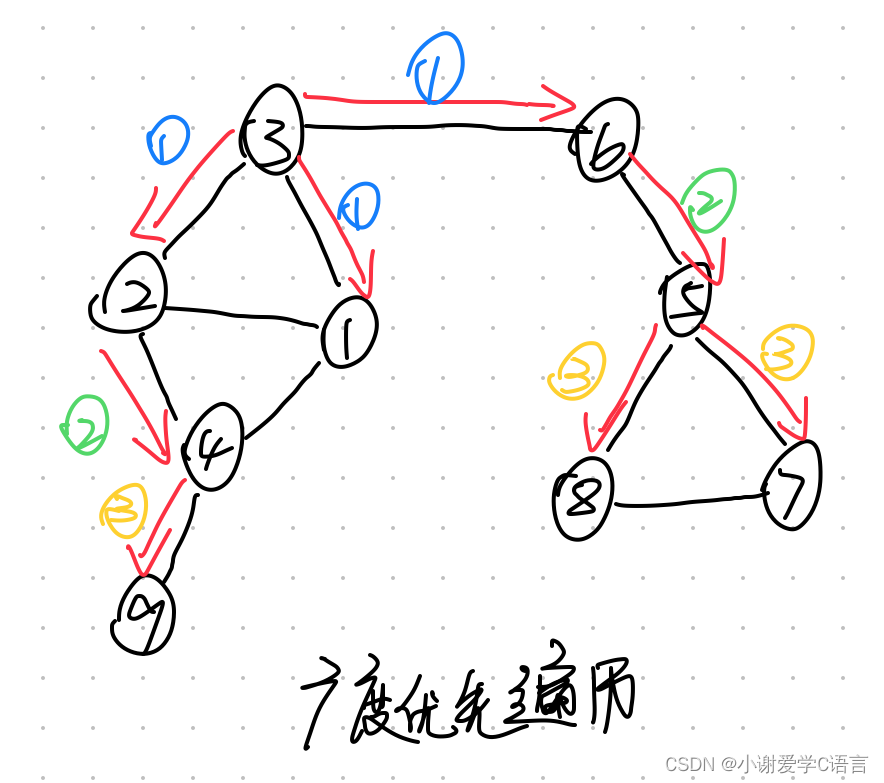
从v3开始遍历
顺序为:v3->v2->v1->v6->v4->v5->v9->v8->v7
4.连通网的最小生成树
在一个含有 n 个顶点的连通图中,必能从中选出n1条边构成一个极小连通子图,它含有图中全部 n 个顶点,但只有足以构成一棵树的 n-1条边,称这棵树为连通图的生成树。连通网的最小生成树则为权值和取最小的生成树。
如果用一个连通网表示 个居民点和各个居民点之间可能架设的通信线路,则网中每一条边上的权值可表示架设这条线路所需经费。由于在 个居民点间架构通信网只需架设n-1条线路,则工程队面临的问题是架设哪几条线路能使总的工程费用最低。这个问题等价于,在含有 n 个顶点的连通网中选择n一1条边,构成一棵极小连通子图,并使该连通子图中n-1条边上权值之和达到最小,则称这棵连通子图为连通网的最小生成树。
例如下图所示为连通网和它的三棵权值总和分别为 43、36 和 64 的生成树,其中以图©所示生成树的权值总和最小,且为图(a)中连通网的最小生成树。
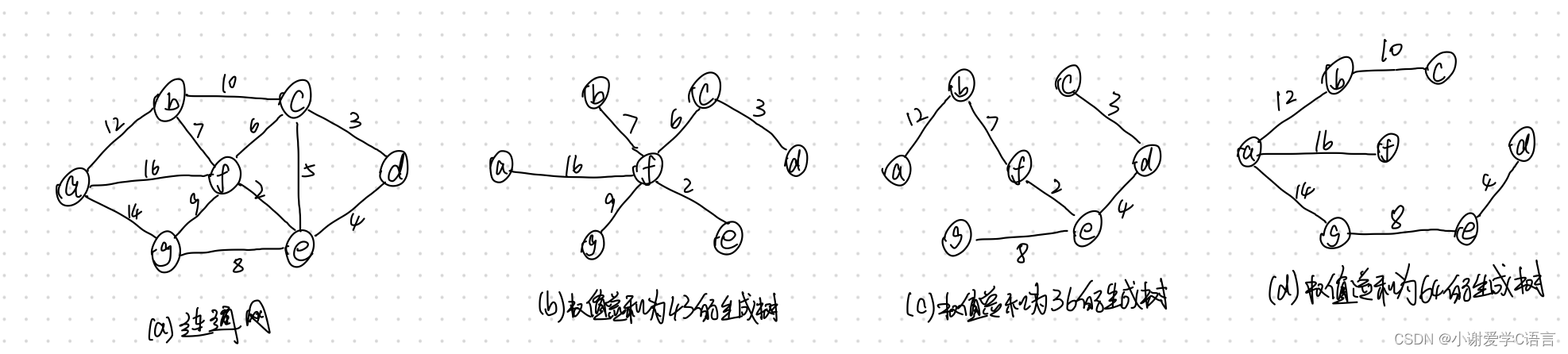
那么如何构造连通网的最小生成树?以下介绍求得最小生成树的两种算法:
4.1 克鲁斯卡尔(Kruskal)算法
克鲁斯卡尔算法的基本思想为:为使生成树上总的权值之和达到最小,应使每一条边上的权值尽可能小,自然应从权值最小的边选起,直至选出 #一1 条权值最小的边为止,然这n一1条边必须不构成回路。因此并非每一条居当前权值最小的边都可选。
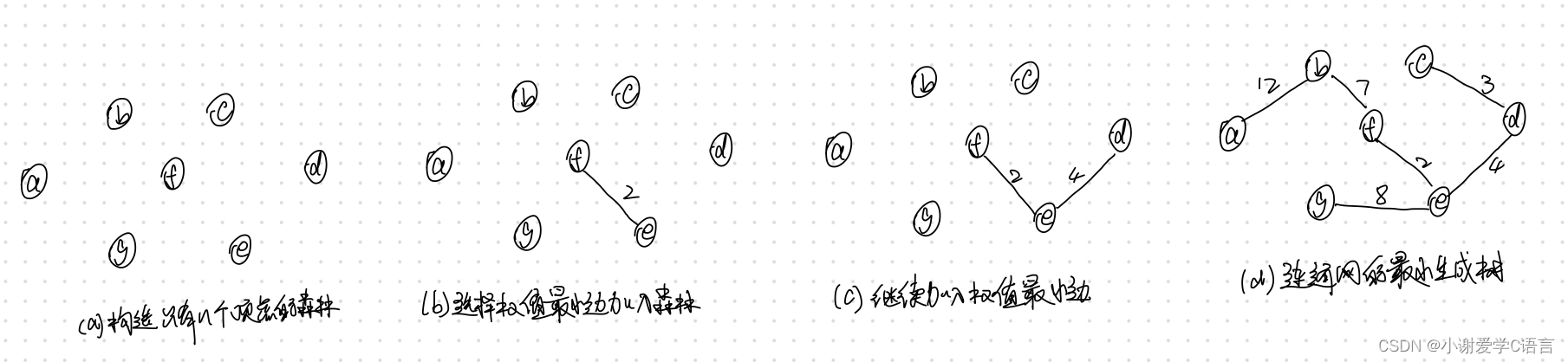
具体做法如下,首先构造一个只含n个顶点的森林,然后依权值从小到大从连通网中选择边加入到森林中去,并使森林中不产生回路,直至该森林变成一棵树为止。例如,对图(a)所示连通网按克鲁斯卡尔算法构造最小生成树的过程如图 7.12 所示,在选择权值最小(分别为 2、3 和4)的 3 条边之后,下一条权值最小的边是(c,e),但由于顶点c和e已在同一棵树上,加上边(c,e)将产生回路,因此不可取。同理权值为 6 的边(c,f)也不取。之后在选择了权值分别为7和8的边之后权值为10的边(b,c)也不可取,最后选择(a,b)。至此图中7个顶点都已落在同一棵树上,最小生成树构造完毕。从上述过程可见对上图(a)所示连通网,不可能再找到权值总和小于 36 的生成树了。
4.2 普里姆(Prim)算法
普里姆算法的基本思想是: 首先选取图中任意一个顶点v作为生成树的根,之后继续往生成树中添加顶点 w则在顶点 w 和顶点v之间必须有边,且该边上的权值应在所有和v相邻接的边中属最小。在一般情况下,从尚未落在生成树上的顶点中选取加入生成树的顶点应满足下列条件; 它和生成树上的顶点之间的边上的权值是在连接这两类顶点(一类是已落在生成树上的顶点,另一类是尚未落在生成树上的顶点)的所有边中权值属最小。例如对图(a)所示的连通网,假设从顶点 a 开始构建最小生成树。此时只有顶点 a 在生成树中,其余顶点 b、c、d、e、f、g 均不在生成树上。连接这两类顶点的边有(a,b)、(a,f)和(a,g),其中以边(a,b)的权值最小,则选择边(a,b)之后,顶点b加入到生成树中,之后在链接
(a,b)和{c,d,e,f,g)这两类顶点的边集{(b,c),(b,f),(a,f),(a,g)}中,选择权值最小(=7)的边(b,f)加人到生成树中,之后应在链接顶点(c,d,e,g)的边集{(b,c),(f,c),(f,e),(f,g),(a,g)}中选择权值最小的边(f,e)…,依此类推,直至所有顶点都落到生成树上为止。上述构筑生成树的过程如下图所示:
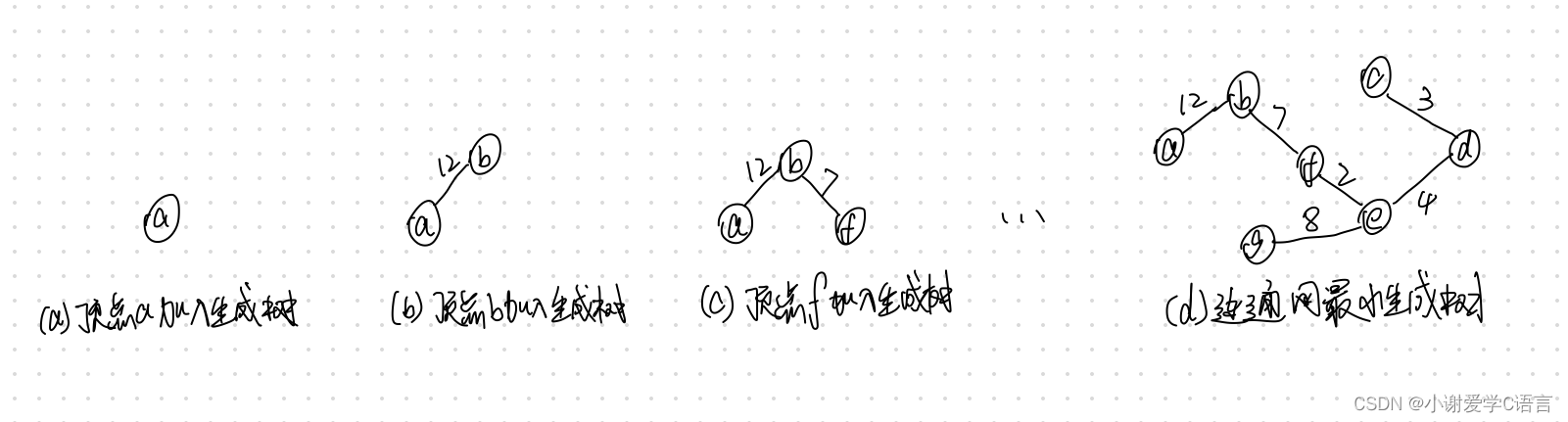
比较以上两个算法可见,克鲁斯卡尔算法主要对“边”进行操作,其时间复杂度为O(e),而普里姆算法主要对“顶点”进行操作,其时间复杂度为 O(n^2)。因此前者适于稀疏图,后适于稠密图。
5.图的建立及其接口函数的实现
代码如下:
#define _CRT_SECURE_NO_WARNINGS 1
#include <stdio.h>
#include <stdlib.h>
#define MAX_VERTICES 100
// 邻接表中的边节点
typedef struct EdgeNode {
int dest;//目标顶点
struct EdgeNode* next;//源顶点
} EdgeNode;
// 邻接表中的顶点节点
typedef struct VertexNode {
int data;//顶点值
EdgeNode* edges;//边值
int visited;//访问标记
} VertexNode;
// 图结构
typedef struct Graph {
VertexNode vertices[MAX_VERTICES];//顶点集合
int numVertices;//图中顶点下标数
} Graph;
// 初始化图
void initGraph(Graph* graph) {
graph->numVertices = 0;
for (int i = 0; i < MAX_VERTICES; i++) {
graph->vertices[i].data = 0;
graph->vertices[i].edges = NULL;
graph->vertices[i].visited = 0;
}
}
// 添加顶点
void addVertex(Graph* graph, int data) {
if (graph->numVertices < MAX_VERTICES) {
VertexNode* vertex = &(graph->vertices[graph->numVertices]);
vertex->data = data;
graph->numVertices++;
}
else {
printf("图已满,无法添加更多顶点\n");
}
}
// 添加边
void addEdge(Graph* graph, int src, int dest) {
if (src >= 0 && src < graph->numVertices && dest >= 0 && dest < graph->numVertices) {
EdgeNode* newEdge = (EdgeNode*)malloc(sizeof(EdgeNode));
newEdge->dest = dest;
newEdge->next = graph->vertices[src].edges;
graph->vertices[src].edges = newEdge;
}
else {
printf("顶点索引无效\n");
}
}
// 深度优先遍历递归函数
void dfsRecursive(Graph* graph, int vertex) {
printf("%d ", graph->vertices[vertex].data);
graph->vertices[vertex].visited = 1;
EdgeNode* edge = graph->vertices[vertex].edges;
while (edge != NULL) {
int dest = edge->dest;
if (!graph->vertices[dest].visited) {
dfsRecursive(graph, dest);
}
edge = edge->next;
}
}
// 深度优先遍历
void dfs(Graph* graph, int startVertex) {
for (int i = 0; i < graph->numVertices; i++) {
graph->vertices[i].visited = 0;
}
dfsRecursive(graph, startVertex);
}
// 广度优先遍历
void bfs(Graph* graph, int startVertex) {
int queue[MAX_VERTICES];
int front = 0;
int rear = 0;
for (int i = 0; i < graph->numVertices; i++) {
graph->vertices[i].visited = 0;
}
printf("%d ", graph->vertices[startVertex].data);
graph->vertices[startVertex].visited = 1;
queue[rear++] = startVertex;
while (front < rear) {
int vertex = queue[front++];
EdgeNode* edge = graph->vertices[vertex].edges;
while (edge != NULL) {
int dest = edge->dest;
if (!graph->vertices[dest].visited) {
printf("%d ", graph->vertices[dest].data);
graph->vertices[dest].visited = 1;
queue[rear++] = dest;
}
edge = edge->next;
}
}
}
int main() {
Graph graph;
initGraph(&graph);
int numVertices;
printf("输入图中的顶点数: ");
scanf("%d", &numVertices);
for (int i = 0; i < numVertices; i++) {
int data;
printf("输入顶点的值 %d: ", i);
scanf("%d", &data);
addVertex(&graph, data);
}
int numEdges;
printf("输入图中的边数: ");
scanf("%d", &numEdges);
for (int i = 0; i < numEdges; i++) {
int src, dest;
printf("输入边的源顶点和目标顶点 %d: ", i);
scanf("%d %d", &src, &dest);
addEdge(&graph, src, dest);
}
int startVertex;
printf("输入遍历的起始顶点: ");
scanf("%d", &startVertex);
printf("深度优先遍历: ");
dfs(&graph, startVertex);
printf("\n");
printf("广度优先遍历: ");
bfs(&graph, startVertex);
printf("\n");
return 0;
}
我们插入下面的一个简单的有向图
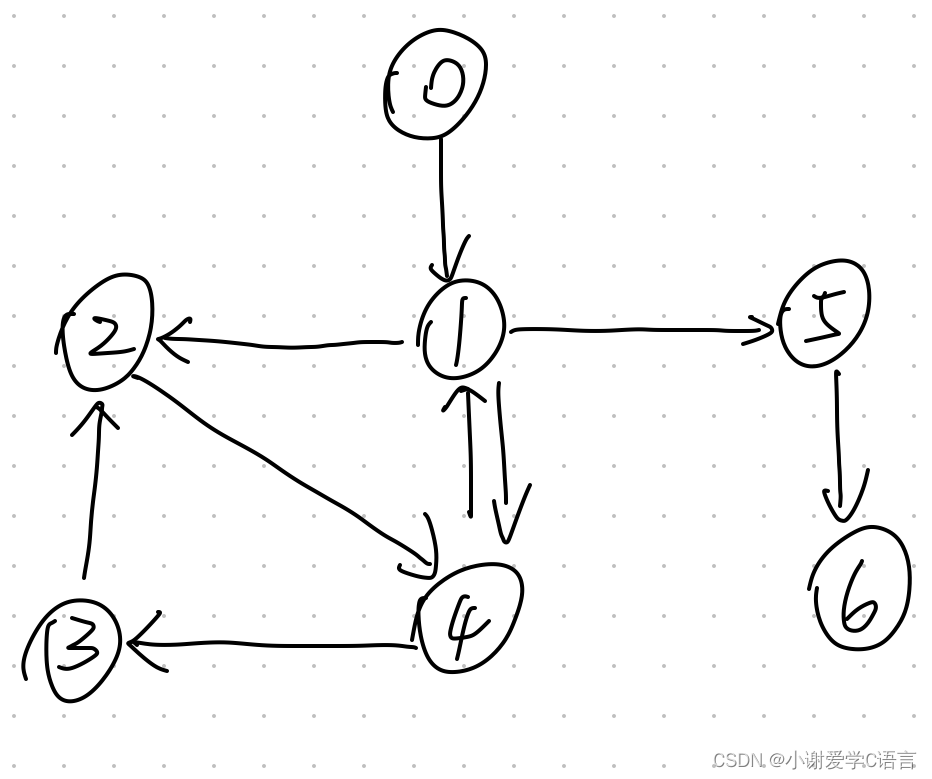
输出结果如下:
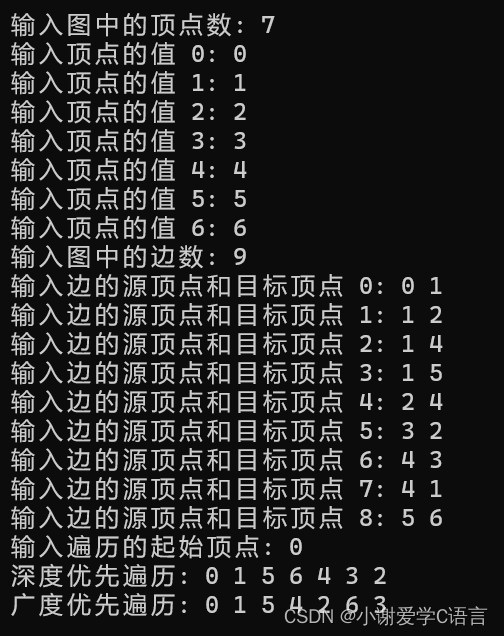
结语
这篇文章关于概念理论的介绍摘录自严蔚敏和陈文博的《数据结构及应用算法教程(修订版)》
有兴趣的小伙伴可以关注作者,如果觉得内容不错,请给个一键三连吧,蟹蟹你哟!!!
制作不易,如有不正之处敬请指出
感谢大家的来访,UU们的观看是我坚持下去的动力
在时间的催化剂下,让我们彼此都成为更优秀的人吧!!!