数据结构 --- 树

news2024/11/27 18:38:33

1、二叉树

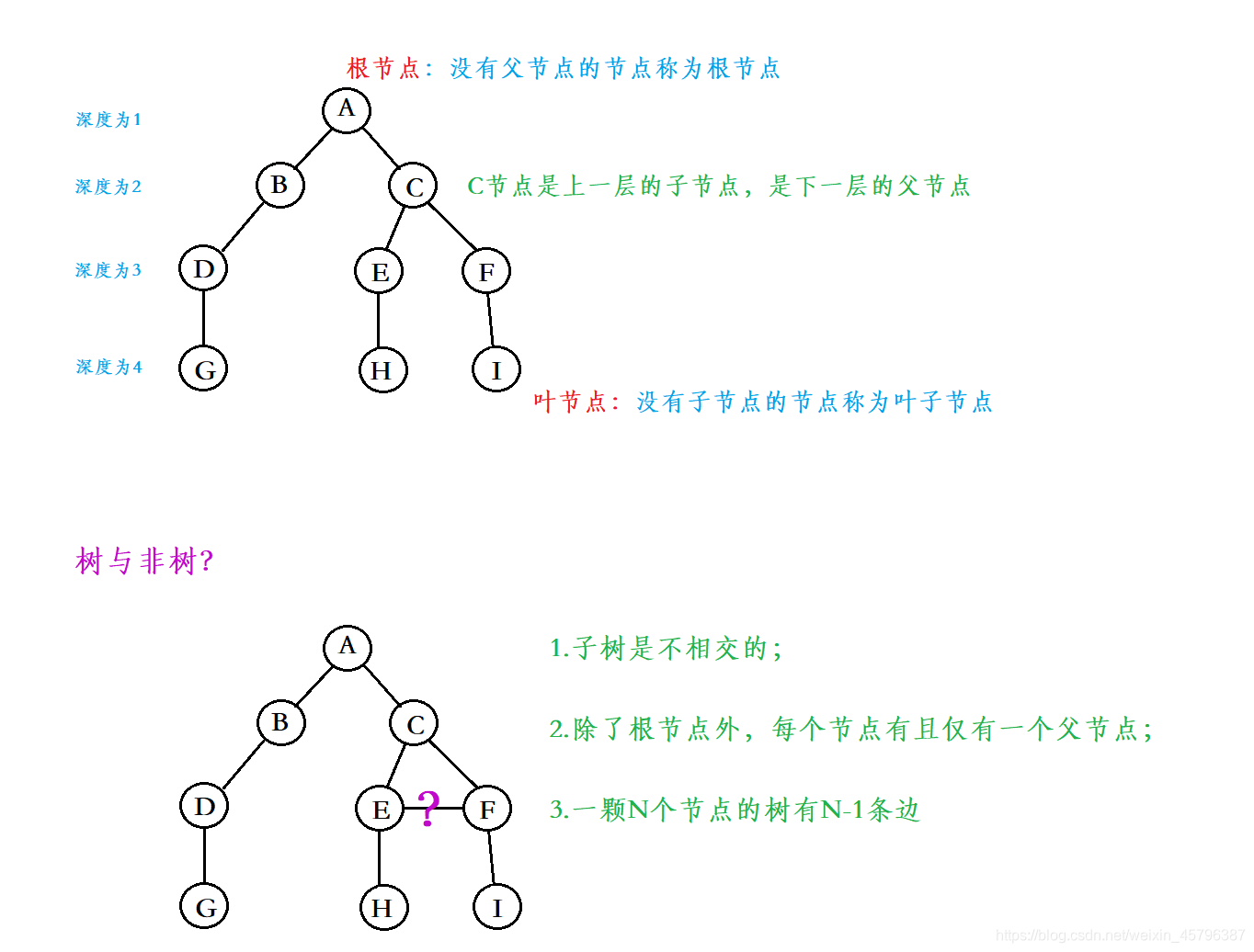
树是一种非线性的数据结构，它是由n（n>=0）个有限结点组成一个具有层次关系的集合。把它叫做树是因为它看起来像一棵倒挂的树，也就是说它是根朝上，而叶朝下的。

  1. 每个结点最多有两棵子树，即二叉树不存在度大于2的结点。
  2. 二叉树的子树有左右之分，其子树的次序不能颠倒。

在这里插入图片描述

 

2、 二叉树的遍历 --- 深度优先

深度优先可以分为以下三种

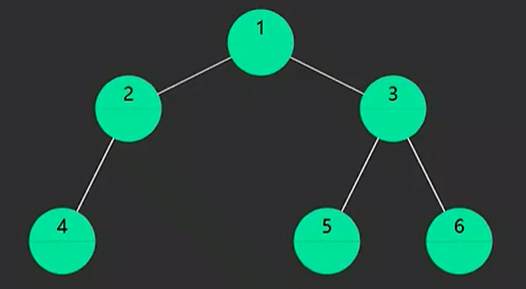
 1、前序遍历

规则：

  1. 先访问该节点
  2. 在访问左子树
  3. 在访问右子树

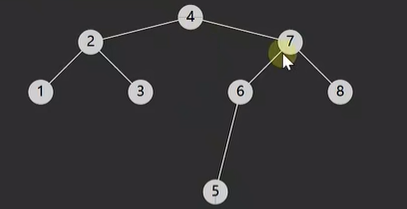
上述遍历顺序：1、2、4、3、5、6

    public void preOrder(TreeNode root) {
        // 递归结束条件
        if (root == null) {
            return;
        }
        // 当前节点
        System.out.println(root);

        // 左子树
        TreeNode left = root.left;
        preOrder(left);

        // 右子树
        TreeNode right = root.right;
        preOrder(right);
    }
    public void preOrder1(TreeNode root) {
        TreeNode curr = root;
        Stack<TreeNode> stack = new Stack<>();

        while (curr != null || stack.isEmpty()) {
            if (curr != null) {
                // 处理逻辑，处理当前节点
                System.out.println(curr); 
                // 利用栈，记录来的时候的顺序
                stack.push(curr);
                // 遍历左子树
                curr = curr.left;
            } else {
                // 从栈中弹出元素，遍历右子树
                TreeNode pop = stack.pop();
                curr = pop.right;
            }
        }
    }

2、中序遍历

 规则：

  1. 先访问左子树
  2. 在访问该节点
  3. 在访问右子树

上述遍历顺序：4、2、1、5、3、6

    public void inOrder(TreeNode root) {
        // 递归结束条件
        if (root == null) {
            return;
        }

        // 左子树
        TreeNode left = root.left;
        inOrder(left);

        // 当前节点
        System.out.println(root);

        // 右子树
        TreeNode right = root.right;
        inOrder(right);
    }
    public void inOrder1(TreeNode root) {
        TreeNode curr = root;
        Stack<TreeNode> stack = new Stack<>();

        while (curr != null || stack.isEmpty()) {
            if (curr != null) {
                // 利用栈，记录来的时候的顺序
                stack.push(curr);
                // 遍历左子树
                curr = curr.left;
            } else {
                // 处理逻辑，处理当前节点
                System.out.println(curr);
                // 从栈中弹出元素，遍历右子树
                TreeNode pop = stack.pop();
                curr = pop.right;
            }
        }
    }

3、后续遍历

 规则：

  1. 先访问左子树
  2. 在访问右子树
  3. 在访问该节点

上述遍历顺序：4、2、5、6、3、1

    public void postOrder(TreeNode root) {
        // 递归结束条件
        if (root == null) {
            return;
        }

        // 左子树
        TreeNode left = root.left;
        postOrder(left);

        // 右子树
        TreeNode right = root.right;
        postOrder(right);

        // 当前节点
        System.out.println(root);
    }
    public void postOrder1(TreeNode root) {
        TreeNode curr = root;
        Stack<TreeNode> stack = new Stack<>();
        TreeNode pop = null; // 记录最近一次弹出栈的元素
        while (curr != null || stack.isEmpty()) {
            if (curr != null) {
                // 利用栈，记录来的时候的顺序
                stack.push(curr);
                // 遍历左子树
                curr = curr.left;
            } else {
                // 从栈中弹出元素，遍历右子树
                TreeNode peek = stack.peek();
                // 判断栈顶元素的右子树是否处理，如果已经处理，就可以弹出栈
                if (peek.right == null || peek.right == pop) {
                    pop = stack.pop();
                    // 处理逻辑，处理当前节点
                    System.out.println(pop.val);
                } else {
                    curr = peek.right;
                }
            }
        }
    }

例题：

101. 对称二叉树

给你一个二叉树的根节点 root ， 检查它是否轴对称。

解题思路

  1. 轴对称，其实就是左右两边子树是否对称
  2. 从根节点开始，比较左子节点和右子节点是否相等
  3. 比较左子节点的左子节点和右子节点的右子节点是否相等
  4. 比较左子节点的左右子节点和右子节点的右左子节点是否相等

有点绕，需要慢慢体会。

class Solution {
    public boolean isSymmetric(TreeNode root) {
        if (root == null) {
            return true;
        }
        return check(root.left, root.right);

    }

    public boolean check(TreeNode left, TreeNode right) {
        if (left == null && right == null) {
            return true;
        }
        if (left == null || right == null) {
            return false;
        }
        if (left.val != right.val) {
            return false;
        }
        return check(left.left, right.right) && check(left.right, right.left);
    }
}

104. 二叉树的最大深度

给定一个二叉树，找出其最大深度。二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。

解题思路：

递归：

找到左子树的深度和右子树的深度较大的哪一个。然后加一。

class Solution {
    public int maxDepth(TreeNode root) {
        if(root==null){
            return 0;
        }else {
            int leftHeight=maxDepth(root.left);
            int rightHeight=maxDepth(root.right);
            return Math.max(leftHeight,rightHeight)+1;
        }
    }
}

BFS层序遍历

层序遍历，知道多少层，就知道最大深度了。

public class Test104 {
    public int maxDepth(TreeNode root) {
        if (root == null) {
            return 0;
        }
        Queue<TreeNode> queue = new ArrayDeque<>();
        queue.offer(root);
        int level = 0;
        while (!queue.isEmpty()) {
            int size = queue.size();
            for (int i = 0; i < size; i++) {
                TreeNode poll = queue.poll();
                if (poll.left != null) {
                    queue.offer(poll.left);
                }
                if (poll.right != null) {
                    queue.offer(poll.right);
                }
            }
            level++;
        }
        return level;
    }
}

111. 二叉树的最小深度

给定一个二叉树，找出其最小深度。最小深度是从根节点到最近叶子节点的最短路径上的节点数量。

解题1：

递归，但是要注意一点，如果左右子树为null的时候，就不应该计算进去。

    public int minDepth(TreeNode root) {
        if (root == null) {
            return 0;
        }
        int left = minDepth(root.left);
        int right = minDepth(root.right);
        if (left == 0) {
            return right + 1;
        }
        if (right == 0) {
            return left + 1;
        }
        return Math.min(left, right) + 1;
    }

解题2：

层序遍历，这种效率是较高的

    public int minDepth(TreeNode root) {
        if (root == null) {
            return 0;
        }
        Queue<TreeNode> queue = new ArrayDeque<>();
        queue.offer(root);
        int level = 0;
        while (!queue.isEmpty()) {
            int size = queue.size();
            for (int i = 0; i < size; i++) {
                TreeNode poll = queue.poll();
                if (poll.left != null) {
                    queue.offer(poll.left);
                }
                if (poll.right != null) {
                    queue.offer(poll.right);
                }
                // 这个就是叶子节点，只要遇到第一个叶子节点，就会返回值
                if (poll.left == null && poll.right == null) {
                    return ++level;
                }
            }
            level++;
        }
        return level;
    }

226. 翻转二叉树

给你一棵二叉树的根节点 root ，翻转这棵二叉树，并返回其根节点。

解题思路：

很简单的一道递归调用，将节点的左右节点互相调换即可。

class Solution {
    public TreeNode invertTree(TreeNode root) {
        dsf(root);
        return root;
    }

    public void dsf(TreeNode node) {
        if (node == null) {
            return;
        }
        TreeNode tmp = node.left;
        node.left = node.right;
        node.right = tmp;
        dsf(node.right);
        dsf(node.left);
    }
}

根据后缀表达式，构建一颗树。

 

    // 根据后缀表达式生成树
    public TreeNode constructExpressionTree(String[] token) {
        Stack<TreeNode> stack = new Stack<>();

        for (String s : token) {
            switch (s) {
                case "+", "-", "*", "/" -> {
                    TreeNode right = stack.pop();
                    TreeNode left = stack.pop();
                    TreeNode parent = new TreeNode(s);
                    parent.right = right;
                    parent.left = left;
                    stack.push(parent);
                }
                default -> {
                    stack.push(new TreeNode(s));
                }
            }
        }
        return stack.peek();
    }

105 、从前序与中序遍历序列构造二叉树

给定两个整数数组 preorder 和 inorder ，其中 preorder 是二叉树的先序遍历， inorder 是同一棵树的中序遍历，请构造二叉树并返回其根节点。

解题思路

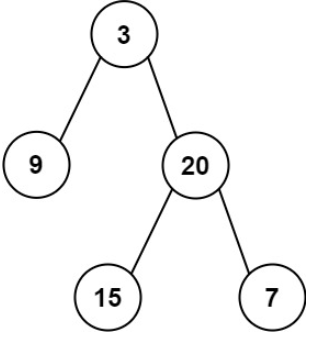
preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]

  1. 前序遍历，第一个节点肯定是头节点。确定头结点的值，可以在中序遍历中定位到头节点位置
  2. 中序数组中，头节点左侧是左子树，右侧是右子树
  3. 根据中序数组中判断出来的左右子树，可以在前序数组中分割出左右子树。
  4. 这样，就得到了根节点，左子树的前序和中序数组，右子树的前序和中序数组。就找到了递归的条件
  5. 递归结束条件，如果一个节点没有左右子树，说明前序数组和中序数组长度为0,。
public class Test105 {
    public TreeNode buildTree(int[] preorder, int[] inorder) {
        if (preorder.length == 0 || inorder.length == 0) {
            return null;
        }
        int rootValue = preorder[0];
        TreeNode root = new TreeNode(rootValue);

        for (int i = 0; i < inorder.length; i++) {
            // 找到中序数组中的根节点位置，左边是左子树，右边是右子树
            if (rootValue == inorder[i]) {
                // 中序数组，划分成左右两边
                int[] inLeft = Arrays.copyOfRange(inorder, 0, i);
                int[] inRight = Arrays.copyOfRange(inorder, i + 1, inorder.length);

                // 前序数组，也划分成左右两边
                int[] preLeft = Arrays.copyOfRange(preorder, 1, i + 1);
                int[] preRight = Arrays.copyOfRange(preorder, i + 1, inorder.length);

                //递归调用
                root.left = buildTree(preLeft, inLeft);
                root.right = buildTree(preRight, inRight);

                break;
            }
        }
        return root;
    }
}

106、从中序与后序遍历序列构造二叉树

给定两个整数数组 inorder 和 postorder ，其中 inorder 是二叉树的中序遍历， postorder 是同一棵树的后序遍历，请你构造并返回这颗 二叉树 。

解题思路，和105题一样

    public TreeNode buildTree1(int[] inorder, int[] postorder) {
        if (postorder.length == 0 || inorder.length == 0) {
            return null;
        }
        int length = postorder.length;
        int rootValue = postorder[length-1];
        TreeNode root = new TreeNode(rootValue);

        for (int i = 0; i < length; i++) {
            // 找到中序数组中的根节点位置，左边是左子树，右边是右子树
            if (rootValue == inorder[i]) {
                // 中序数组，划分成左右两边
                int[] inLeft = Arrays.copyOfRange(inorder, 0, i);
                int[] inRight = Arrays.copyOfRange(inorder, i + 1, inorder.length);

                // 后序数组，也划分成左右两边
                int[] postLeft = Arrays.copyOfRange(postorder, 0, i );
                int[] postRight = Arrays.copyOfRange(postorder, i , inorder.length-1);

                //递归调用
                root.left = buildTree(inLeft,postLeft);
                root.right = buildTree(inRight,postRight);

                break;
            }
        }
        return root;
    }

3、二叉搜索树

给树的节点定义一个key，是不可用重复的。

二叉搜索树满足：节点的key大于左子树的key，小于右子树的key。

二叉搜索树的实现：

 1、先定义二叉查找树的节点

二叉查找树节点
    static class BSTTreeNode {
        int key;
        Object value;
        BSTTreeNode left;
        BSTTreeNode right;
        public BSTTreeNode(int key) {
            this.key = key;
        }
    }

 2、定义二叉查找树的方法

二叉查找树方法
public class BSTTree {
    // 根节点
    BSTTreeNode root;

    // 根据key，获取value
    public Object get(int key) {
        return doGet(root, key);
    }

    // 获得树中最小key关联的值
    public Object min() {
        return null;
    }

    // 获得树中最大key关联的值
    public Object max() {
        return null;
    }

    // 找到一个key的前驱（就是比他key小的最大的值）
    public Object successor(int key) {
        return null;
    }

    // 找到一个key的后继（就是比他key大的最小的值）
    public Object predecessor(int key) {
        return null;
    }

    // 根据key删除节点
    public Object delete(int key) {
        return null;
    }

    public void put(int key, Object value) {
        
    }
}

3、get方法的实现

循环或者递归，比较key的值，key比当前节点的key大，就往右子树找，key比当前节点的key小，就往左子树找，找不到就返回null。

递归
    // 根据key，获取value
    public Object get(int key) {
        return doGet(root, key);
    }

    private Object doGet(BSTTreeNode node, int key) {
        if (node == null) {
            return null;
        }

        if (node.key < key) {
            return doGet(node.right, key);// 向右找
        } else if (node.key > key) {
            return doGet(node.left, key); // 向左找
        } else {
            return node.value; // 找到了
        }
    }

非递归
    public Object get1(int key) {
        BSTTreeNode node = root;
        while (node != null) {
            if (node.key > key) {
                node = node.left;
            } else if (node.key < key) {
                node = node.right;
            } else {
                return node;
            }
        }
        return null;
    }

4.min方法的实现：沿着根节点，一直往左找

    // 获得树中最小key关联的值
    public Object min() {
        return min(root);
    }

    public Object min(BSTTreeNode bstTreeNode) {
        BSTTreeNode node = bstTreeNode;
        while (true) {
            if (node == null) {
                return node;
            } else {
                node = node.left;
            }
        }
    }

5、max方法的实现：沿着根节点，一直往右找


    // 获得树中最大key关联的值
    public Object max() {
        return max(root);
    }

    public Object max(BSTTreeNode bstTreeNode) {
        BSTTreeNode node = bstTreeNode;
        while (true) {
            if (node == null) {
                return node;
            } else {
                node = node.right;
            }
        }
    }

6、增加节点方法实现

  1. 分为两种，key已经存在了，就更新value，key不存在，就新增节点到树里面。
  2. 判断key是否存在，也要用到查找逻辑，可以在get的基础上进行修改。
  3. 首先，如果树是空的，那么直接创建节点赋值给root
  4. 查找树中的key，比较大小，往左或者往右进行查找
  5. 如果查找到了，就直接修改value的值。
  6. 如果找不到，说明需要新增，新增在那个节点下面呢？因此要定义一个临时变量，记录4步骤中查到的最后一个不为null的节点。
  7. 得到6中的节点，判断key的值，选择插入这个节点的左边还是右边。
    // key存在，更新，key不存在，新增
    public void put(int key, Object value) {
        BSTTreeNode add = new BSTTreeNode(key, value);
        BSTTreeNode node = root;
        if (root == null) {
            root = add;
        }

        BSTTreeNode parent = null;
        while (node != null) {
            parent = node; // parent 记录循环中的最后一个节点
            if (node.key > key) {
                node = node.left;
            } else if (node.key < key) {
                node = node.right;
            } else {
                // 找到了，更新操作
                node.value = value;
                return;
            }
        }
        // 没有找到，新增
        if (parent.key > key) {
            parent.left = add;
        } else {
            parent.right = add;
        }
    }

7、删除一个节点

  1. 删除节点没有左孩子，将右孩子给parent
  2. 删除节点没有右孩子，将左孩子给parent
  3. 删除节点没有左右孩子，已经被1,2两个场景包括了
  4. 删除节点左右孩子都有：
    1. 首先找到被删除节点的后继节点（其实就是去右子树中一直往左找到的最后一个）
    2. 如果找到的后继节点与要删除的节点相邻，说明这个后继节点没有左节点，可以直接把这个后继节点顶上
    3. 如果不相邻，把这个后继节点的右孩子顶到后继节点的位置（后继节点不可能有左孩子），然后把后继节点取代被删除节点就可以。
    // 根据key删除节点
    public Object delete(int key) {
        BSTTreeNode node = root;
        BSTTreeNode parent = null;
        while (node != null) {
            if (key < node.key) {
                parent = node;
                node = node.left;
            } else if (key > node.key) {
                parent = node;
                node = node.right;
            } else {
                // node就是当前节点，就不需要给parent赋值了
                break;
            }
        }

        if (node == null) {
            // 没找到这个节点
            return null;
        }

        // 删除操作
        if (node.left == null) {
            // 没有左孩子，那么就把右孩子顶上去
            shift(parent, node, node.right);
        } else if (node.right == null) {
            // 没有右孩子，那么就把左孩子顶上去
            shift(parent, node, node.left);
        } else {
            // 左右孩子都有

            // 先找后继节点，后继节点肯定是去右子树中去寻找的
            BSTTreeNode preNode = node.right;
            BSTTreeNode preParent = node;
            // 后继节点肯定就是一直向左找的哪个节点。
            while (preNode.left != null) {
                preParent = preNode;
                preNode = preNode.left;
            }

            // 如果后继节点和待删除节点不相邻,说明preParent发生了变化
            if (preParent != node) {
                // 先处理后继节点的后事 
                // --- 其实就是把后继节点的右孩子，提升，因为后继节点不可能有左孩子
                shift(preParent, preNode, preNode.right);
                preNode.right = node.right;
            }

            // 后继节点取代被删除节点
            shift(parent, node, preNode);
            preNode.left = node.left;
        }
        return node.value;
    }

8、找到一个节点的先驱节点

  1. 如果一个节点有左子树，那么这个节点就是左子树中最大的哪个节点
  2. 如果一个节点没有左子树
    1. 这个节点就是他自左边来的最近的祖先节点 （3的是2,5的是4）
    2. 如果没有自左边来的最近的祖先节点，那么没有这个节点（1没有）

    // 找到一个key的前驱（就是比他key小的最大的值）
    public Object successor(int key) {
        BSTTreeNode node = root;
        BSTTreeNode ancestorFromLeft = null; // 记录从左而来的祖先节点
        while (node != null) {
            if (key < node.key) {
                node = node.left;
            } else if (key > node.key) {
                // 往右边查找，说明这个祖先节点是从左边来的
                ancestorFromLeft = node;
                node = node.right;
            } else {
                break;
            }
        }

        if (node == null) {
            return null; //没找到
        }

        if (node.left != null) {
            //存在左子树，那么就返回左子树中最大的一个值
            return max(node.left);
        }

        // 不存在左子树，那么就找左边来的祖先节点，距离自己最近的一个
        // 因为ancestorFromLeft每次都在更新，所以当前的ancestorFromLeft就是目标值。

        return ancestorFromLeft == null ? null : ancestorFromLeft.value;
    }

9、找到一个节点的后继节点 --- 与8是对称的

  1. 节点有右子树，那么节点就是右子树中的最小值
  2. 节点没有右子树：
    1. 这个节点就是他右边来的祖先的最近一个
    // 找到一个key的后继（就是比他key大的最小的值）
    public Object predecessor(int key) {
        BSTTreeNode node = root;
        BSTTreeNode ancestorFromRight = null;
        while (node != null) {
            if (key < node.key) {
                // 往左边查找，说明这个祖先节点是从右边来的
                ancestorFromRight = node;
                node = node.left;
            } else if (key > node.key) {
                node = node.right;
            } else {
                break;
            }
        }

        if (node == null) {
            return null; //没找到
        }
        if (node.right != null) {
            return min(node.right);
        }
        return ancestorFromRight == null ? null : ancestorFromRight.value;
    }

练习题：

LeetCode 450,700,701三题就对应了二叉查找树的增删查。对于删除操作，比较复杂要多加练习。

98. 验证二叉搜索树

给你一个二叉树的根节点 root ，判断其是否是一个有效的二叉搜索树。

解题思路：

  1. 节点比左孩子大，比右孩子小（不包含等于的情况）
  2. 节点比左子树中最大的值大，比右子树中最小的值小 --- （1就可以合并到2中）
  3. 根据2的条件，递归
public class Test98 {
    public boolean isValidBST(TreeNode root) {
        return dsf(root);
    }

    // 递归方法
    public boolean dsf(TreeNode node) {
        // 节点是空，或者节点是叶子节点，符合二叉搜索树，可以返回true
        if (node == null || (node.left == null && node.right == null)) {
            return true;
        }
        int val = node.val;
        // 定义一个临时变量
        TreeNode tmp = node;
        
        // 到左子树中找最大的值，要求比当前节点值小，否则返回false
        if (tmp.left != null) {
            tmp = tmp.left;
            while (tmp.right != null) {
                tmp = tmp.right;
            }
            if (tmp.val >= val) {
                return false;
            }
        }

        // 到右子树中找最小的值，要求比当前节点值大，否则返回false
        tmp = node;
        if (node.right != null) {
            tmp = tmp.right;
            while (tmp.left != null) {
                tmp = tmp.left;
            }
            if (tmp.val <= val) {
                return false;
            }
        }

        // 递归调用
        return dsf(node.left) && dsf(node.right);
    }
}

938. 二叉搜索树的范围和

给定二叉搜索树的根结点 root，返回值位于范围 [low, high] 之间的所有结点的值的和。

----- 这一题，总的来说还是DSF更好理解，效率更好

解题思路：

  1. 深度优先遍历，因为是二叉查找树，因此树的节点是有顺序的。
  2. 如果当前节点比high大，那么只要在左子树中遍历就可以了
  3. 如果当前节点比low小，那么只要在右子树找那个遍历就可以了
  4. 否则，值就是当前节点的值 加上左子树、右子树中符合要求的节点的和。
class Solution {
    public int rangeSumBST(TreeNode root, int low, int high) {
        if (root == null) {
            return 0;
        }

        if (root.val > high) {
            return rangeSumBST(root.left, low, high);
        }

        if (root.val < low) {
            return rangeSumBST(root.right, low, high);
        }

        return root.val + rangeSumBST(root.left, low, high) + rangeSumBST(root.right, low, high);
    }
}

解题思路2：

  1. 广度优先遍历，同样利用二叉查找树的特性可以进行剪枝
  2. 实现思路和DSF一样，只不过是变成了BSF
  3. 注意一点：
    1. ArrayDeque是能插入null作为节点的
    2. LinkedList可以插入null作为节点
class Solution {
    public int rangeSumBST(TreeNode root, int low, int high) {
        if (root == null) {
            return 0;
        }

        int res = 0;
        Queue<TreeNode> queue = new LinkedList<>();
        queue.offer(root);
        while (!queue.isEmpty()) {
            int size = queue.size();
            for (int i = 0; i < size; i++) {
                TreeNode poll = queue.poll();
                if (poll == null) {
                    continue;
                }
                if (poll.val > high) {
                    queue.offer(poll.left);
                } else if (poll.val < low) {
                    queue.offer(poll.right);
                } else {
                    res += poll.val;
                    queue.offer(poll.left);
                    queue.offer(poll.right);
                }
            }
        }
        return res;
    }
}

1008. 前序遍历构造二叉搜索树

解题思路：

  1. 前序遍历，第一个值就是根节点，知道了根节点，遍历数组，一个个去插入节点即可。
class Solution {
    public TreeNode bstFromPreorder(int[] preorder) {
        if (preorder.length == 0) {
            return null;
        }
        TreeNode root = new TreeNode(preorder[0]);
        for (int i = 1; i < preorder.length; i++) {
            put(new TreeNode(preorder[i]), root);
        }
        return root;
    }

    public void put(TreeNode add, TreeNode node) {
        if (add == null) {
            return;
        }
        TreeNode preNode = null;
        while (node != null) {
            preNode = node;
            if (node.val > add.val) {
                node = node.left;
            } else if (node.val < add.val) {
                node = node.right;
            } else {
                break;
            }
        }

        if (preNode.val > add.val) {
            preNode.left = add;
            return;
        }

        if (preNode.val < add.val) {
            preNode.right = add;
            return;
        }
    }
}

235. 二叉搜索树的最近公共祖先

解题思路：

  1. 因为是二叉搜索树，因此最近的公共祖先-----转化为，找到最近的一个节点，p 和 q在这个节点的左右两边
  2. 注意，p或者q也可以是公共祖先

递归写法

class Solution {
    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
        if (root == null) {
            return null;
        }
        TreeNode node = root;

        TreeNode min = p.val > q.val ? q : p;
        TreeNode max = p.val > q.val ? p : q;

        if (node.val >= min.val && node.val <= max.val) {
            return node;
        }

        if (node.val > max.val) {
            return lowestCommonAncestor(node.left, p, q);
        } else {
            return lowestCommonAncestor(node.right, p, q);
        }
    }
}

非递归写法

class Solution {
    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
        TreeNode node = root;

        TreeNode min = p.val > q.val ? q : p;
        TreeNode max = p.val > q.val ? p : q;

        while (true) {
            if (node.val >= min.val && node.val <= max.val) {
                return node;
            } else if (node.val > max.val) {
                node = node.left;
            } else {
                node = node.right;
            }
        }
    }
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/577217.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

CAPL(vTESTStudio) - CAPL控制RS232继电器

CAPL(vTESTStudio) - CAPL控制RS232继电器

目录 为什么要使用CAPL控制继电器？ 一、RS232继电器选择 二、继电器通信协议
阅读更多...
AList 一个支持多种存储的文件列表程序，使用 Gin 和 Solidjs。

AList 一个支持多种存储的文件列表程序，使用 Gin 和 Solidjs。

一个支持多种存储&#xff0c;支持网页浏览和 WebDAV 的文件列表程序&#xff0c;由 gin 和 Solidjs 驱动。 特点 使用简单 AList 从一开始就设计为易于安装&#xff0c;并且可以在所有平台上使用。 多种存储 AList 支持多个存储提供商&#xff0c;包括本地存储、阿里云盘、O…
阅读更多...
大数据治理入门系列：数据治理

大数据治理入门系列：数据治理

在信息经济时代&#xff0c;数据是企业的一大关键资产。为了制定科学、有效、合理的决策&#xff0c;企业需要收集大量的数据并进行各种数据分析&#xff0c;为决策提供依据。在此过程中&#xff0c;收集数据的速度、数据的质量和可靠性、对数据的分析过程、合适的分析工具等&a…
阅读更多...
三十四、数学知识——约数（试除法 + 约数个数 + 约数之和 + 欧几里得算法）

三十四、数学知识——约数（试除法 + 约数个数 + 约数之和 + 欧几里得算法）

约数相关算法主要内容 一、基本思路1、定义2、试除法——求一个数的所有约数3、约数个数4、约数之和5、欧几里得算法——辗转相除法&#xff08;求解最大公约数&#xff09; 二、Java、C语言模板实现三、例题题解 一、基本思路 1、定义 约数&#xff1a; 约数是指一个数&…
阅读更多...
利用百度API进行植物识别

利用百度API进行植物识别

植物识别_拍照识别植物-百度AI开放平台百度AI植物识别,支持识别超过2万种通用植物和近8千种花卉&#xff0c;接口返回植物的名称&#xff0c;并获取百科信息&#xff0c;适用于拍照识图类APP中https://ai.baidu.com/tech/imagerecognition/plant 偶然看到的&#xff0c;不过真…
阅读更多...
STM32F103C8T6+2.4寸SPI TFT触摸屏代码+标准库 项目开发

STM32F103C8T6+2.4寸SPI TFT触摸屏代码+标准库 项目开发

目录 模块清单&#xff1a; 模块介绍&#xff1a; 1&#xff1a;STM32F103C8T6 2&#xff1a;2.4寸SPI TFT触摸屏 项目结果展示 2.4寸 TFT SPI显示触摸屏 2.4寸 SPI TFT 显示触摸屏代码下载链接&#xff1a; (1条消息) 2.4寸SPITFT显示触摸屏资源-CSDN文库 模块清单&#x…
阅读更多...
Vue后台管理系统【附源码】

Vue后台管理系统【附源码】

登录 – 完成 路由拦截 – 完成 商品管理&#xff08;增加、编辑、搜索、删除&#xff09; – 完成 角色管理&#xff08;增加、编辑、搜索、删除、权限管理&#xff09; – 完成 交易订单&#xff08;增加、编辑、搜索、删除&#xff09; – 完成 用户管理&#xff08;增加、编…
阅读更多...
在Centos Stream 9上Docker的实操教程 - 实操准备篇

在Centos Stream 9上Docker的实操教程 - 实操准备篇

在Centos Stream 9上Docker的实操教程 - 实操准备篇 认识Docker准备Centos Stream 9安装Docker更新仓库绕不开的HelloWorld结语 认识Docker 什么都要实操了&#xff0c;你还不知道Docker是什么&#xff1f;网上关于Docker的介绍一搜一大把&#xff0c;博主就不必浪费时间去侃侃…
阅读更多...
ESP32-OTA

ESP32-OTA

文章目录 1. 什么是OTA&#xff1f;2. OTA的基本原理3. ESP32远程OTA步骤&#xff1a;3.1 将需要升级的程序放在该目录下3.2 启动HTTP服务器3.3 配置3.4 烧录程序3.5 上电测试ESP32端 4. 问题&#xff1a;5. 通过命令控制OTA6. 参考&#xff1a; 1. 什么是OTA&#xff1f; OTA…
阅读更多...
如何用 GPT-4 帮你写游戏（以24点游戏举例）

如何用 GPT-4 帮你写游戏（以24点游戏举例）

目录 给我一个24点游戏 游戏规则 GPT给的代码 ​改进 再改进 最近呢掀起了一阵GPT-4的热潮&#xff0c;很多人都想用GPT-4&#xff0c;这里呢我就打一个广告&#xff08;嘿嘿&#xff09;&#xff0c;如果不知道国内如何使用GPT的&#xff0c;可以看看这个博客&#xff1a;G…
阅读更多...
STC89C52+DHT20设计的环境温湿度检测仪

STC89C52+DHT20设计的环境温湿度检测仪

一、项目背景 本项目基于STC89C52单片机和DHT20温湿度传感器，实现了一款环境温湿度检测仪。通过传感器采集环境的温度和湿度数据，利用IIC接口的OLED显示屏显示出来，便于用户实时监测环境温湿度状态。 在现代社会，人们对环境温湿度的要求越来越高。无论是工作场所还是居住…
阅读更多...
局部特征匹配(LoFTR) 基于全局匹配的光流学习(GMFlow)

局部特征匹配(LoFTR) 基于全局匹配的光流学习(GMFlow)

文章目录 特征匹配&#xff08;稀疏匹配与稠密匹配&#xff09;《LoFTR: Detector-Free Local Feature Matching with Transformers》【CVPR21】《GMFlow: Learning Optical Flow via Global Matching》【CVPR22】光流的定义第一个问题第二个问题方法该框架下存在的一个问题 Pr…
阅读更多...
智慧园区管理平台优势详解

智慧园区管理平台优势详解

随着数字化和智能化的时代到来&#xff0c;越来越多的园区开始使用智慧园区管理平台来提高管理效率&#xff0c;降低管理成本和提升服务质量。智慧园区管理平台是一种通过智能化技术与物联网技术进行连接&#xff0c;对园区进行综合管理、智能化监控的信息化平台。下面将详细介…
阅读更多...
大数据：云平台，阿里云VPC创建，创建安全组，云服务器ECS，

大数据：云平台，阿里云VPC创建，创建安全组，云服务器ECS，

大数据&#xff1a;云平台 2022找工作是学历、能力和运气的超强结合体&#xff0c;遇到寒冬&#xff0c;大厂不招人&#xff0c;可能很多算法学生都得去找开发&#xff0c;测开 测开的话&#xff0c;你就得学数据库&#xff0c;sql&#xff0c;oracle&#xff0c;尤其sql要学&…
阅读更多...
Seata之@GlobalTransactional验证

Seata之@GlobalTransactional验证

下订单 -> 减库存 -> 扣余额 -> 改&#xff08;订单&#xff09;状态 1.数据库初始情况&#xff1a; 2.正常下单 http://localhost:2001/order/create?userId1&productId1&count10&money100 3.超时异常&#xff0c;没加GlobalTransactional 模拟Accou…
阅读更多...
RabbitMQ系列（24）--RabbitMQ集群搭建

RabbitMQ系列（24）--RabbitMQ集群搭建

前言&#xff1a;当RabbitMQ服务器遇到内存崩溃、机器掉电或者主板故障等情况&#xff0c;该怎么办?单台RabbitMQ服务器可以满足每秒1000条消息的吞吐量&#xff0c;那如果应用需要RabbitMQ服务满足每秒10万条消息的吞吐量呢?购买昂贵的服务器来增强单机RabbitMQ服务的性能不…
阅读更多...
阿里云ECS部署chat-web代理访问

阿里云ECS部署chat-web代理访问

1、ECS服务器申请 使用阿里云账号购买了一个美国&#xff08;弗吉尼亚&#xff09;的2C/2G的CentOS7.9 x64服务器。 2、系统版本升级 CentOS7.9默认的python和pip版本都是3.6的&#xff0c;需要升级到3.9以上&#xff0c;升级步骤百度&#xff0c;大致如下&#xff1a; wget…
阅读更多...
vue diff算法与虚拟dom知识整理(12) patch精细化比较新增子节点

vue diff算法与虚拟dom知识整理(12) patch精细化比较新增子节点

上文中我们编写了patch函数中对相同节点的几种处理 将简单的都写完了 但还留下了最麻烦的子节点比较 既新旧节点都有子节点 需要 精细化比较 我们先将src下的入口文件index.js 代码改成这样 import h from "./snabbdom/h"; import patch from "./snabbdom/pat…
阅读更多...
C++实现Canny边缘检测（原理+底层代码）

C++实现Canny边缘检测（原理+底层代码）

文章目录 一、算法原理二、环境配置三、算法详解3.1、数据结构 Mat3.2、高斯滤波器的C实现3.3、用一阶偏导有限差分计算梯度幅值和方向 三、项目实战&#xff1a;C实现Canny边缘检测 一、算法原理 canny边缘检测算法步骤&#xff1a; 1、使用高斯滤波器对图像进行平滑处理。 2、…
阅读更多...
recurdyn履带问题

recurdyn履带问题

1.问题&#xff1a;整车履带仿真出错&#xff0c;车辆越障时遇到障碍物直接弹开 思路&#xff1a; 关于这类模型需要调节履带和地面之间的接触参数、Bushing force&#xff0c;还有驱动函数。 弹飞了是因为接触刚度太大了&#xff0c;调小一些&#xff0c;在100以内继续调节…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023