题单介绍：

精选 100 道力扣（LeetCode）上最热门的题目，适合初识算法与数据结构的新手和想要在短时间内高效提升的人，熟练掌握这 100 道题，你就已经具备了在代码世界通行的基本能力。

题单介绍：

题目：2. 两数相加 - 力扣（Leetcode）

题目的接口：

解题思路：

代码：

过过过过啦！！！！

题目：4. 寻找两个正序数组的中位数 - 力扣（Leetcode）

题目的接口：

解题思路：

代码：

过过过过啦！！！！

写在最后：

题目：2. 两数相加 - 力扣（Leetcode）

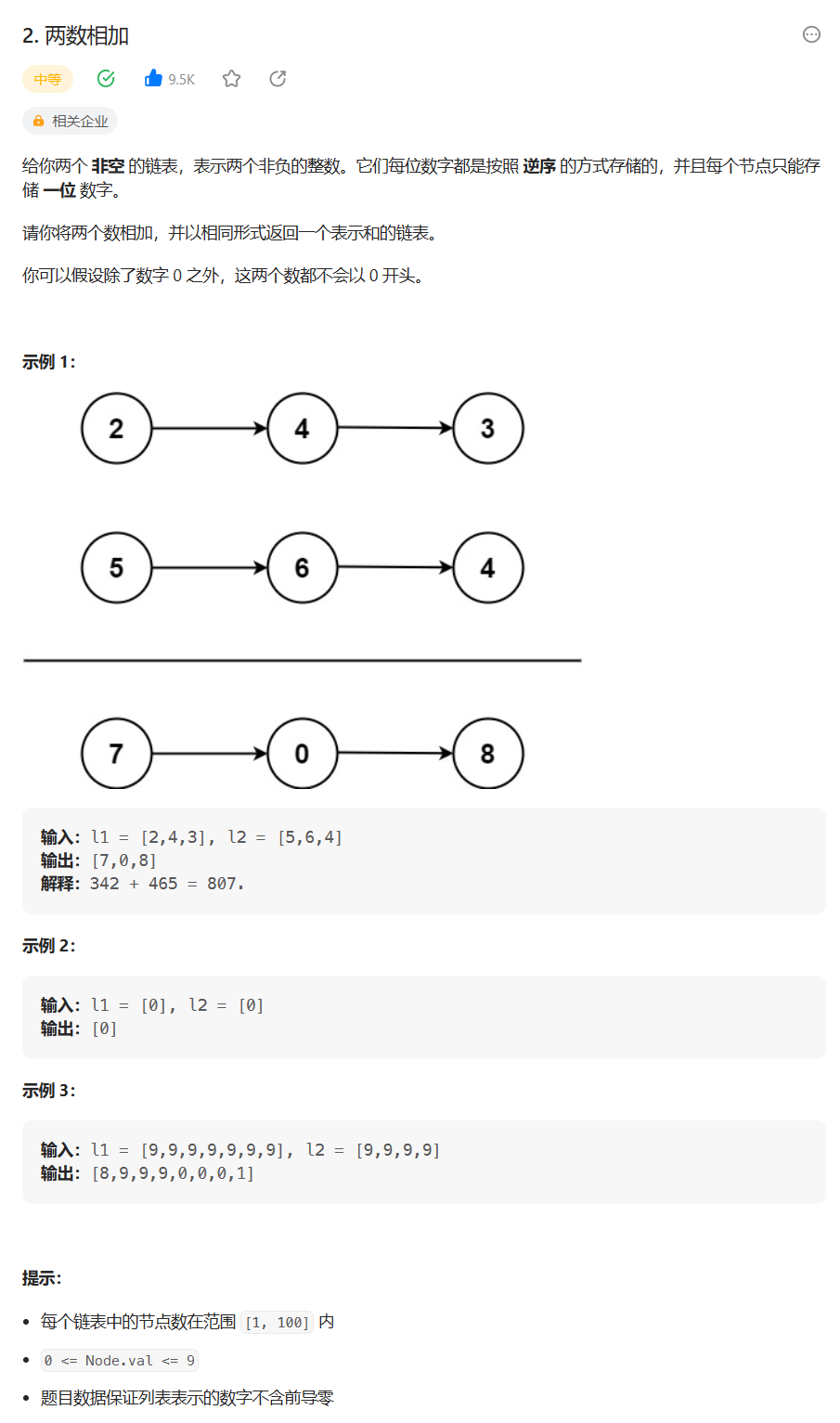
题目的接口：

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    ListNode* addTwoNumbers(ListNode* l1, ListNode* l2) {

    }
};

解题思路：

这道题目其实不难啊，

所以我就直接上手做了，

导致代码其实写的不是很好啊，可以优化的地方不少，

不过整体思路是没有问题的，

这道题就是简单模拟加法进位，不过因为是在链表上实现，

所以对链表知识掌握有一定的要求，具体思路如下：

1. 建一个新链表

2. 计算进位并插入

3. 返回新链表的头结点

代码如下：

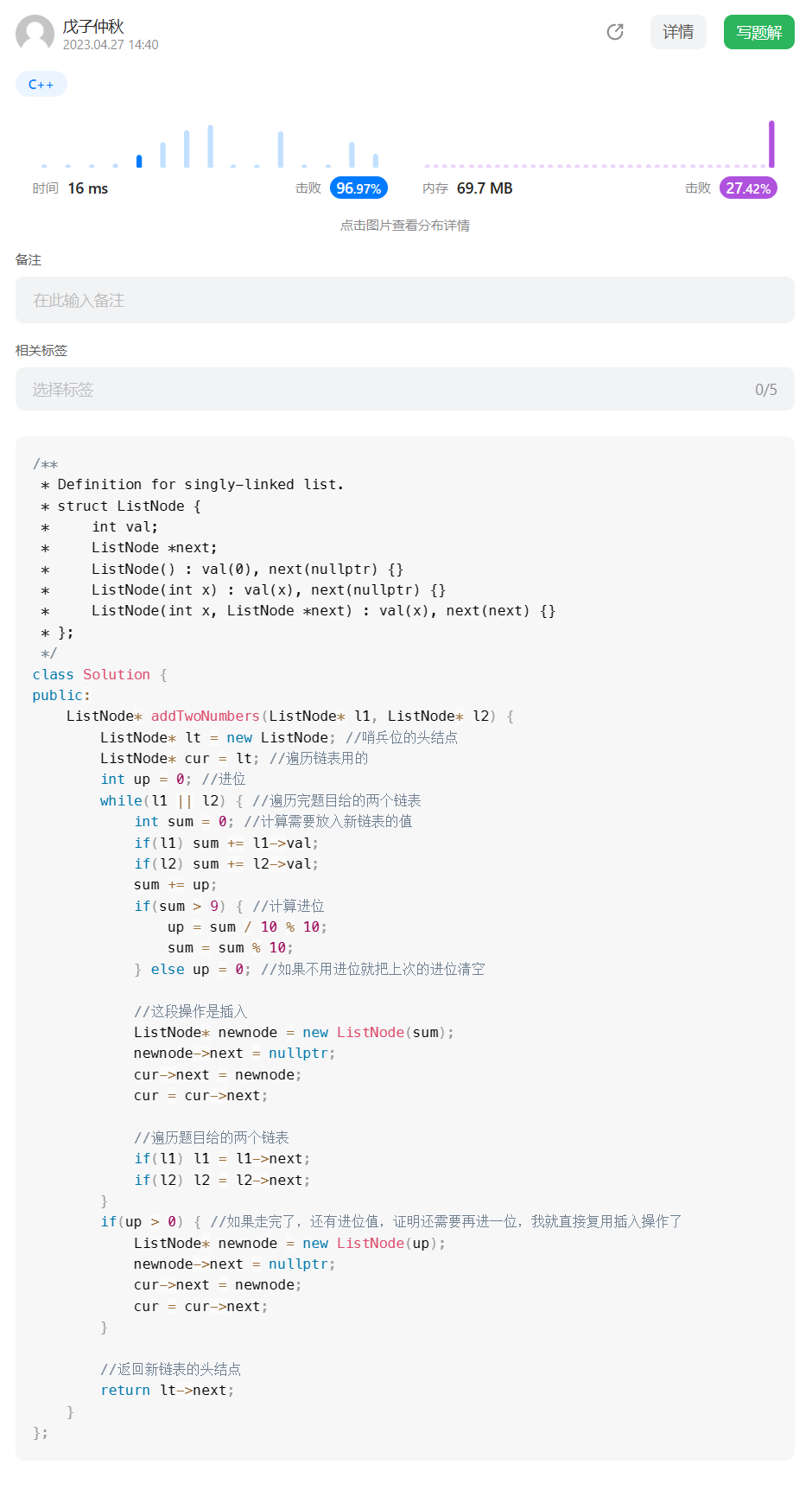
代码：

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    ListNode* addTwoNumbers(ListNode* l1, ListNode* l2) {
        ListNode* lt = new ListNode; //哨兵位的头结点
        ListNode* cur = lt; //遍历链表用的
        int up = 0; //进位
        while(l1 || l2) { //遍历完题目给的两个链表
            int sum = 0; //计算需要放入新链表的值
            if(l1) sum += l1->val;
            if(l2) sum += l2->val;
            sum += up;
            if(sum > 9) { //计算进位
                up = sum / 10 % 10;
                sum = sum % 10;
            } else up = 0; //如果不用进位就把上次的进位清空

            //这段操作是插入
            ListNode* newnode = new ListNode(sum);
            newnode->next = nullptr;
            cur->next = newnode;
            cur = cur->next;

            //遍历题目给的两个链表
            if(l1) l1 = l1->next;
            if(l2) l2 = l2->next;
        }
        if(up > 0) { //如果走完了，还有进位值，证明还需要再进一位，我就直接复用插入操作了
            ListNode* newnode = new ListNode(up);
            newnode->next = nullptr;
            cur->next = newnode;
            cur = cur->next;
        }

        //返回新链表的头结点
        return lt->next;
    }
};

过过过过啦！！！！

题目：4. 寻找两个正序数组的中位数 - 力扣（Leetcode）

题目的接口：

class Solution {
public:
    double findMedianSortedArrays(vector<int>& nums1, vector<int>& nums2) {

    }
};

解题思路：

这道题不简单啊，但是如果不考虑复杂度其实挺简单的，

我先把不考虑时间复杂的方法贴出来：

class Solution {
public:
    double findMedianSortedArrays(vector<int>& nums1, vector<int>& nums2) {
        vector<int> sum(nums1);
        for(auto e : nums2) sum.push_back(e); //合并数组
        sort(sum.begin(), sum.end()); //排序
        if(sum.size() % 2 != 0) { //分情况取中位数即可
            return sum[sum.size() / 2];
        }
        else {
            return ((double)sum[sum.size() / 2] + (double)sum[sum.size() / 2 - 1]) / 2; 
        }
        return 1;
    }
};

简单来讲就是合并数组，sort，然后取中位数即可。（实际上是能过的）

如果需要严格按照题目的时间复杂的求解的话，

那就只能使用二分法了。

我们可以将这题转换成用二分查找两个有序数组中第k个最小的数，

我们需要分多种情况考虑，代码如下：

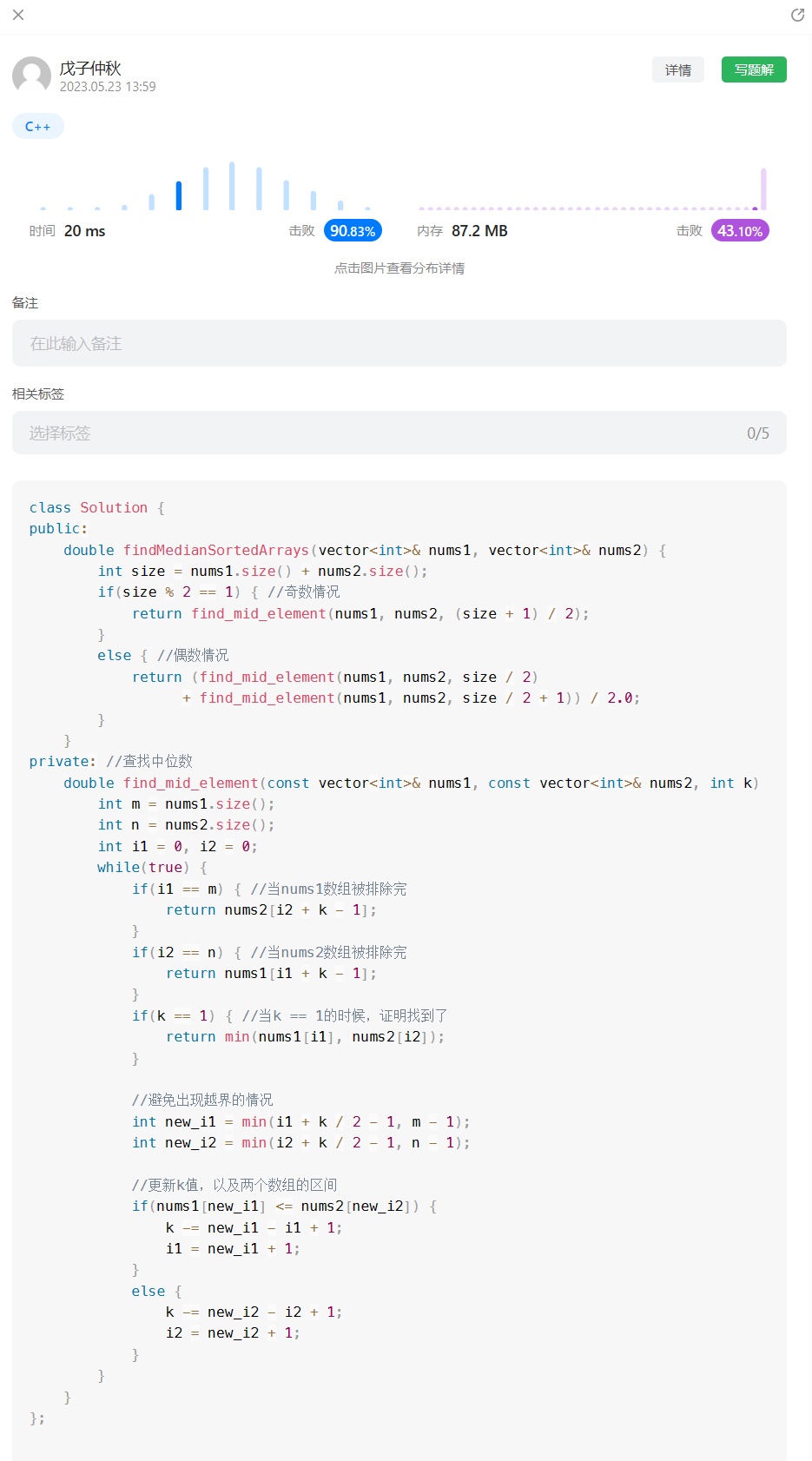
代码：

class Solution {
public:
    double findMedianSortedArrays(vector<int>& nums1, vector<int>& nums2) {
        int size = nums1.size() + nums2.size();
        if(size % 2 == 1) { //奇数情况
            return find_mid_element(nums1, nums2, (size + 1) / 2);
        }
        else { //偶数情况
            return (find_mid_element(nums1, nums2, size / 2) 
                  + find_mid_element(nums1, nums2, size / 2 + 1)) / 2.0;
        }
    }
private: //查找中位数
    double find_mid_element(const vector<int>& nums1, const vector<int>& nums2, int k) {
        int m = nums1.size();
        int n = nums2.size();
        int i1 = 0, i2 = 0;
        while(true) { 
            if(i1 == m) { //当nums1数组被排除完
                return nums2[i2 + k - 1];
            }
            if(i2 == n) { //当nums2数组被排除完
                return nums1[i1 + k - 1];
            }
            if(k == 1) { //当k == 1的时候，证明找到了   
                return min(nums1[i1], nums2[i2]);
            }

            //避免出现越界的情况
            int new_i1 = min(i1 + k / 2 - 1, m - 1);
            int new_i2 = min(i2 + k / 2 - 1, n - 1);

            //更新k值，以及两个数组的区间
            if(nums1[new_i1] <= nums2[new_i2]) {
                k -= new_i1 - i1 + 1;
                i1 = new_i1 + 1;
            }
            else {
                k -= new_i2 - i2 + 1;
                i2 = new_i2 + 1;
            }
        }
    }
};