[数据结构] AVL树的插入旋转 和 概念理解

news2024/10/7 2:32:30

文章目录

  • 定义 && 性质
    • 定义
    • 性质
  • 实现
    • 思路
    • 架构
    • 节点
    • AVL树
      • 框架
      • Insert（插入）
      • 左单旋
      • 右单旋
      • 左右双旋
      • 右左双旋

定义 && 性质

定义

二叉搜索树虽可以缩短查找的效率，但 如果数据有序或接近有序二叉搜索树将退化为单支树，查找元素相当于在顺序表中搜索元素，效率低下。

而AVL树可以较好的解决上述问题：当向二叉搜索树中插入新结点后，如果能保证每个结点的左右子树高度之差的绝对值不超过1(需要对树中的结点进行调整)，即可降低树的高度，从而减少平均搜索长度。

性质

AVL树是一种 自平衡二叉搜索树，严格满足以下性质：

  1. 对于任何一个节点，其左子树和右子树的高度差（即平衡因子）不超过1。
  2. AVL树的每个节点存储的键值大于其左子树中所有节点的键值，小于其右子树中的所有节点的键值。这也是二叉搜索树的基本性质。
  3. 它的左右子树都是AVL树

实现

思路

  • 核心思想是通过旋转操作保持树的平衡性
  • 在 AVL 树中，每个节点都有一个平衡因子，并且平衡因子的值只能是 0，1 或 -1
  • 当插入或删除节点导致某个节点的平衡因子绝对值大于 1 时，就需要通过旋转操作来调整整棵树的平衡性。

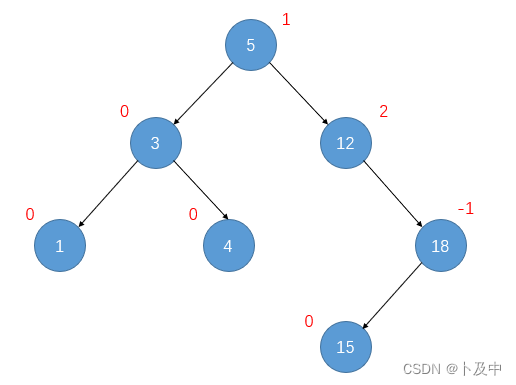
在这里插入图片描述

当右子树高的时候，平衡因子+1，当左子树高时，平衡因子-1
对上述的树，就需要通过旋转让其平衡

架构

  • 包含两个结构体，一个用来进行节点的实现，一个用于实现 AVLTree 的各项功能
#pragma once

template<class K, class V>
struct AVLTreeNode //节点
{
	// 成员变量 和 成员函数
};

template<class K, class V>
struct AVLTree
{
	typedef AVLTreeNode<K, V> Node; //重命名
public:
	// 公有成员函数
private:
	// 私有成员函数
private:
	// 成员变量
	Node* _root = nullptr;
};

节点

  1. 将节点的实现在结构体中，节点包含 左右子树指针、父节点指针、键值对和平衡因子。
  2. AVL 树的节点需要记录其左右子树指针和父节点指针，以支持 AVL 树的旋转操作。同时还需要记录键值对，以实现对键值对信息的存储。最后，需要记录平衡因子用于判断是否需要进行旋转的操作。
  3. 用一个构造函数初始化成员变量
template<class K, class V>
struct AVLTreeNode //节点
{
	AVLTreeNode<K, V>* _left; //指向左子树
	AVLTreeNode<K, V>* _right; //指向右子树
	AVLTreeNode<K, V>* _parent; //指向父节点

	pair<K, V> _kv; //键值对
	int _bf; //平衡因子

	AVLTreeNode(const pair<K, V> & kv)
		:_left(nullptr)
		,_right(nullptr)
		,_parent(nullptr)
		,_kv(kv)
		,_bf(0)
	{}
};

AVL树

框架

  • 将待实现的功能放到这里
  • 成员变量为_root根节点
template<class K, class V>
struct AVLTree
{
	typedef AVLTreeNode<K, V> Node; //重命名
public:
	// 插入
	bool Insert(const pair<K, V>& kv)
	{}
	
	// 中序遍历/打印
	void InOrder()
	{}
	
	//判断是否平衡
	bool IsBalance()
	{}

private:
	// 判断是否平衡
	bool _IsBalance(Node* root)
	{}

	// 求AVL树最大高度
	int Height(Node* root)
	{}

	// 左单旋
	void RotateL(Node* parent)
	{}

	// 右单旋
	void RotateR(Node* parent)
	{}

	// 左右双旋
	void RotateLR(Node* parent)
	{}

	// 右左双旋
	void RotateRL(Node* parent)
	{}

	void _InOrder(Node* root)
	{}

private:
	// 根节点
	Node* _root = nullptr;
};

Insert（插入）

插入过程主要分为两个步骤：

  1. 搜索树的插入过程。从根节点开始，与新插入的节点的键值比较大小，向左（小于当前节点的键值）或向右（大于当前节点的键值）递归地查找插入位置；如果要插入的节点的键值已经存在，则返回 false。
  2. 插入新的节点。将新节点插入到搜索树的合适位置，并更新其父节点指针。同时，从新节点开始向上检查，计算所经过节点的平衡因子并进行适当的旋转操作以调整树的平衡。
bool Insert(const pair<K, V>& kv)
	{
		// 根为空时第一次插入直接创建新节点
		if (_root == nullptr)
		{
			_root = new Node(kv);
			return true;
		}

		Node* parent = nullptr;
		Node* cur = _root;

		// 搜索树的插入逻辑
		while (cur) {
			// 如果插入的节点值大，则插入右边
			if (kv.first > cur->_kv.first)
			{
				parent = cur;
				cur = cur->_right;
			}
			else if (kv.first < cur->_kv.first)
			{
				parent = cur;
				cur = cur->_left;
			}
			else
			{
				return false;
			}
		}

		// 如果要插入的节点的键值大于其父节点的键值，则将其作为右子节点；
		// 否则将其作为左子节点。
		cur = new Node(kv);
		if (parent->_kv.first < kv.first)
		{
			parent->_right = cur;
		}
		else
		{
			parent->_left = cur;
		}
		
		cur->_parent = parent; // 记录插入节点的父节点

		// 控制平衡
		// 1、更新平衡因子
		while (parent)
		{
			// cur在右边，则平衡因子++
			if (cur == parent->_right)
				++parent->_bf;
			// cur在左边，则平衡因子--
			else
				--parent->_bf;

			// 平衡因子 == 0，已经平衡
			if (parent->_bf == 0) {
				break;
			}
			// == 1，向上找
			else if (abs(parent->_bf) == 1) {
				parent = parent->_parent;
				cur = cur->_parent;
			}
			// == 2，此时parent所在子树已经不平衡了，需要旋转处理
			else if (abs(parent->_bf) == 2) {
				if (parent->_bf == 2 && cur->_bf == 1)
				{
					// 此时进行左单旋
					RotateL(parent);
				}
				else if (parent->_bf == -2 && cur->_bf == -1)
				{
					// 此时进行右单旋
					RotateR(parent);
				}
				else if (parent->_bf == -2 && cur->_bf == 1)
				{
					// 左右双旋
					RotateLR(parent);
				}
				else if (parent->_bf == 2 && cur->_bf == -1)
				{
					//右左双旋
					RotateRL(parent);
				}
				else
				{
					// 正常情况下不会出现该种情况，如果出现直接报错
					assert(false);
				}
			}
			else {
				// 正常情况下不会出现该种情况，如果出现直接报错
				assert(false);
			}
		}
		return true;
	}

左单旋

抽象图（思路）：

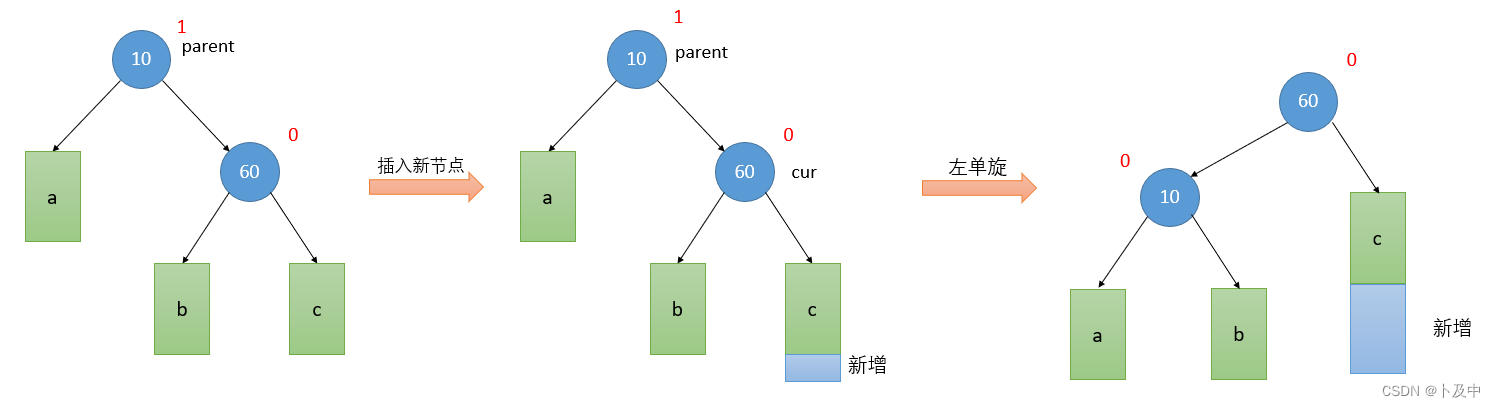
在这里插入图片描述

  1. 根据图中思路写代码：记录右侧节点和右侧节点的左子树节点。
  2. 将 subR 的左子树更改为 parent，同时将 parent 的父节点指向 subR。
  3. 将 parent 的右子树更改为 subRL，并更新 subRL 的父节点为 parent。
  4. 如果 parent 是根节点，则将 subR 设为新的根节点，并将 subR 的父节点设为 nullptr；否则将 subR 的父节点指向 parent 的父节点，并更新 parent 的父节点的左子树或右子树为 subR。
  5. 最后，将 subR 和 parent 的平衡因子都设置为 0。
void RotateL(Node* parent)
	{
		// 此时右子树的高度比左子树高2，记录右侧节点
		Node* subR = parent->_right;
		Node* subRL = subR->_left;


		// 目的需要将subR变为新的父节点（根节点）
 		// 将SubRL变为parent的子节点
		parent->_right = subRL;
		if (subRL)
			subRL->_parent = parent;

		// 创建此时父节点的头节点
		Node* ppNode = parent->_parent;
		subR->_left = parent;
		parent->_parent = subR; //此时subR到父节点的位置

		// 如果本来父节点为根
		if (_root == parent)
		{
			//将subR变为根
			_root = subR;
			subR->_parent = nullptr;
		}
		// 本来parent不为根节点
		else
		{
			// 将subR的_parent指向ppNode
			if (ppNode->_left == parent)
				ppNode->_left = subR;
			else
				ppNode->_right = subR;

			subR->_parent = ppNode;
		}
		// 此时平衡，更新平衡因子
		subR->_bf = parent->_bf = 0;
	}

右单旋

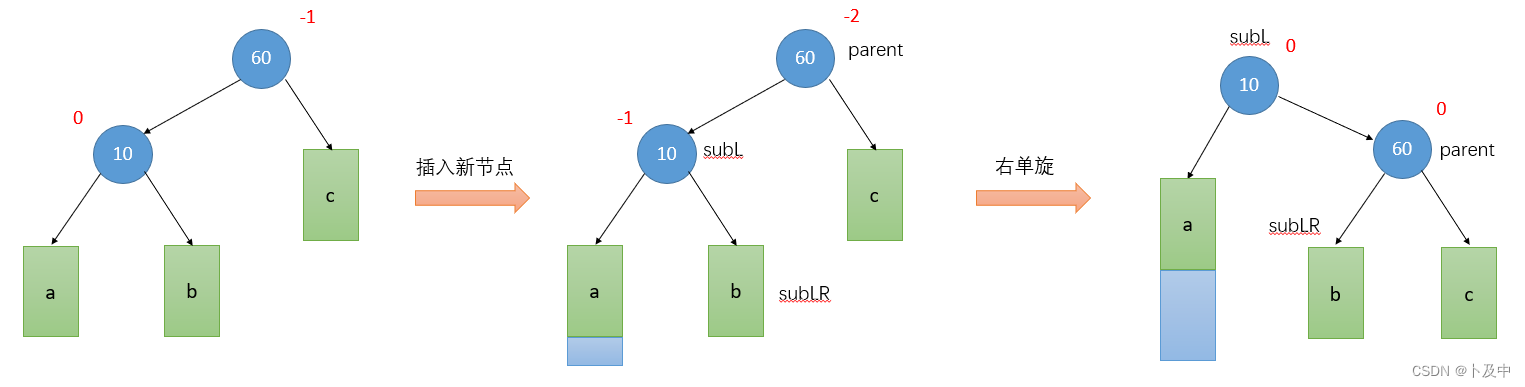
在这里插入图片描述

  1. 根据图片思路写代码：定义 subL 和 subLR 分别为 parent 节点的左孩子和 subL 节点的右孩子。
  2. 将 subLR 节点移动到 parent 节点的位置上，即 parent 的左孩子变成 subLR，subLR 的父节点变成 parent。
  3. 将 subL 节点移动到 subLR 节点的右边，subL 的右孩子变成 parent，parent 的父节点变成 subL。
  4. 如果原先 parent 节点是根节点，将 subL 节点设为新的根节点并将其父节点设置为空；如果不是根节点，则将 subL 节点移动到 parent 节点原来的父节点的位置上，并更新子节点的父节点。
  5. 更新 subL 和 parent 节点的平衡因子，均设为 0。
void RotateR(Node* parent)
	{
		// 获取左子树和左子树的右子树
		Node* subL = parent->_left;
		Node* subLR = subL->_right;

		// 旋转操作：将左子树的右子树变为 parent 的左子树
		parent->_left = subLR;
		if (subLR)
			subLR->_parent = parent;

		// 将 parent 变为左子树的右子树
		subL->_right = parent;
		parent->_parent = subL;

		// 如果 parent 原本是根节点，则设置新的根节点为 subL，否则需要调整 parent 的父节点
		Node* ppNode = parent->_parent;
		if (_root == parent)
		{
			_root = subL;
			subL->_parent = nullptr;
		}
		else
		{
			if (ppNode->_left == parent)
				ppNode->_left = subL;
			else
				ppNode->_right = subL;

			subL->_parent = ppNode;
		}

		// 更新平衡因子：旋转后，parent 和 subL 的平衡因子都变为 0
		subL->_bf = parent->_bf = 0;
	}

左右双旋

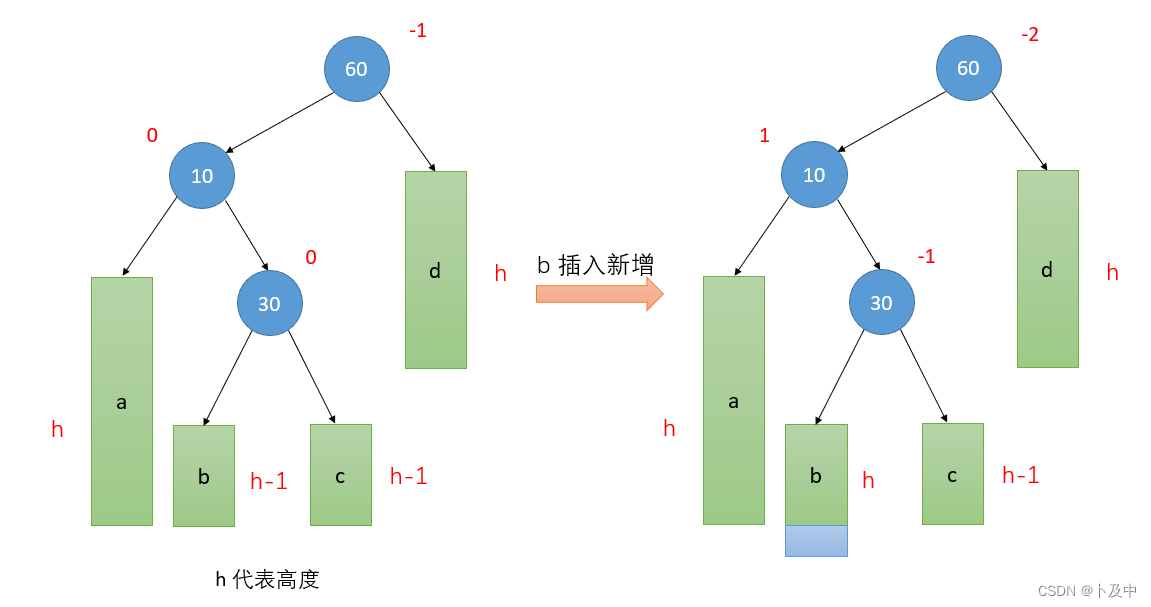
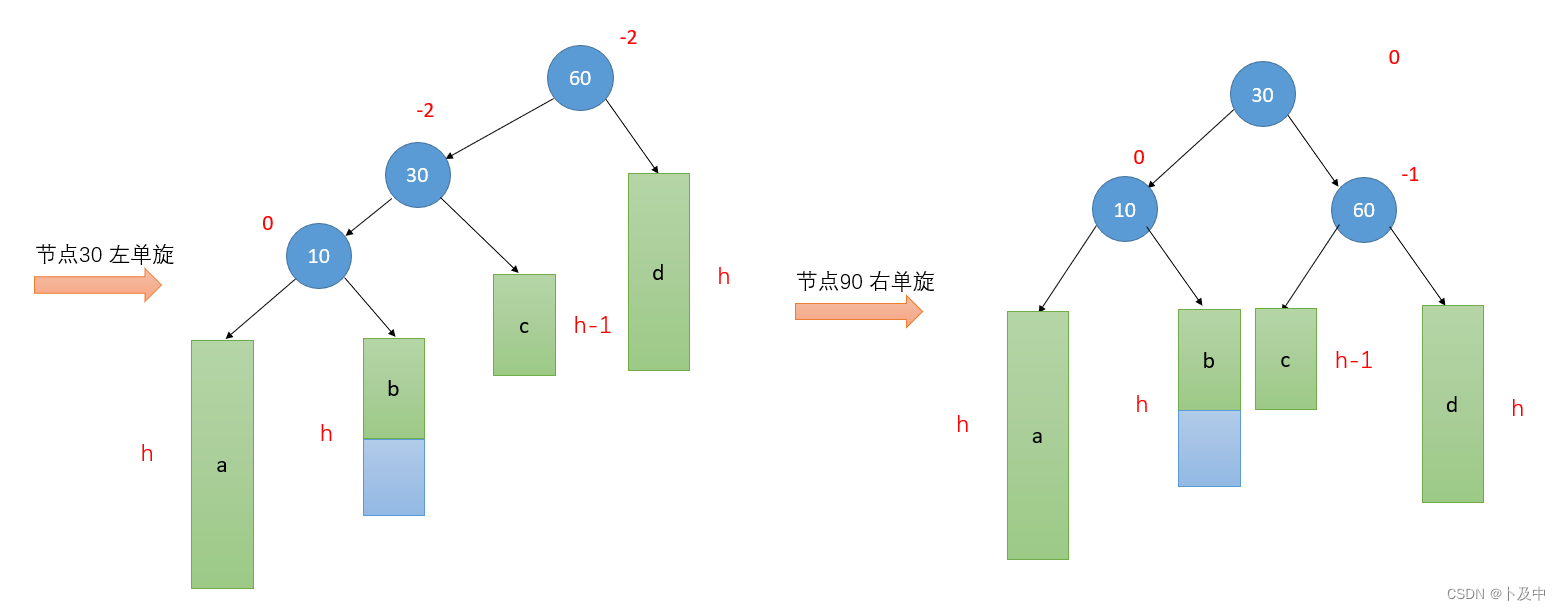
在这里插入图片描述

在这里插入图片描述

  1. 根据图片步骤写代码：定义 subL 和 subLR 分别为 parent 节点的左孩子和右孩子的左孩子。
  2. 对 subL 进行一次左旋操作，此时 subL 变成了 parent 节点的父节点，subLR 成为了 subL 的右孩子。
  3. 对 parent 节点进行一次右旋操作，此时 subLR 节点被转移到 parent 的位置上，并成为 parent 的父节点。同时，subLR 的右子树成为 parent 的左子树，subLR 的左子树成为 subL 的右子树。
  4. 根据新树结构和子树的高度差，调整各个节点的平衡因子。其中，subLR 节点的平衡因子设为 0。如果 subLR 原来的平衡因子为 1，则 parent 的平衡因子、subL 的平衡因子和 subLR 的平衡因子分别设为 0，-1 和 0；如果 subLR 原来的平衡因子为 -1，则三者分别设为 1，0 和 0；如果 subLR 原来的平衡因子为 0，则三者均设为 0。
void RotateLR(Node* parent)
	{
		// 定义subL，subLR
		Node* subL = parent->_left;
		Node* subLR = subL->_right;

		// 保存subLR节点的平衡因子
		int bf = subLR->_bf;

		// 左旋操作，将subLR上移到subL的位置
		RotateL(parent->_left);

		// 右旋操作，将subLR上移到parent的位置
		RotateR(parent);

		// 根据新树结构和子树高度调整各个节点平衡因子
		subLR->_bf = 0; // subLR的平衡因子设为0

		if (bf == 1) // 如果subLR原来的平衡因子为1
		{
			parent->_bf = 1;
			subL->_bf = 0;
		}
		else if (bf == -1)
		{
			parent->_bf = 0;
			subL->_bf = 1;
		}
		else if (bf == 0)
		{
			parent->_bf = 0;
			subL->_bf = 0;
		}
		// subLR的平衡因子取值范围应该是-1，0，1三个值，如果不在这个范围内则代表程序出现了错误
		else
		{
			assert(false); // 断言，程序错误
		}
	}

右左双旋

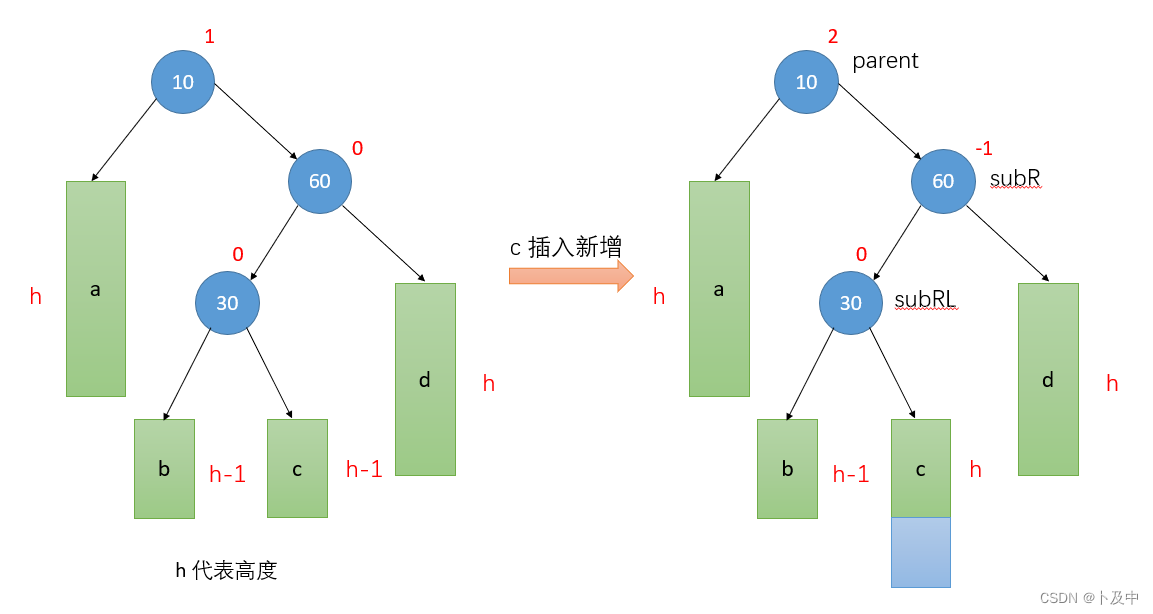
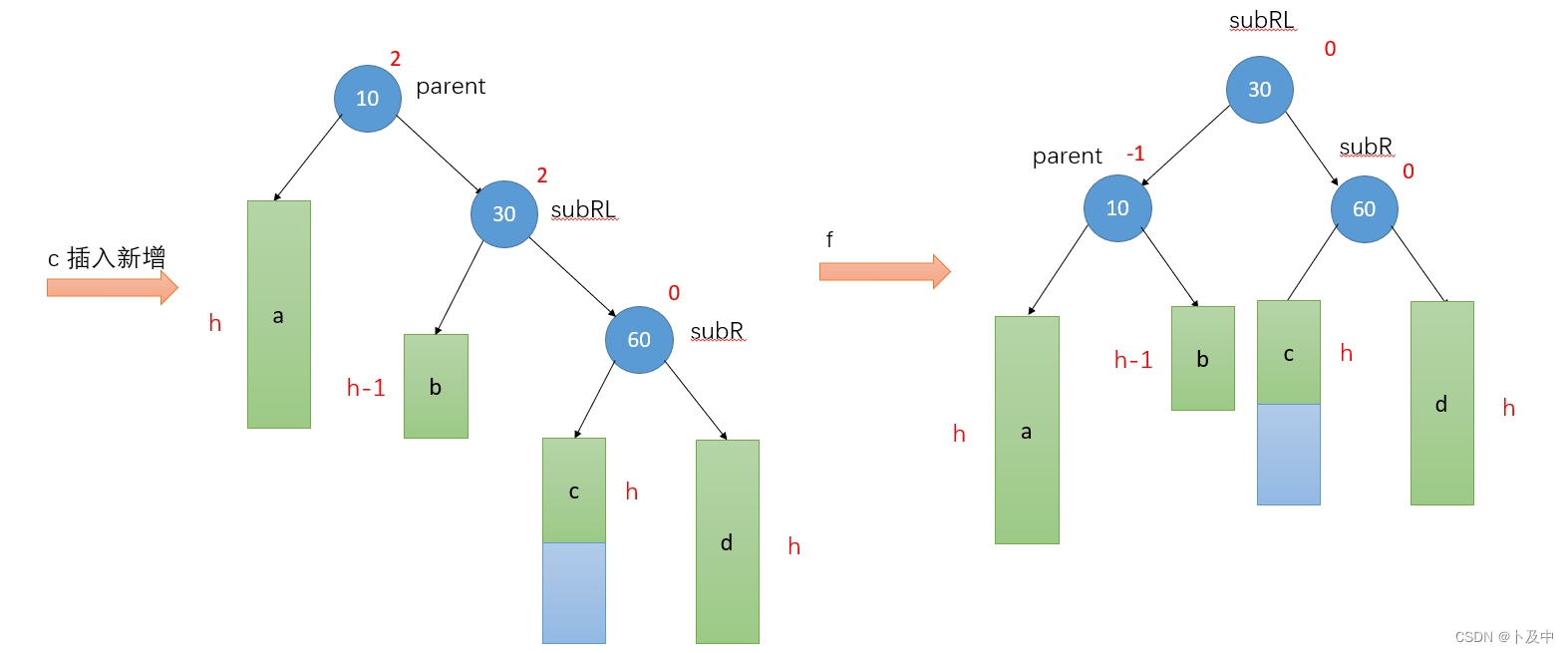
在这里插入图片描述
在这里插入图片描述

  1. 根据图步骤来实现代码：定义 subR 和 subRL 分别为 parent 节点的右孩子和左孩子的右孩子。
  2. 对 subR 进行一次右旋操作，此时 subR 变成了 parent 节点的父节点，subRL 成为了 subR 的左孩子。
  3. 对 parent 节点进行一次左旋操作，此时 subRL 节点被转移到 parent 的位置上，并成为 parent 的父节点。同时，subRL 的左子树成为 parent 的右子树，subRL 的右子树成为 subR 的左子树。
  4. 根据新树结构和子树的高度差，调整各个节点的平衡因子。
void RotateRL(Node* parent)
	{
		// 定义subR，subRL
		Node* subR = parent->_right;
		Node* subRL = parent->_left;

		// 保存subRL节点的平衡因子
		int bf = subRL->_bf;

		// 右旋操作，将subR上移到parent的位置
		RotateR(parent->_right);

		// 左旋操作，将subRL上移到parent的位置
		RotateL(parent);

		// 根据新树结构和子树高度调整各个节点平衡因子
		subRL->_bf = 0; // subRL的平衡因子设为0

		if (bf == 1) // 如果subRL原来的平衡因子为1
		{
			subR->_bf = 0; 
			parent->_bf = -1; 
		}
		else if (bf == -1) 
		{
			subR->_bf = 1; 
			parent->_bf = 0; 
		}
		else if (bf == 0) 
		{
			subR->_bf = 0; 
			parent->_bf = 0;
		}
		// subRL的平衡因子取值范围应该是-1，0，1三个值，如果不在这个范围内则代表程序出现了错误
		else
		{
			assert(false);
		}
	}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/574959.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

初学Qt(Day04)

初学Qt(Day04)

今日目标 创建一个类似游戏手柄的窗口&#xff0c;每次鼠标点击拖动手柄&#xff0c;在qt开发界面输出坐标&#xff0c;每当松开鼠标&#xff0c;手柄自动复位。 目标是实现类似下面这种 先说结论&#xff08;免得我又忘记了&#xff09;&#xff1a;没写完&#xff0c;是一…
阅读更多...
Makefile基础教学（include的使用方法）

Makefile基础教学（include的使用方法）

文章目录 前言一、include在makefile中的概念介绍二、include使用示例三、include中需要注意的一些操作1. 在include前加-选项2. include触发规则创建了文件会发生什么3. include包含的文件夹存在 总结 前言 本篇文章将讲解include的使用方法&#xff0c;在C语言中使用include…
阅读更多...
chatgpt赋能python：Python与SEO的奇妙关系

chatgpt赋能python：Python与SEO的奇妙关系

Python与SEO的奇妙关系 SEO(Search Engine Optimization)&#xff0c;中文翻译为搜索引擎优化&#xff0c;是指通过对网站进行各种技术和内容方面的优化&#xff0c;来提升网站在搜索引擎自然排名中的位置&#xff0c;进而吸引更多的潜在客户。而Python语言&#xff0c;则成为…
阅读更多...
jQuery-attr()、val()、add()属性和each函数

jQuery-attr()、val()、add()属性和each函数

<!DOCTYPE HTML> <html> <head> <meta http-equiv"Content-Type" content"text/html; charsetUTF-8"> <title>jQuery-attr()、add()属性和each函数</title> <script type"text/j…
阅读更多...
[数据集][目标检测]数据集VOC格式绝缘子缺陷检测数据集VOC-4086张

[数据集][目标检测]数据集VOC格式绝缘子缺陷检测数据集VOC-4086张

数据集格式&#xff1a;Pascal VOC格式(不包含分割路径的txt文件和yolo格式的txt文件&#xff0c;仅仅包含jpg图片和对应的xml) 图片数量(jpg文件个数)&#xff1a;4086 标注数量(xml文件个数)&#xff1a;4086 标注类别数&#xff1a;3 标注类别名称:["jueyuanzi",&…
阅读更多...
25 VueComponent 的生命周期

25 VueComponent 的生命周期

前言 这是最近的碰到的那个 和响应式相关的问题 特定的操作之后响应式对象不“响应“了 引起的一系列的文章 主要记录的是 vue 的相关实现机制 呵呵 理解本文需要 vue 的使用基础, js 的使用基础 测试用例 测试用例如下, 一个简单的 按钮事件的触发 问题的调试 这里…
阅读更多...
Linux——网络套接字3|Tcp客户端编写②

Linux——网络套接字3|Tcp客户端编写②

根据我们前面写的服务器，server端需要绑定，而client要不要bind呢？ 不需要，因为客户端一旦和一个非常具体的端口号绑定，可能会导致端口号绑定多个客户端，因此可能会出现某个客户端无法启动。而服务器需要明确的端口号，因为服务器面对的是众多的客户端，服务器端口号一旦被…
阅读更多...
c++ 11标准模板（STL） std::map(五）

c++ 11标准模板（STL） std::map(五）

定义于头文件<map> template< class Key, class T, class Compare std::less<Key>, class Allocator std::allocator<std::pair<const Key, T> > > class map;(1)namespace pmr { template <class Key, class T, clas…
阅读更多...
ros学习

ros学习

1创建工作空间 catkin_init_workspace 将文件夹初始化成ros文件 编译工作空间catkin_make vi ~/.bashrc 加入环境变量bashrc一下在任何终端都生效 catkin_create_pkg learning_communication通讯机制 std_msgs数据结构 rospy roscpp catkin_create_pkg mbot_description ur…
阅读更多...
雅思备考经验！阅读 8.5，听力 8.5！

雅思备考经验！阅读 8.5，听力 8.5！

成绩单 先上热乎乎的成绩单截图&#xff08;2023.5.19 考试&#xff09;&#xff0c;偏科选手出来挨打&#xff01;好在小分都达到了要求~ 英语基础 大概是两三年前考过托福和 GRE&#xff0c;成绩过期了没办法&#xff0c;只能重考&#xff0c;这次试试雅思。 雅思和托福的…
阅读更多...
14-Vue技术栈之Vue3快速上手

14-Vue技术栈之Vue3快速上手

目录 1.Vue3简介2. Vue3带来了什么2.1 性能的提升2.2 源码的升级2.3 拥抱TypeScript2.4 新的特性 1、海贼王&#xff0c;我当定了&#xff01;——路飞 2、人&#xff0c;最重要的是“心”啊&#xff01;——山治 3、如果放弃&#xff0c;我将终身遗憾。——路飞 4、人的梦想是…
阅读更多...
【软考系统规划与管理师笔记】第3篇 信息技术知识2

【软考系统规划与管理师笔记】第3篇 信息技术知识2

目录 1 计算机网络 1.1网络技术标准、协议与应用 Internet技术及应用 2 标识技术 域名系统和统一资源定位器 3 网络分类、组网和接入技术 3.1 网络分类 3.2 网络交换技术 3.3 网络接入技术 3.4 无线网络技术 4 网络服务器和网络存储技术 4.1 服务器 4.2 网络存储技…
阅读更多...
24 memcmp 的调试

24 memcmp 的调试

前言 同样是一个 很常用的 glibc 库函数 不管是 用户业务代码 还是 很多类库的代码, 基本上都会用到 内存数据的比较 不过 我们这里是从 具体的实现 来看一下 它的实现 主要是使用 汇编 来进行实现的, 因此 理解需要一定的基础 测试用例 就是简单的使用了一下 memcpy,…
阅读更多...
【Python】正则表达式应用

【Python】正则表达式应用

知识目录 一、写在前面✨二、姓名检查三、解析电影排行榜四、总结撒花&#x1f60a; 一、写在前面✨ 大家好&#xff01;我是初心&#xff0c;希望我们一路走来能坚守初心&#xff01; 今天跟大家分享的文章是 正则表达式的应用 &#xff0c;希望能帮助到大家&#xff01;本篇…
阅读更多...
Makefile基础教程（路径搜索）

Makefile基础教程（路径搜索）

文章目录 前言一、常用的源码管理方式二、VPATH和vpath1.VPATH2.vpath3.VPATH和vpath优缺点对比 三、VPATH和vpath同时出现make会怎么处理四、vpath指定多个文件夹总结 前言 在前面的文章中我们的文件全部都是放在同一个目录下面的&#xff0c;那么在实际的工程开发中会这样做…
阅读更多...
阿里云服务器备份到本地 镜像 快照 OSS存储 （保姆级图文）

阿里云服务器备份到本地 镜像 快照 OSS存储 （保姆级图文）

目录 省钱措施1. 创建自定义镜像2. 导出镜像创建/选择OSS对象存储空间 3. 下载到本地总结 欢迎关注 『发现你走远了』 博客&#xff0c;持续更新中 欢迎关注 『发现你走远了』 博客&#xff0c;持续更新中 阿里云的这个官方步骤要收几毛钱的费用 因为他要求必须先快照镜像&…
阅读更多...
通过一个平面几何题来梳理解题模型

通过一个平面几何题来梳理解题模型

昨天一位邻居在群里问了一道题目&#xff1a; 已知&#xff1a;如图&#xff0c;OA平分∠BAC&#xff0c;∠1∠2&#xff0e;求证&#xff1a;△ABC是等腰三角形&#xff0e; 先不讲如何来解答这个题目&#xff0c;重点是我们来分析这道题到底在考察什么&#xff0c;如果条件换…
阅读更多...
使用ScreenToGif录制GIF动态图

使用ScreenToGif录制GIF动态图

文章目录 1.下载ScreenToGif工具2. 下载后双击下面的.msi文件进行安装3. 在编辑器中可以对所有帧添加文字描述 1.下载ScreenToGif工具 链接&#xff1a;https://pan.baidu.com/s/1rvFZSbMdNus90hbzxsJlGA 提取码&#xff1a;gyqe2. 下载后双击下面的.msi文件进行安装 按照默认…
阅读更多...
springboot高校专业招生信息管理系统jsp001

springboot高校专业招生信息管理系统jsp001

对于学校来说&#xff0c;每年的学生越来越多&#xff0c;需要管理的专业也有很多&#xff0c;每次专业报名信息的统计工作就变得非常的多&#xff0c;对于报名的统计工作变得非常的复杂。进入二十一世纪后&#xff0c;各种科学技术发速发展&#xff0c;管理软件尤其明显&#…
阅读更多...
Golang每日一练(leetDay0078) 存在重复元素 II\III ContainsDuplicate

Golang每日一练(leetDay0078) 存在重复元素 II\III ContainsDuplicate

目录 219. 存在重复元素 II Contains Duplicate ii &#x1f31f; 220. 存在重复元素 III Contains Duplicate iii &#x1f31f;&#x1f31f;&#x1f31f; &#x1f31f; 每日一练刷题专栏 &#x1f31f; Rust每日一练 专栏 Golang每日一练 专栏 Python每日一练 专栏…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023