部分数据来源:ChatGPT
数据结构
在计算机科学中,数据结构指的是计算机中用来存储和组织数据的方式。数据结构是为算法服务的,同一个算法在不同的数据结构上运行效率可能会有很大的不同。这就要求我们在解决问题时要根据具体情况选择合适的数据结构。
数组
数组是一种线性表数据结构,它能够以连续的内存空间存储同一类型的数据。在 Python 中,数组可以使用列表来实现,例如下面的代码定义了一个整型数组:
arr = [1, 2, 3, 4, 5]数组的访问和赋值操作非常高效,时间复杂度为 O(1),因为可以直接通过下标访问元素。我们可以通过以下代码检验:
print(arr[2]) # 输出 3
arr[2] = 6
print(arr) # 输出 [1, 2, 6, 4, 5]
链表
链表是一种线性表数据结构,它不要求必须存在连续的内存空间来存储数据。链表由节点组成,每个节点中储存了下一个节点的地址。在 Python 中,链表可以使用类来实现,例如下面的代码定义了一个简单的链表:
# 定义链表的每个节点
class ListNode:
def __init__(self, val=0, next=None):
# val表示该节点的值,next指向下一个节点
self.val = val
self.next = next
# 创建链表
head = ListNode(1) # 第一个节点的值是1
head.next = ListNode(2) # 在第一个节点后创建第二个节点,赋值为2
head.next.next = ListNode(3) # 在第二个节点后创建第三个节点,赋值为3
链表的插入和删除操作非常高效,时间复杂度为 O(1),但访问元素时需要从头节点开始遍历,时间复杂度为 O(n)。我们可以通过以下代码检验:
"""
p = head 表示将指针p指向链表的头结点,然后开始遍历链表。
当p不为None时,说明当前节点存在,可以访问它的值并打印出来,
然后将指针p指向下一个节点p.next,继续遍遍历。当p为None时,
说明已经遍历到了链表的末尾,结束循环。
"""
p = head
while p != None: # 使用while循环对链表进行遍历,直到节点为None停止循环
print(p.val)
p = p.next # 将指针p指向下一个节点p.next,继续遍历
输出:
栈
栈是一种具有 LIFO(Last In First Out)特性的数据结构,它的插入和删除操作只能在栈顶进行。在 Python 中,栈可以使用列表来实现,例如下面的代码定义了一个整型栈:
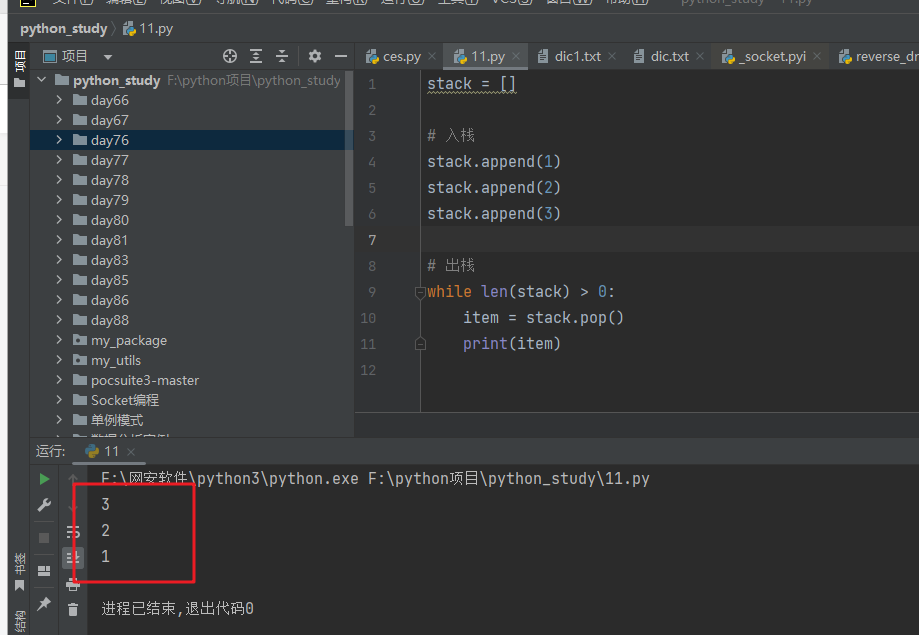
stack = []
# 入栈
stack.append(1) # append(x): 将元素x添加到列表的末尾
stack.append(2)
stack.append(3)
# 出栈
while len(stack) > 0:
item = stack.pop() # pop(x): 弹出列表中下标为x的元素(如果省略x,默认弹出最后一个元素),并返回该元素的值
print(item)
栈的插入和删除操作非常高效,时间复杂度为 O(1)。
输出:栈的特点就是先进后出
队列
队列是一种具有 FIFO(First In First Out)特性的数据结构,它的插入操作只能在队尾进行,删除操作只能在队头进行。在 Python 中,队列可以使用列表来实现,例如下面的代码定义了一个整型队列:
# 定义空的队列,用于存储数据
queue = []
# 入队:将数据添加到队列中,类似于入队操作
queue.append(1) # append(x): 将元素x添加到列表的末尾
queue.append(2)
queue.append(3)
# 出队:从队列中取出数据,类似于出队操作
while len(queue) > 0:
# 取队列的第一个元素
item = queue.pop(0) # pop(x): 弹出列表中下标为x的元素(如果省略x,默认弹出最后一个元素),并返回该元素的值
# 输出该元素的值
print(item)
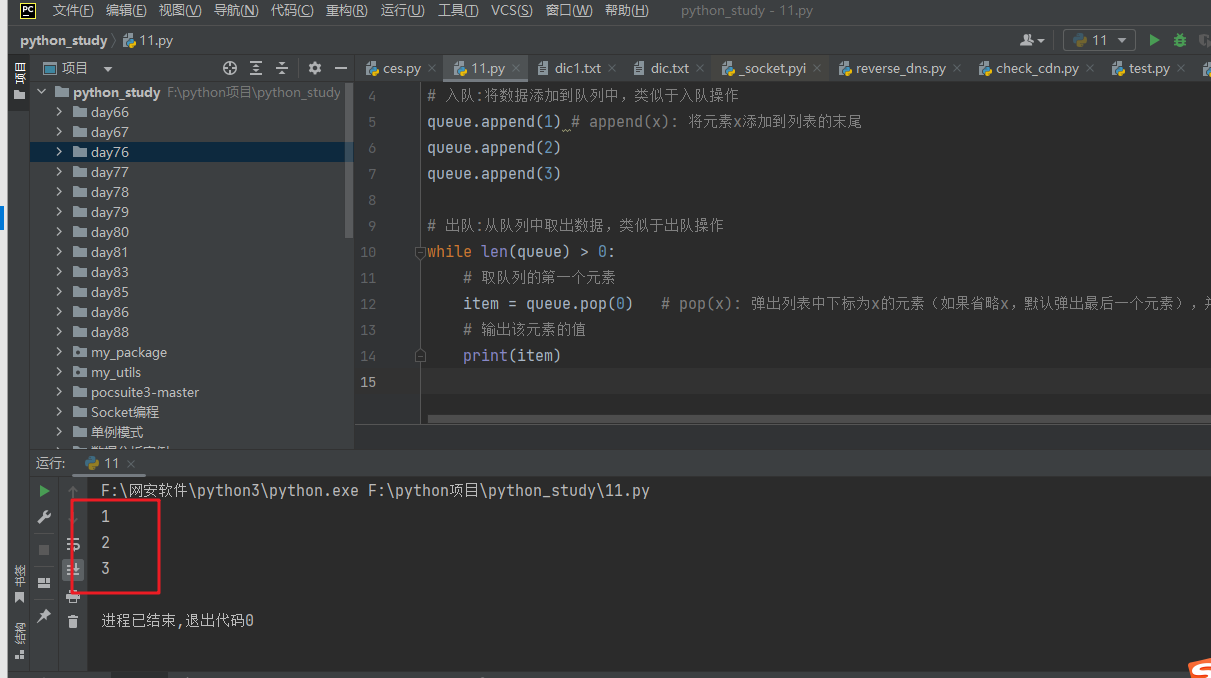
队列的插入和删除操作非常高效,时间复杂度为 O(1)。
输出:队列的特点就是先进先出
树
树是一种非线性数据结构,它由节点和边组成,每个节点储存了一个数据元素和多个子节点。在 Python 中,树可以使用类来实现,例如下面的代码定义了一个简单的二叉树:
# 定义二叉树结构
class TreeNode:
# 二叉树节点初始化方法,参数分别是节点值,左子树,右子树
def __init__(self, val=0, left=None, right=None):
self.val = val # 节点值
self.left = left # 左子树节点
self.right = right # 右子树节点
"""
图示:
+-------------+
| TreeNode |
+-------------+
| val |
| left |
| right |
+-------------+
"""
# 创建二叉树
root = TreeNode(1)
root.left = TreeNode(2)
root.right = TreeNode(3)
"""
图示:
1
/ \
2 3
"""树的插入和删除操作需要考虑节点的位置和旋转操作,时间复杂度通常为 O(log n),
其中 n 表示树中节点的个数。我们可以通过以下代码检验:
# 定义遍历函数
def traverse(root):
# 如果当前节点为空,返回
if root is None:
return
# 输出当前节点的值
print(root.val)
# 递归遍历左子树
traverse(root.left)
# 递归遍历右子树
traverse(root.right)
# 调用遍历函数遍历整棵树,输出节点值
traverse(root) # 输出 1 2 3图
图是一种非线性数据结构,它由节点和边组成,每个节点之间可以有多个边相连。在 Python 中,图可以使用字典来表示,例如下面的代码表示了一个简单的图:
# 定义一个图
graph = {
'A': {'B', 'C'},
'B': {'D', 'E'},
'C': {'F'},
'D': set(), # set() 表示一个空集合,即一个不包含任何元素的集合。
'E': {'F'},
'F': set()
}
其中,字典的键表示节点,值则表示与该节点相邻的节点。
图的遍历和搜索操作较为复杂,常用的算法包括深度优先搜索(DFS)和广度优先搜索(BFS)。我们可以通过以下代码检验 DFS 的实现:
# 使用深度优先遍历(DFS)按照字典序访问图中的节点
def dfs(graph, start, visited=set()):
visited.add(start) # 将节点标记为已访问
print(start) # 打印已访问的节点
for next_node in graph[start]: # 遍历该节点的所有邻接节点
# 如果邻接节点未被访问,则跳转到该节点并递归执行DFS
if next_node not in visited:
dfs(graph, next_node, visited)
# 从A节点开始深度优先遍历图
dfs(graph, 'A') # 输出 A B D E F C算法
算法是解决特定问题的一系列指令或操作步骤,它不仅需要解决问题,还需要解决问题的效率。常见的算法包括排序、搜索、字符串匹配等。
排序
排序是对数据进行按照某种规则进行排序的操作。常见的排序算法包括冒泡排序、插入排序、快速排序、归并排序等。我们可以通过以下代码检验快速排序的实现:
# 定义快速排序函数 quick_sort
def quick_sort(arr):
# 当传入的数组 arr 长度小于等于 1 时,直接返回该数组
if len(arr) <= 1:
return arr
# 选取数组 arr 的最后一个元素为 pivot(基准)值
pivot = arr.pop()
# 定义两个列表,分别用来存放小于和大于等于 pivot 值的元素
left_list = []
right_list = []
# 遍历数组 arr 中的每个元素,并将其添加到 left_list 或 right_list 中
for i in arr:
if i < pivot:
left_list.append(i) # 小于 pivot 的元素添加到 left_list 中
else:
right_list.append(i) # 大于等于 pivot 的元素添加到 right_list 中
# 对 left_list 和 right_list 分别递归调用快速排序函数,并将排序结果和 pivot 值合并返回
return quick_sort(left_list) + [pivot] + quick_sort(right_list)
# 调用快速排序函数对数组 arr 进行排序
arr = [3, 2, 1, 5, 4]
sorted_arr = quick_sort(arr)
print(sorted_arr) # 输出 [1, 2, 3, 4, 5]搜索
搜索是从某个集合中找到其子集中满足一定条件的元素的操作。常见的搜索算法包括深度优先搜索(DFS)和广度优先搜索(BFS)。我们可以通过以下代码检验 DFS 的实现:
# 定义广度优先搜索函数 bfs,用于搜索从 start 到 end 的路径
def bfs(graph, start, end):
# 定义一个队列,用于存放待遍历节点,初始值为起点 start,路径为[start](一个只包含 start 的列表)
queue = [(start, [start])]
# 对未遍历完的节点进行遍历
while queue:
# 从队列的头部取出节点和路径
(node, path) = queue.pop(0)
# 遍历当前节点的邻近节点,即下一个节点
for next_node in graph[node] - set(path):
# 如果下一个节点是终点 end,则返回路径 path + [next_node],即起点 start 到终点 end 的完整路径
if next_node == end:
return path + [next_node]
else:
# 如果下一个节点不是终点 end,则将该节点添加到队列中,并将新路径 path + [next_node] 传递给该节点
queue.append((next_node, path + [next_node]))
# 定义一个有向图 graph
graph = {
'A': {'B', 'C'},
'B': {'D', 'E'},
'C': {'F'},
'D': set(),
'E': {'F'},
'F': set()
}
# 调用广度优先搜索函数 bfs 查找从节点 A 到节点 F 的路径
path = bfs(graph, 'A', 'F')
print(path) # 输出 ['A', 'C', 'F']字符串匹配
字符串匹配是在现有字符串中查找另一个字符串或者模式的过程。常见的字符串匹配算法包括暴力匹配、KMP 算法、Boyer-Moore 等。这里我们可以通过以下代码检验暴力匹配的实现:
# 定义暴力匹配函数 brute_force_match,用于在主串 main_str 中找到模式串 pattern 的位置
def brute_force_match(main_str, pattern):
n = len(main_str) # 计算主串 main_str 的长度
m = len(pattern) # 计算模式串 pattern 的长度
for i in range(n - m + 1): # 遍历主串中所有可能的起始位置
j = 0
# 从当前位置 i 开始,逐个比较主串和模式串中的字符
while j < m and main_str[i + j] == pattern[j]:
j += 1
# 如果模式串中的所有字符都匹配成功,则返回在主串中的起始位置 i
if j == m:
return i
# 如果在主串中找不到模式串,则返回 -1
return -1
# 测试暴力匹配函数 brute_force_match
main_str = 'abcdabccd'
pattern = 'abcc'
match_index = brute_force_match(main_str, pattern)
print(match_index) # 输出 4 暴力匹配,即朴素字符串匹配算法,是一种简单直观的串匹配算法,也是所有模式匹配算法中最基本的算法。它的基本思想是逐个比较主串中的每个字符和模式串中的字符是否匹配。在暴力匹配函数 brute_force_match() 中,首先计算主串 main_str 和模式串 pattern 的长度,然后遍历主串中所有可能的起始位置,从当前位置 i 开始逐个比较主串和模式串中的字符,如果模式串中的所有字符都匹配成功,则返回在主串中的起始位置 i,否则继续查找。当查找结束后仍未找到匹配的字符串,则返回 -1。
总结
本文介绍了数据结构和算法的概念,并且给出了 Python 中常用的数据结构和算法的实现示例。在实际开发中,合理地选择数据结构和算法,能够大大提高代码效率和性能,同时也能够提高我们的编程能力。相信通过学习本文,大家对数据结构和算法有了更深入的了解,也掌握了常用算法在 Python 中的实现方式。






![[组合数学] 容斥原理polya定理](https://img-blog.csdnimg.cn/75e0ea7afd9e43268795a0ed39101f7c.png)