目录
- 什么是堆?
- 堆的分类
- 堆的实现
- 堆排序——时间复杂度(N*logN)
- TopK问题
什么是堆?
什么是堆?
堆是一种叫做完全二叉树的数据结构,分为大根堆和小堆,堆排序也是基于这种结构产生的。
堆是父亲节点和孩子节点之间的关系。
堆的分类
**大根堆:**树任何一个父亲节点的值都大于或等于孩子。
**小根堆:**树任何一个父亲节点的值都小于或者等于孩子。
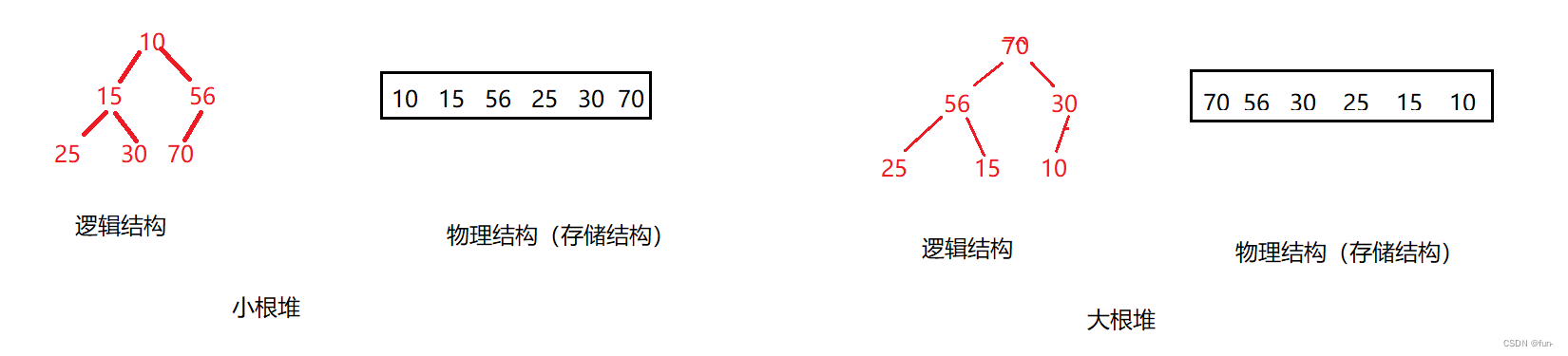
堆的逻辑结构是一棵二叉树,物理结构是一维数组,只要是数组就可以看成是一棵完全二叉树。
堆不一定有序
堆的实现
1、堆的结构 堆的初始化和堆的销毁(动态)
我们前面提到堆的存储结构其实是一个数组,所以在堆的结构中,应该定义数组、元素个数和数组容量。
typedef int HPDataType;
typedef struct Heap
{
HPDataType* a;
int size;
int capacity;
}HP;
void HeapInit(HP* php)
{
assert(php);//断空指针
php->a = NULL;
php->size = 0;
php->capacity = 0;
}
void HeapDestroy(HP* php)
{
assert(php);
free(php->a);
php->a = NULL;
php->size = 0;
php->capacity = 0;
}
2、向堆中插入数据
向堆中插入数据,物理上是插入到数组的尾部,空间不够则需要扩容
逻辑上该数据是插入到完全二叉树中。
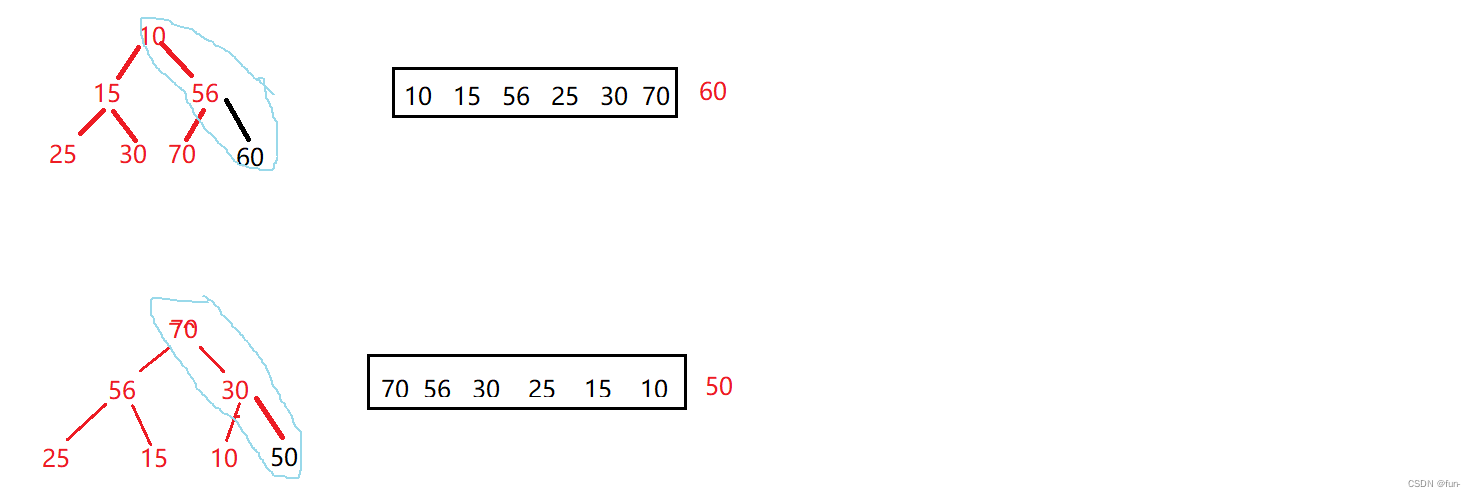
插入该节点后,要继续保持该堆是大根堆或者是小根堆,要对插入节点后的堆进行一些检查和调整。
主要检查的方面在孩子和双亲之间,以保证父亲节点大于孩子节点(大根堆)或者父亲节点小于孩子节点(小根堆)。
这里采用向上调整算法。
向上调整算法:
前提:添加一个数据之前,该堆是大根堆或者是小根堆

主要调整孩子和双亲。堆的物理结构是数组,所以很容易可以得到双亲和孩子的下标:
parent = (child-1) / 2
左孩子:child = 2* parent+1
右孩子:child = 2* parent+2
插入节点形成小根堆
1、在调整孩子和双亲时,如果孩子节点值小于双亲,则调整孩子和双亲节点
2、孩子和父亲节点进行交换
3、继续调整孩子和父亲的下标,继续比较孩子节点是否小于双亲,如果小于则继续上述步骤,如果不小于则证明已经是小根堆,跳出循环。
4、循环结束条件:当孩子节点的下标到根节点时,循环结束。
void Swap(HPDataType* p1, HPDataType* p2)
{
HPDataType tmp = *p1;
*p1 = *p2;
*p2 = tmp;
}
void AdjustUp(int* a, int child)
{
int parent = (child - 1) / 2;
while (child>0)//孩子节点下标大于0才进行向上调整
{
if (a[child] < a[parent])
{
Swap(&a[child], &a[parent]);//交换父亲和孩子节点
child = parent;//继续向上调整
parent = (child - 1) / 2;
}
else
{
break;
}
}
}
void HeapPush(HP* php, HPDataType x)
{
assert(php);
if (php->size == php->capacity)
{
int newcapacity = php->capacity == 0 ? 4 : php->capacity * 2;
HPDataType* tmp = (HPDataType*)realloc(php->a, newcapacity * sizeof(HPDataType));
if (tmp == NULL)
{
perror("realloc fail");
return;
}
php->a = tmp;
php->capacity = newcapacity;
}
//插入数据
php->a[php->size] = x;
php->size++;
AdjustUp(php->a, php->size - 1);//向上调整,从孩子的位置向上调整
}
3、删除堆顶数据
注意:虽然说堆的物理结构是一个数组,但是不能使用挪动删除的方法。
挪动删除不能保证挪动后形成的堆还是有序的(大根堆或者小根堆),挪动后父子关系全乱了。

向下调整算法:
1、假设调小根堆,则从根节点开始调整,调整父节点和其孩子节点
2、如果父亲节点大于孩子节点,则找孩子节点当中最小节点值的孩子节点与父亲节点交换,之后调整父亲节点和孩子节点的下标继续向下调整
3、如果父亲节点小于孩子节点,则满足小根堆的条件,不进行调整。
***前提:***左右子树是大根堆或者小根堆
假设我们要删除堆顶数据:
1、先将堆顶元素和数组最后一个元素进行交换(也就是堆的最后一个元素),删除堆顶元素10

2、使用向下调整算法调小根堆(大根堆)

3、每次调整后都要继续向下调整(改变孩子和父亲的下标)
注意:
1、循环结束的条件:每次向下调整都要保证孩子的坐标在数组的范围之内。
2、左孩子存在但是右孩子不一定存在,所以一定要在右孩子存在的情况下,再进行右孩子和左孩子的大小比较
//从父亲(根节点)开始向下调整
void AdjustDown(int* a, int n, int parent)
{
int child = 2 * parent + 1;//假设左孩子最小
while (child<n)
{
if (a[child + 1] < a[child])//如果右孩子比左孩子更小
{
child++;//则最小的孩子+1变成右孩子
}
if (child+1<n && a[child] < a[parent])
{
Swap(&a[child], &a[parent]);
parent = child;
child = 2 * parent + 1;
}
else
{
break;
}
}
}
void HeapPop(HP* php)
{
assert(php);
assert(php->size > 0);
//交换并删除堆顶元素
Swap(&php->a[0], &php->a[php->size - 1]);
php->size--;
//向下调整成小根堆(大根堆)
AdjustDown(php->a, php->size, 0);
}
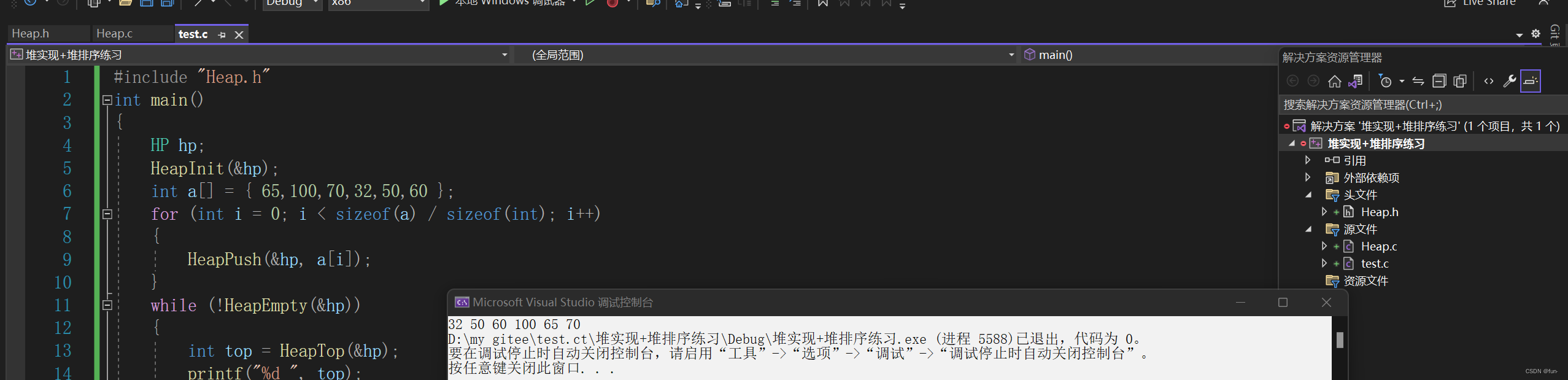
**注意:**我们可以看到屏幕的结果是有序的,但是这并不是排序,只是有序打印。
4、取堆顶元素,堆中元素个数,堆的判空
HPDataType HeapTop(HP* php)
{
assert(php);
assert(!HeapEmpty(php));
return php->a[0];
}
int HeapSize(HP* php)
{
assert(php);
return php->size;
}
bool HeapEmpty(HP* php)
{
assert(php);
return php->size == 0;
}
堆排序——时间复杂度(N*logN)
1、可以依次取堆顶元素放回数组
void HeapSort(int* a, int n)
{
HP hp;
HeapInit(&hp);
for (int i = 0; i < n; i++)
{
HeapPush(&hp, a[i]);
}
int i = 0;
while (!HeapEmpty(&hp))
{
int top = HeapTop(&hp);
a[i++] = top;//
HeapPop(&hp);
}
}
int main()
{
int a[] = { 7,8,3,5,1,9,5,4 };
HeapSort(a, sizeof(a) / sizeof(int));
return 0;
}
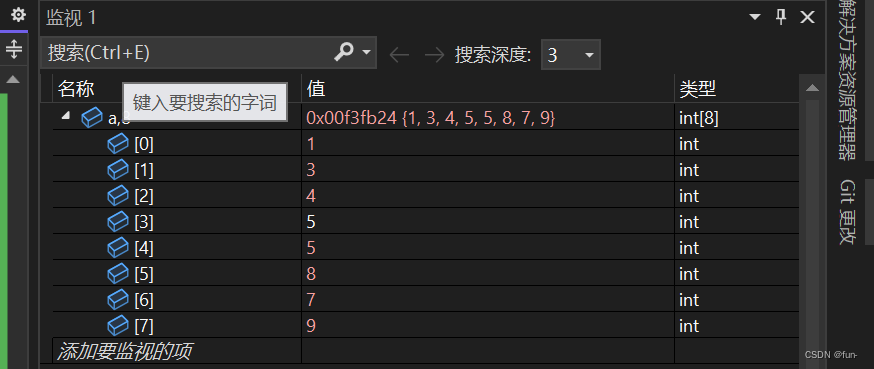
可以排序,但是这不是最佳方法。
此方法的弊端:
1、要先有一个堆——建堆N*logN
2、空间复杂度大
3、要来回拷贝数据很麻烦
2、最佳堆排序方法
1、先建堆——向上调整建堆,模拟插入的过程,每次插入都进行一次调整

2、升序:建大堆
降序:建小堆
降序:建小堆
1、建小堆选出最小的,首尾交换,最小的放到最后的位置
2、把最后一个数据,不看做堆里面的, 向下调整(时间复杂度logN) 选出次小的,再进行交换

向上调整建堆:

注意顺序:先交换堆顶元素和end位置的元素,再进行向下调整,最后end–。
代码:
void HeapSort(int* a, int n)
//向上调整建堆
{
for (int i = 1; i < n; i++)
{
AdjustUp(a, i);
}
int end = n - 1;
while (end>0)
{
Swap(&a[0], &a[end]);
//再调整,选出次小的数
AdjustDown(a, end, 0);
end--;
}
}
int main()
{
int a[] = { 7,8,3,5,1,9,5,4 };
HeapSort(a, sizeof(a) / sizeof(int));
return 0;
}
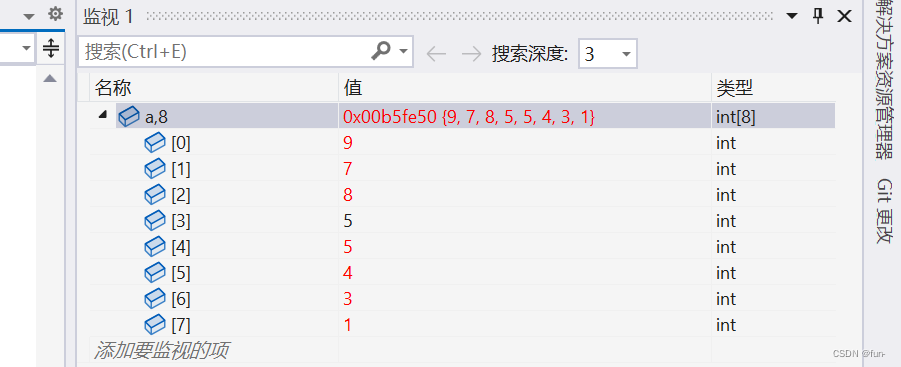
从叶子节点的父亲节点开始向下调整建堆:

void HeapSort(int* a, int n)
//向上调整建堆
{
/*for (int i = 1; i < n; i++)
{
AdjustUp(a, i);
}*/
for (int i = (n - 1 - 1) / 2; i >= 0; i--)
{
AdjustDown(a, n, i);
}
int end = n - 1;
while (end>0)
{
Swap(&a[0], &a[end]);
//再调整,选出次小的数
AdjustDown(a, end, 0);
end--;
}
}
int main()
{
int a[] = { 7,8,3,5,1,9,5,4 };
HeapSort(a, sizeof(a) / sizeof(int));
return 0;
}
综合比较使用向下调整建堆会比使用向上调整建堆的方法更快
TopK问题
TopK问题实际应用:
1、饿了么、美团美食门店排行榜
2、优质筛选问题
3、专业前10名
4、世界500强
…
TopK问题方法1:
将给定的N个数建成大堆,再Pop K次,就可以找出最大的前K个
(但是如果N非常大,这种方法就解决不了)
TopK问题最优思路:
1、建立K个数的小堆
2、后面N-K个数,依次比较,如果比堆顶的数据大,就替换他进堆(覆盖堆顶元素进行向下调整)
3、最后这个小堆的值就是TopK
Step1:造数据
打开文件,向文件中写入1000000个数据
void CreateData()
{
int n = 1000;//数据个数
srand(time(0));
const char* file = "data.txt";
FILE* fin = fopen(file, "w");
if (fin == NULL)
{
perror("fopen errror");
return;
}
for (size_t i = 0; i < n; i++)
{
int x = rand() % 1000000;
fprintf(fin, "%d ", x);
}
fclose(fin);
}
int main()
{
CreateData();
return 0;
}

void CreateData()
{
int n = 10000;//数据个数
srand(time(0));
const char* file = "data.txt";
FILE* fin = fopen(file, "w");
if (fin == NULL)
{
perror("fopen error");
return;
}
for (size_t i = 0; i < n; i++)
{
int x = rand() % 1000000;
fprintf(fin, "%d\n ", x);
}
fclose(fin);
}
void PrintTopK(int k)
{
const char* file = "data.txt";
FILE* fout = fopen(file, "r");
if (fout == NULL)
{
perror("fopen error");
return;
}
int* kminheap = (int*)malloc(sizeof(int) * k);//K个数的小堆
if (kminheap == NULL)
{
perror("malloc error");
return;
}
for (int i = 0; i < k; i++)
{
fscanf(fout, "%d", &kminheap[i]);//读前k个
}
//向下调整建小堆
for (int i = (k - 1 - 1) / 2; i >= 0; i--)
{
AdjustDown(kminheap, k, i);
}
int val = 0;
while (!feof(fout))
{
fscanf(fout, "%d", &val);//从k+1开始读
if (val > kminheap[0])
{
kminheap[0] = val;//覆盖
AdjustDown(kminheap, k, 0);
}
}
for (int i = 0; i < k; i++)
{
printf("%d ", kminheap[i]);
}
}
int main()
{
//CreateData();
PrintTopK(5);
return 0;
}