精品题解 👉 《九章刷题录》

📜 目录：

「 法一 」暴力美学

「 法二 」十字分割法

「 法三 」逐行二分

---

JZ4 - 二维数组中的查找

📚 题目描述：在一个二维数组 array 中（每个一维数组的长度相同），每一行都按照从左到右递增的顺序排序，每一列都按照从上到下递增的顺序排序。请完成一个函数，输入这样的一个二维数组和一个整数，判断数组中是否含有该整数。

比如下列二维数组 ，给定 target = 3，则返回 true；给定 target = 7，则返回 false：

int a[3][4] = {{1, 2, 3, 4}, {2, 3, 4, 5}, {3, 4, 5, 6}};  // C

• 数据范围：矩阵的长宽满足  ， 矩阵中的值满足 
• 进阶：时间复杂度 ，空间复杂度 

💭 示例：I/O

输入：7,[[1,2,8,9],[2,4,9,12],[4,7,10,13],[6,8,11,15]]
返回：true
说明：存在7，返回true  

输入：3,[[1,2,8,9],[2,4,9,12],[4,7,10,13],[6,8,11,15]]
返回：false
说明：不存在3，返回false   

输入：3,[[1,2,8,9],[2,4,9,12],[4,7,10,13],[6,8,11,15]]
返回：false
说明：不存在3，返回false   

✅ 模板：C语言

/**
 * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
 *
 * 
 * @param target int整型 
 * @param array int整型二维数组 
 * @param arrayRowLen int array数组行数
 * @param arrayColLen int* array数组列数
 * @return bool布尔型
 */
bool Find(int target, int** array, int arrayRowLen, int* arrayColLen ) {
    // write code here
}

✅ 模板：C++

class Solution {
public:
    bool Find(int target, vector<vector<int> > array) {
    }
};

---

「 法一 」暴力美学

" 别和我说什么二分线性算法，老夫敲代码就是一把梭，直接 for 暴力！ "

💡 思路：既然是要找数组中是否存在某个数字，直接逐行逐列遍历搜索即可。对于二维数组的遍历，需要用两层循环，因此时间复杂度为 ，空间复杂度为 。

💬 代码演示：C语言

#include <stdbool.h>
bool Find(int target, int** array, int arrayRowLen, int* arrayColLen) {
    for (int i = 0; i < arrayRowLen; i++) {        // 遍历行
        for (int j = 0; j < *arrayColLen; j++) {   // 遍历列
            if (array[i][j] == target) {
                return true;   // 找到了
            }
        }
    }
    return false;    // 没找到
}

 我们定义  搜索二维数组，如果找到了目标值则返回 true，如果搜索完仍未找到我们根据题意返回 -1 即可。

---

「 法二 」十字分割法

" 既有规律可循，一次排除一批，岂不美哉？"

💡 思路：题中描述的数组是存在规律的："在一个二维数组 array 中（每个一维数组的长度相同），每一行都按照从左到右递增的顺序排序，每一列都按照从上到下递增的顺序排序。" 这就意味着矩阵内部的行列都是有序，数组右上角的值在这一行中是最大的，而在这一列中是最小的。，每次判断都能剔除一整行或一整列。

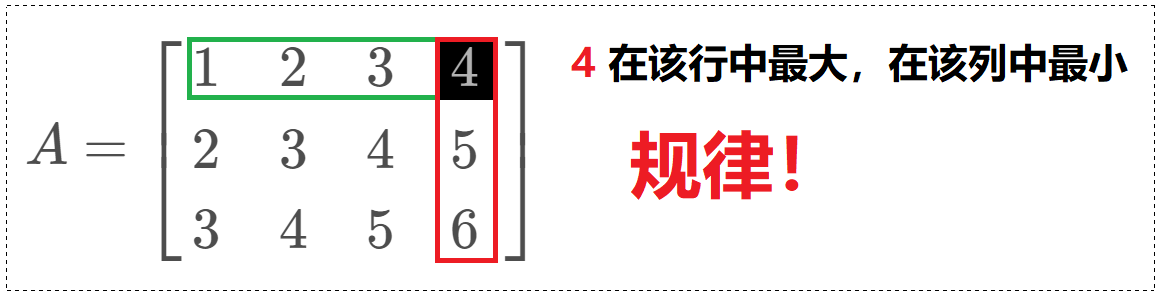
我们思考一个问题 —— "一次排除一个和一次排除一批"，谁的效率更高？当然是后者效率更高！如果按照这个本质，我们在套上我们想到的 「法1」，其本质就是一次排除一个，效率自然也就不能再高了。我们观察这样的数组，我们可以通过比较目标值，和数组中右上角的值（或左下角的值），因为右上角的值是这一行中最大的，是这一列中最小的。

对我们而言，我们可以 直接拿着目标值，和当前矩阵的右上角的值进行比较。 如果当前值比右上角的值小，说明当前你要查找的值是绝对不会出现在这一列的，就可以把这一列整体排除。

现在我们就做到一行排除一行或者一列了。此时我们就需要考虑临界条件的问题，我们要关注什么时候结束，找到了，如果没找到，一定是一个行或者列出现了越界的条件，导致程序退出。排除时，行不断加，列不断减，因此临界条件为：行 (row) 不能增到 arrayRowLen，列 (col) 不能缩到比 0 小。

📚 介绍：上面我们介绍的这种方法，称之为 十字分割法 (Cross-Sectional Search)，是在有序二维数组中查找目标元素的高效算法，当然前提是有序！它利用了有序数组的特性，通过逐步缩小搜索范围来快速确定目标元素的位置。"十字" 也很形象的表现出排除 "每次判断都能剔除一整行或一整列" 的特点。通过不断缩小搜索范围，十字分割法可以快速确定目标元素的位置，从而提高查找的效率。十字分割法的基本步骤如下：

Step1：选择一个起始点，通常是数组的右上角或左下角（个人习惯于右上角）

Step2：将起始点的值与目标元素进行比较。

Step3：如果起始点的值等于目标元素，找到目标元素，搜索结束。

Step4：如果起始点的值大于目标元素，目标元素可能在当前元素的左边或上方，将搜索范围缩小到当前元素的左边区域或上方区域。

Step5：如果起始点的值小于目标元素，目标元素可能在当前元素的右边或下方，将搜索范围缩小到当前元素的右边区域或下方区域。

* 重复步骤 2~5，直到找到目标元素，或达到临界条件（数组不能越界）！

该方法的时间复杂度为  ，其中  为二维数组的行数， 为二维数组的列数。

💬 代码演示：C语言

bool Find(int target, int** array, int arrayRowLen, int* arrayColLen ) {
    int row = 0;                // 当前行
    int col = arrayRowLen - 1;  // 当前列

    while (row < arrayRowLen && col >= 0) {
        // array[row][col] 必定是当前行最大的，当前列最小的
        if (target < array[row][col]) {   // 如果目标值小于右上角
            col--;   // 不可能出现在该列，排除
        }
        else if (target > array[row][col]) {  // 如果目标值大于右上角
            row++;  // 不可能出现在该行，排除
        }
        else {
            return true;   // 找到了
        }
    }
    return false;    // 没找到
}

我们定义 row 和 col，初始化使 array[row][col] 能指向右上角，此时 array[row][col] 必然是当前行最大的，当前列最小的。主要判断目标值和 array[row][col] 的大小，如果比它小，那肯定不会出现在该列，因为垂直往下只会有更大的，所以肯定不在该列，直接 col-- 排除该列。如果比它大。那肯定不会出现在该行，因为横向只有比它还要小的，所以肯定不在该行，直接 row++ 排除该行，走到下一行。如此一来我们搜索的范围越来越小，最后如果有满足 target == array[row][col] 条件的情况就可以返回 true 了，数组都缩没了还没找到那自然是根本不存在目标值，循环外返回 false 即可。至于这里的循环边界的控制，是决定循环什么时候结束的关键！row 作为行，是肯定要比行长度 arrayRowLen 小的，如果 row++ 到 arrayRowLen 这个边界了，就会越界。同样，col-- 到 0 下标时如果在继续减也会越界，所以这里循环控制把控好就行。

时间复杂度为 （R 表示行 C 表示列），空间复杂度为 。

---

「 法三 」逐行二分

" 逐行二分搜之…… "

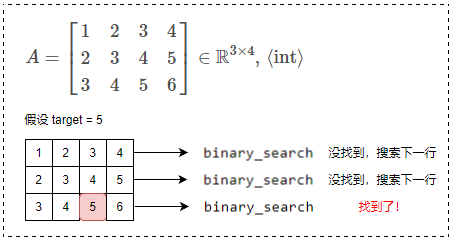
💡 思路：我们可以对数组的每行进行二分查找！手写一个 BinarySearch 函数，然后只需要逐行传递给该函数即可。对数组地每一行使用二分，其时间复杂度为 ，空间复杂度为 。

💬 代码演示：C语言

#include <stdbool.h>
int binary_search(int* arr, int sz, int k) {
    int left = 0;
    int right = sz - 1;
    int mid = 0;

    while (left <= right) {
        mid = (left + right) / 2;
        if (arr[mid] < k) {
            left = mid + 1;
        } 
        else if (arr[mid] > k) {
            right = mid - 1;
        } 
        else {
            return mid;  // 找到了
        }
    }

    return -1;  // 没找到
}

bool Find(int target, int** array, int arrayRowLen, int* arrayColLen ) {
    int ret = 0;   // 用于接收返回值

    // 遍历行，将行依次传给 binary_search 函数
    for (int i = 0; i < arrayRowLen; i++) {
        ret = binary_search(array[i], *arrayColLen, target);
        if (ret != -1) {
            return true;   // 找到了
        }
    }
    return false;
}

我们手动实现好 BinrarySearch 函数后，我们只需要写一个 for 循环，把行依次传入该数组。会先把第一行数组传给该函数，如果找到了就结束了，没找到就继续把下一行传给该函数以此类推……最后如果没有找到根据题意返回 -1 即可。

​

📌 [ 笔者 ]   王亦优
📃 [ 更新 ]   2023.5.24
❌ [ 勘误 ]   /* 暂无 */
📜 [ 声明 ]   由于作者水平有限，本文有错误和不准确之处在所难免，
              本人也很想知道这些错误，恳望读者批评指正！

📜 参考资料  C++reference[EB/OL]. []. http://www.cplusplus.com/reference/. Microsoft. MSDN(Microsoft Developer Network)[EB/OL]. []. . 百度百科[EB/OL]. []. https://baike.baidu.com/. 牛客网. 剑指offer 题解 [EB/OL]. []. https://www.nowcoder.com/exam/oj/ta?tpId=13.