二叉搜索树
二叉树:二叉树每个结点最多有两个子树
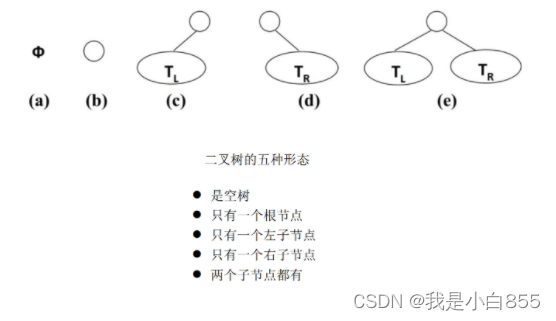
二叉搜索树: (BST) 其实就是在普通的二叉树上加了一些限制
没有任何限制,二叉搜索树插入子结点的时候有一些特殊的要求
二叉搜索树的性质:
- 非空左子树所有的键值小于其根结点的键值
- 非空右子树所有的键值大于其根结点的键值
- 左、右子树本身也都是二叉搜索树
二叉搜索树的特点:相对较小的值总是保存在左子结点,相对较大的值总是保存在右子结点上。
二叉搜索树的遍历:先序遍历、中序遍历、后序遍历。
二叉搜索树的优点:可以快速的找到给定的关键字的数据项,快速的插入和删除数据。
二叉搜索树的缺陷:时间性能上是有局限性。
比较好的二叉搜索树的数据应该是左右分布均匀的。
但是我们在插入连续的数据的时候,会导致数据分布不均匀,不均匀的树我们称为:非平衡树
二叉平衡树
二叉平衡树:平衡二叉搜索树,也叫做AVL树,是一种自平衡的树。除了规定左结点小于根结点,有结点大于根结点以外,还规定了左子树和右子树的高度差不得超过1。
我们需要建立一棵尽可能矮的树平衡因子: 左子树的高度减去其右子树的高度
所以,平衡二叉树中,各个结点的平衡因子的绝对值小于等于1。 [-1,0,1] 。可以满足我们的二叉平衡树的需求,平衡二叉树是一棵二叉搜索树,只不过平衡树比较矮而已。
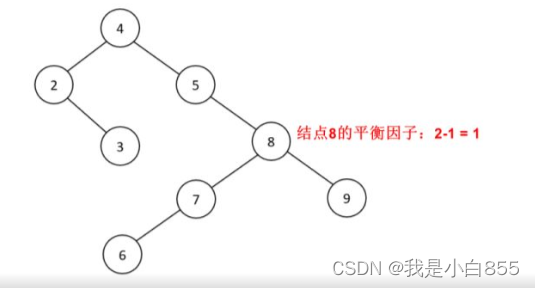
控制平衡因子:如果平衡因子的绝对值超过了1,那么我们就称之为:失衡,结点需要随时添加、随时删除
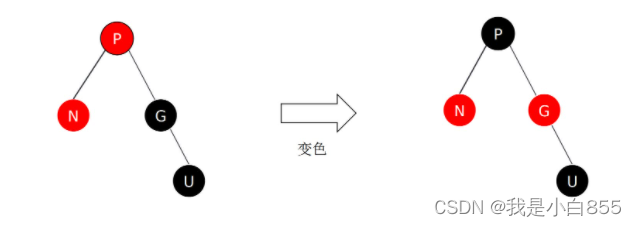
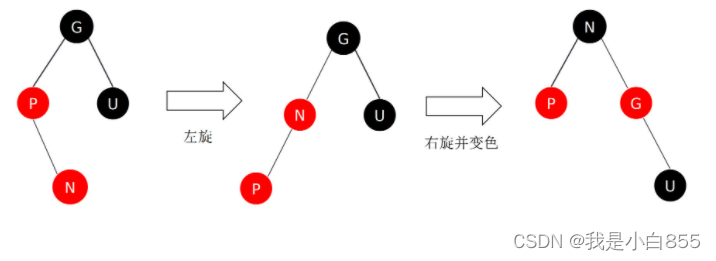
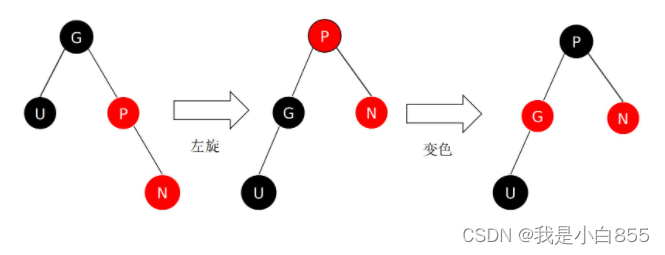
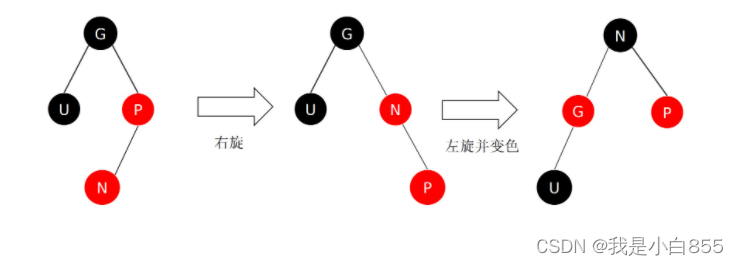
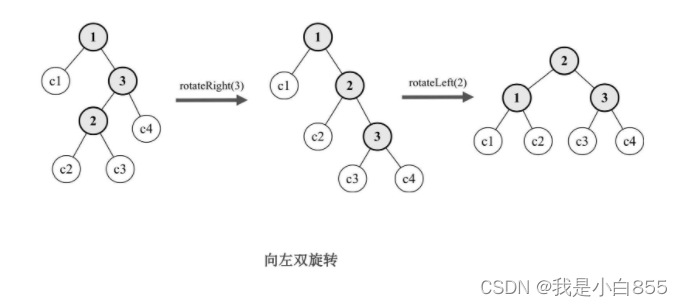
我们插入数据的时候,导致平衡二叉树出现了失衡。控制平衡因子,要把平衡因子控制在绝对值不大于1的范围内(平衡调整),在平衡二叉树中,使用旋转换作来达到平衡。
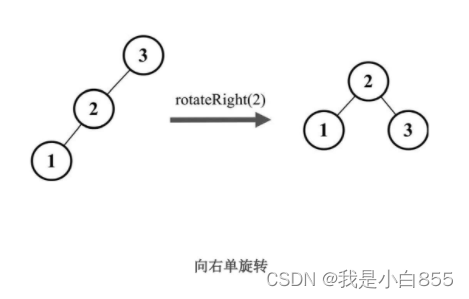
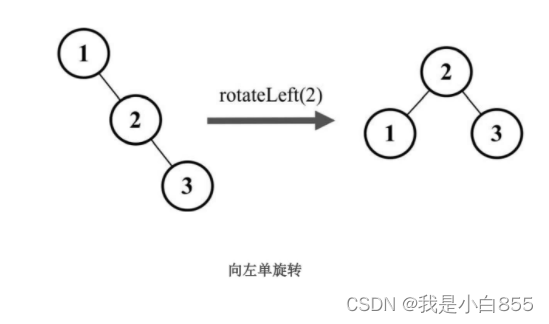
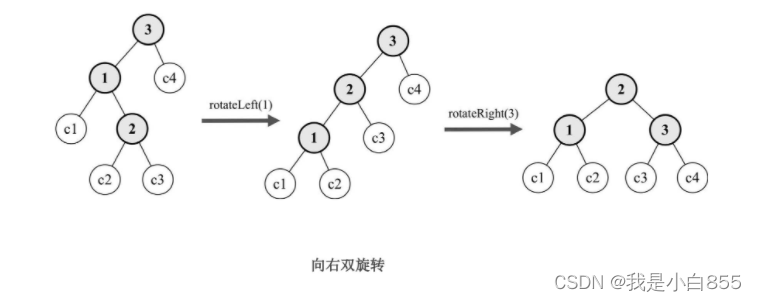
红黑树
AVL树相对于红黑树,它的插入/删除操作效率都不高。
R-B tree
红黑树是一种自平衡的二叉搜索树,以前叫做平衡二叉B树
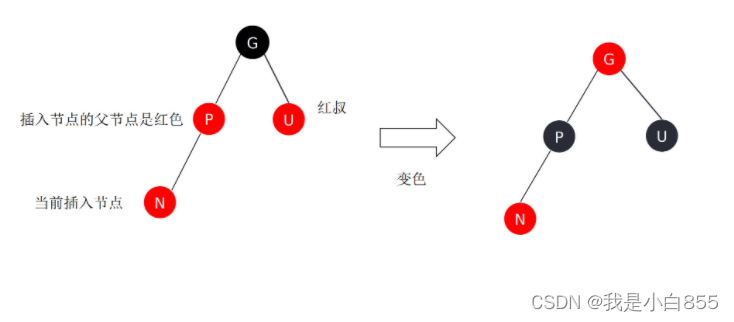
红黑树增加的一些特性
1、结点是红色或者黑色。(结点上有一个color属性)
class Node {
constructor(){
this.color = 'black'
}
}2、根结点是黑色
3、叶子结点都是黑色,且为null (NIL结点)
4、连接红色结点的两个了结点都是黑色,红色结点的父结点都是黑色红色结点的了结点都是黑色
5、从任意结点出发,到其每个叶子结点的路径中包含相同数据的黑色结点
这5条性质就是红黑树给出的自动维持平衡所具备的规则
是为了保证: 从根节点到叶子结点的最长路径不大于最短路径的2倍
红黑树插入数据的时候。会先去遍历数据应该插入到哪个位置,插入的数据一定是红色的。
const RED = 'red';
const BLACK ='black';
class Node {
constructor(index,value){
this.index = index;
this.value = value;
this.color = RED; // 新增加 默认红色
}
}
this.color = BLACK