前言

前一篇文章介绍用数组实现的顺序表时已经提到链表这种结构，在STL中的 list 就是以链表实现的顺序表。这种结构与数组相比最大好处就是可以很方便的在头部和中部插入数据，而数组比较麻烦，需要移动之后的所有数据。

一、链表简介

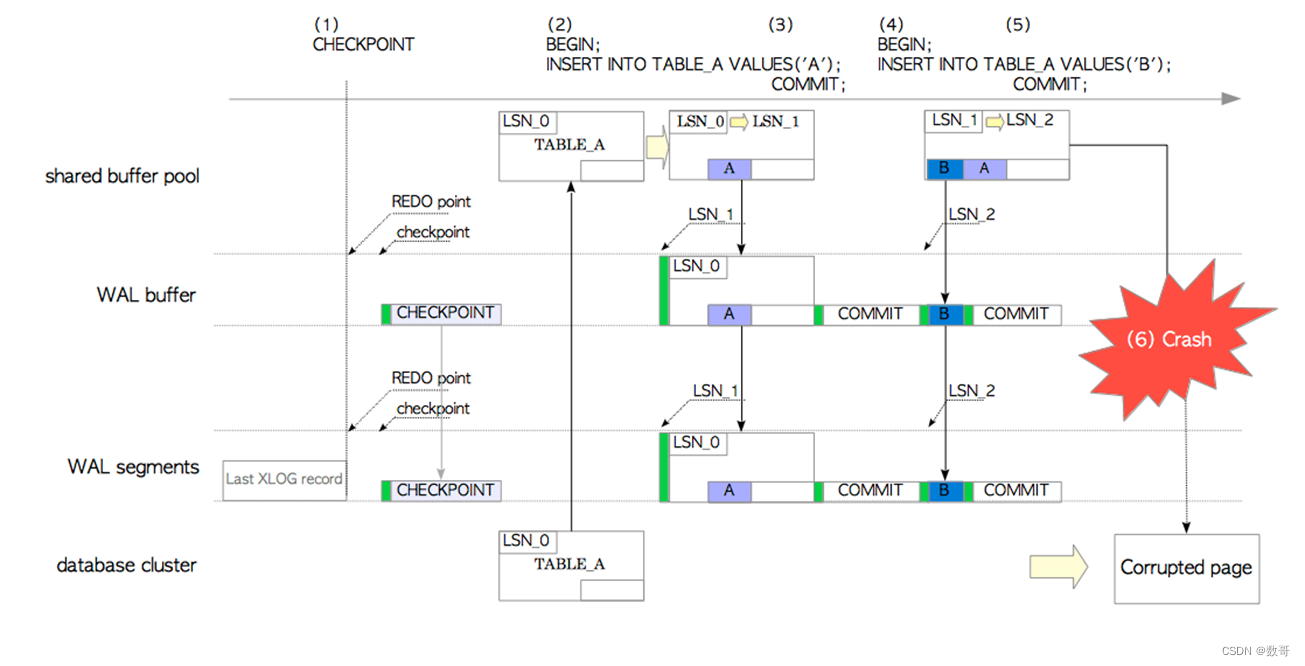
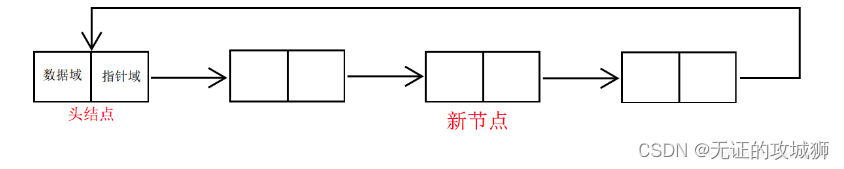
链表也可以实现顺序表的功能。链表是一种动态数据结构，它可以根据需要自动调整大小，存储不连续的元素。当链表每个节点只记录下一个节点的指针时，它只能实现从前往后的单向访问，称之为单链表。如图所示：
在这里插入图片描述
h 表示链表的开头，它只存储了后面的第一个元素的地址，之后的每个节点存储了本身的值和此节点后的一个地址。就像一根链条将所有元素联系起来，大概这也是其称作链表的原因。

很显然的，有单链表了，自然能想到在最后一个节点中存储头或第一个节点的地址。如此就是单向循环链表，如图

再进一步我在每个节点都再存储前一个节点的地址呢，就实现了双向链表：
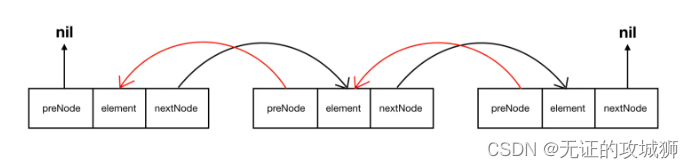
在这里插入图片描述
很显然也是有双向循环链表的：

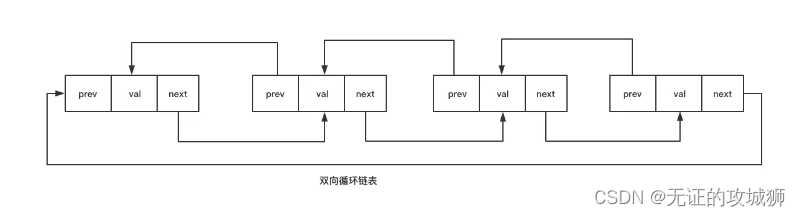
看图就明白了，链表的优点是在中间或开头插入或删除元素时，不需要移动后面的元素，效率较高。缺点是不能快速地随机访问任意元素，需要遍历，而且比较占空间。链表在计算机中的存储方式与普通数组不同，它采用指针来存放元素。下面我们就用代码来实现一个简单的顺序表的例子：

二、单链表实现

#include <iostream>
using namespace std;

template <typename T> class Node {
public:
    T data;
    Node<T>* next;
};

template <typename T> class LinkedList {
private:
    Node<T>* head;
    int len;
public:
    LinkList() {
        head = new Node<T>;
        head->next = NULL; //(*head).next = NULL;
        len = 0;
    }

    ~LinkList() {
        Node<T>* p = head;
        while (p != NULL) {
            Node<T>* q = p->next;
            delete p;
            p = q;
        }
    }

    bool insert(int i, T data) {
        if (i < 0 || i > len) {
            return false;
        }
        Node<T>* p = head;
        for (int j = 0; j < i; j++) {
            p = p->next;
        }
        Node<T>* q = new Node<T>;
        q->data = data;
        q->next = p->next;
        p->next = q;
        len++;
        return true;
    }

    bool remove(int i) {
        if (i < 0 || i >= len) {
            return false;
        }
        Node<T>* p = head;
        for (int j = 0; j < i; j++) {
            p = p->next;
        }
        Node<T>* q = p->next;
        p->next = q->next;
        delete q;
        len--;
        return true;
    }

    int length() const {
        return len;
    }

    bool get(int i, T& data) const {
        if (i < 0 || i >= len) {
            return false;
        }
        Node<T>* p = head->next;
        for (int j = 0; j < i; j++) {
            p = p->next;
        }
        data = p->data;
        return true;
    }
};

在上面代码中，我们定义了一个 Node 类和一个 LinkList 类。其中 Node 类表示链表中的一个节点，包含数据和指向下一个节点的指针；LinkedList 类表示一个链表，包含头节点和链表长度。这个例子中实现了插入、删除、获取长度和获取元素等方法。

head->next 是链表中的一个指针，指向链表的第一个节点。head->next 表示链表的首节点，head 本身并没有值，它只是一个指向首节点的指针。head 的下一个节点才是第一个节点。

二、代码解读

相对于数组实现的顺序表，链表要稍复杂一些。第一个类定义了节点的数据结构，当然用struck也是可以的。next 是一个指针，用于指向下一个地址。

构造函数中 head->next = NULL; //(*head).next = NULL; 使用了指针的写法，这种写法略微方便点，如注释的写法也是可以的。因为 head 是一个指针，用->指针可以直接得到 head 的成员，如果写成类.成员就要先对指针解引，所以要有括号表示运算的优化级。

析构函数直接通过最后的元素的下一个指针是 NULL 这个特征，沿着链表一直删除。

insert方法需要先判断插入的位置是否合法，如果i在范围内，则找到当前的这个第 i 项的前一个元素。所以 for 循环中的条件是 < i ，然后将 i-1 项的 next 指针指向插入元素，将新元素的next 改成原 i-1 项的 next。如此即完成插入方法。下一个方法 remove 其实就是 insert 方法的逆序。

get 方法是用于读取元素值的，T& data 这个形参表示：这里使用了一个引用去取值。会将第 i 项的值存入传入的实参中，这是一个简单的引用写法。

三、链表的优缺点

链表的主要缺点就是查找不方便，每一次取值都将遍历从头到 i ，时间复杂度相较数组在查找知道是第几项的情况下会慢很多，因为数组可以直接以下标取值。
链表在往中间插入数据时会方便很多，数组需要每次移动插入位置后的所有元素。
链表不需要连续大片的内存块，对内存的利用更充分。但是链表因为要存储下一个元素的指针，双向链表更是要存上一个元素的指针。所以同样的数据相对于数组所占用的内存会多得多，在64位系统中每个指针就占了8个字节，而一个 int 整数才占4字节。
链表的另一种结构双向链表可以实现队列的功能。STL中的 list 就有 pop_front、push_back 这两个成员函数，很容易实现 FIFO 先进先出的功能。
单向链表用NULL来判断是否到了尾部，环形链表可以用是否遇到头节点指针判断。
双向链表因为存储了上一个节点的指针，可以实现双向迭代。弥补了相对数组的一个大缺点。