VC GDI双缓冲绘图

双缓冲绘图，知道这个知识点，每次用的时候还得踩一遍坑，真是服，总结记录一下，下次抄~

创建内存DC和内存图片，缺一不可

创建的内存DC需要绘制到内存图片上，绘制完成以后再拷贝到内存DC，所有两者缺一不可。

void CImageView::OnDraw(CDC* pDC)
{
	// TODO: 在此添加专用代码和/或调用基类
	CRect rect;
	GetClientRect(&rect);
	CDC memDC;
	memDC.CreateCompatibleDC(pDC);
	CBitmap bitmap;
	bitmap.CreateCompatibleBitmap(pDC, rect.Width(), rect.Height());
	CBitmap* preBitmap = memDC.SelectObject(&bitmap);

	OnCompatibleDraw(&memDC);

	pDC->BitBlt(0, 0, rect.Width(), rect.Height(), &memDC, 0, 0, SRCCOPY);
	memDC.SelectObject(preBitmap);
	bitmap.DeleteObject();
	memDC.DeleteDC();
}

最好是封装一下内存绘制

void CImageView::OnCompatibleDraw(CDC * pDC)
{
	CMFCCompleteDoc* pDoc = (CMFCCompleteDoc*)GetDocument();
	if (pDoc != nullptr)
	{
		pDoc->m_UnitManager.OnDraw(pDC);
	}
}

绘制效果 关键是不闪烁

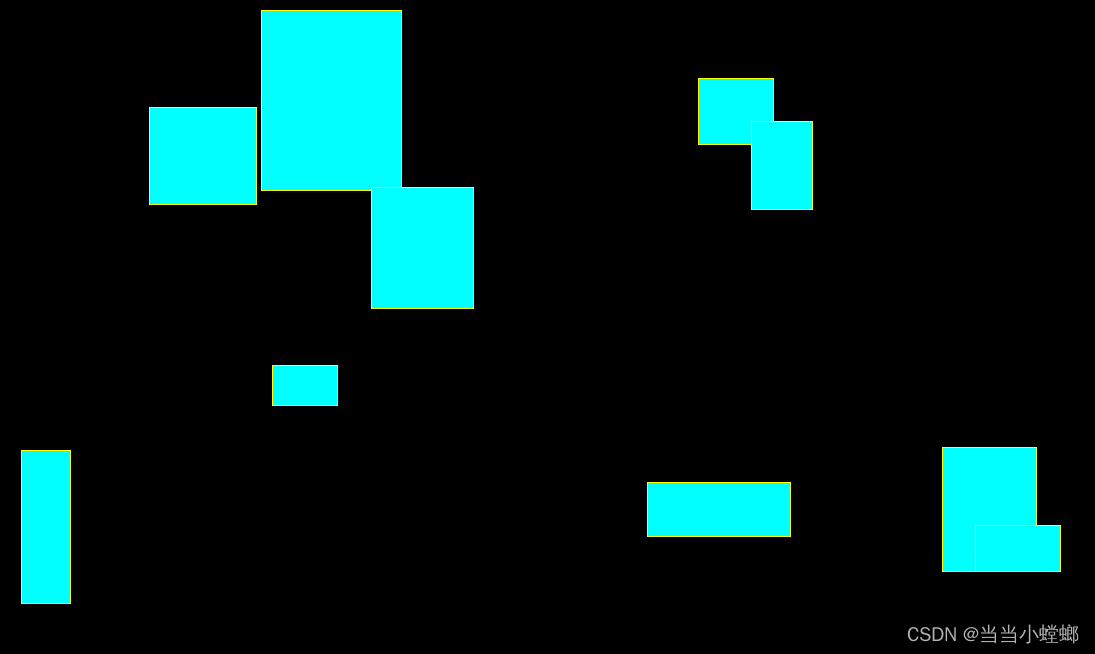
PS 重绘机制

由于是每次新建的内存DC和内存的图片，所以窗口失效可以选择不重新绘制，如果不是重新创建的内存DC和内存图片，则需要手动清空内存DC和内存图片。

问：需要每次重建内存DC和内存图片吗？
答：需要，因为设备DC随时会发生变化，例如窗口大小。如果需要不每次重建提升效率，则设备DC发生变化的所有地方需要重新创建内存DC和内存图片

void CMFCCompleteDoc::OnIdle()
{
	CDocument::OnIdle();

	CView* pView = GetActiveView();
	if (pView == nullptr)
	{
		return;
	}

	if (pView->IsKindOf(RUNTIME_CLASS(CImageView)))
	{
		CRect rect;
		pView->GetClientRect(&rect);
		pView->InvalidateRect(&rect, FALSE);
	}
}