层序遍历（广度优先遍历）：

遍历思路：
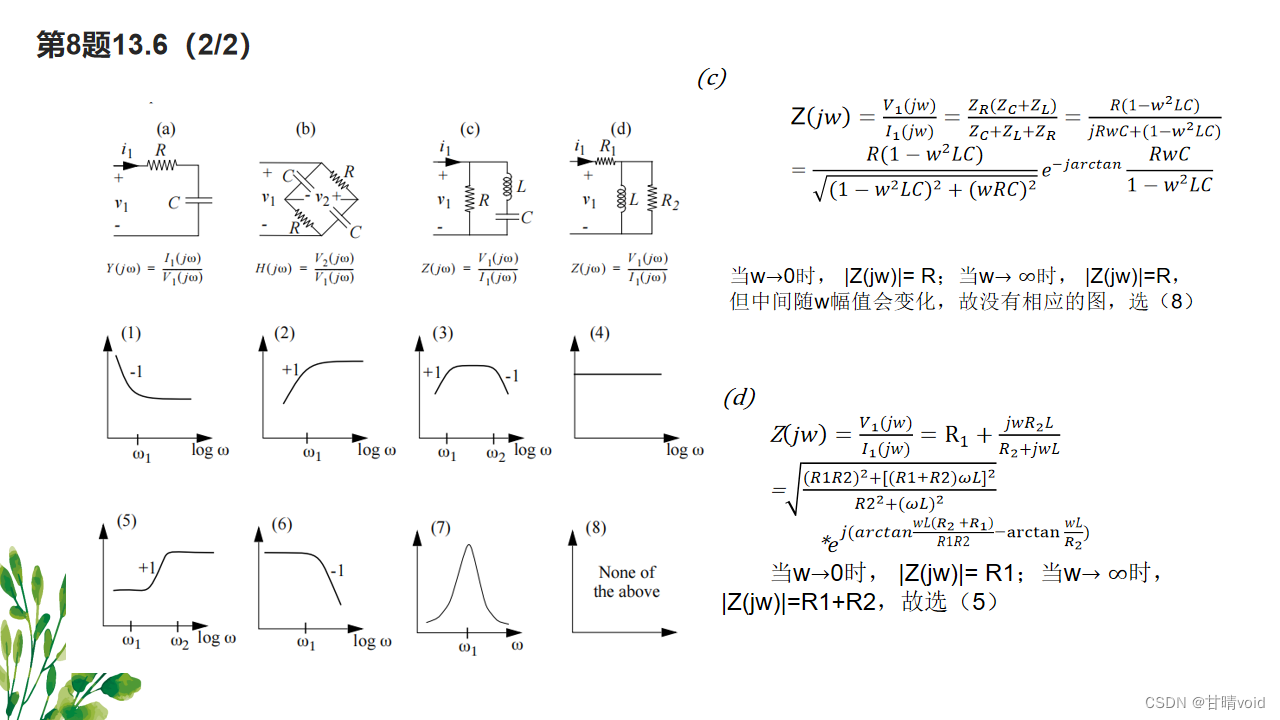
借用队列来实现。
若根节点不为空，则先将根节点放入队列，
随后，在while循环中，判断队列当前的size，队列的size就是树在该层中的节点数量，所以有几个节点就要利用for循环分别将这几个节点的子节点再放入队列

class Solution {
public:
    vector<vector<int>> levelOrder(TreeNode* root) {
        queue<TreeNode*> MyQueue;
        vector<vector<int>> Res;
        vector<int> Temp;
        TreeNode* cur = root;

        if(root == nullptr)
          return Res;

        MyQueue.push(cur);
        
        while(!MyQueue.empty())
        {
            int size = MyQueue.size();
            for(int i=0;i<size;i++)
            {
                cur = MyQueue.front();
                Temp.push_back(cur->val);
                MyQueue.pop();
                
                if(cur->left) MyQueue.push(cur->left);
                if(cur->right) MyQueue.push(cur->right);
            }
            Res.push_back(Temp);
            Temp.clear();            
        }
        return Res;
    }
};

以下十题都可以安装这个思路进行编写：

• 102.二叉树的层序遍历
• 107.二叉树的层次遍历II
• 199.二叉树的右视图
• 637.二叉树的层平均值
• 429.N叉树的层序遍历
• 515.在每个树行中找最大值
• 116.填充每个节点的下一个右侧节点指针
• 117.填充每个节点的下一个右侧节点指针II
• 104.二叉树的最大深度
• 111.二叉树的最小深度

翻转二叉树 

题目链接：力扣

解题思路：这道题最关键的点在于 想清楚用那种遍历方式进行遍历
——前序和后序遍历较方便，用中序遍历会很绕，容易给自己踩坑

递归法

其实还是前序遍历的逻辑，先交换左右子树节点，然后交换左子树，再交换右子树

    TreeNode* invertTree1(TreeNode* root) {

        if(root == nullptr)
        return nullptr;

        TreeNode* Temp = root->left;
        root->left =root->right;
        root->right = Temp;

        invertTree(root->left);
        invertTree(root->right);
        return root;

    }

 迭代法

在前序遍历的基础上加以改动

 TreeNode* invertTree(TreeNode* root)
    {
        queue<TreeNode*> myqueue;
        TreeNode* cur = root;
        if(!cur) return nullptr;

        myqueue.push(cur);

        while(!myqueue.empty())
        {
            cur = myqueue.front();
            myqueue.pop();
            swap(cur->left, cur->right);

            if(cur->right) myqueue.push(cur->right);
            if(cur->left)  myqueue.push(cur->left);
        }

        return root;
    }

对称二叉树

递归法

题目链接：力扣 

解题思路：本质是比较根节点的左子树与右子树是不是相互翻转的，即我们要比较的是两个树（这两个树是根节点的左右子树），所以在递归遍历的过程中，也是要同时遍历两棵树。

 一个树的遍历顺序是左右中，一个树的遍历顺序是右左中。

class Solution {
public:
    bool isSymmetric(TreeNode* root) {

        if(!root)  return true;
        return compare(root->left,root->right);
    }

    bool compare(TreeNode* left, TreeNode* right)
    {
        if(left == nullptr && right != nullptr) return false;
        else if(left != nullptr && right == nullptr) return false;
        else if(left == nullptr && right == nullptr) return true;
        else if(left->val != right->val) return false;
        else return compare(left->left,right->right) && compare(left->right, right->left);
    }

};

迭代法 

逻辑和递归法是一样的，使用队列来比较两个树（根节点的左右子树）是否相互翻转

class Solution {
public:
    bool isSymmetric(TreeNode* root) {
        if (root == NULL) return true;
        queue<TreeNode*> que;
        que.push(root->left);   // 将左子树头结点加入队列
        que.push(root->right);  // 将右子树头结点加入队列
        
        while (!que.empty()) {  // 接下来就要判断这两个树是否相互翻转
            TreeNode* leftNode = que.front(); que.pop();
            TreeNode* rightNode = que.front(); que.pop();
            if (!leftNode && !rightNode) {  // 左节点为空、右节点为空，此时说明是对称的
                continue;
            }

            // 左右一个节点不为空，或者都不为空但数值不相同，返回false
            if ((!leftNode || !rightNode || (leftNode->val != rightNode->val))) {
                return false;
            }
            que.push(leftNode->left);   // 加入左节点左孩子
            que.push(rightNode->right); // 加入右节点右孩子
            que.push(leftNode->right);  // 加入左节点右孩子
            que.push(rightNode->left);  // 加入右节点左孩子
        }
        return true;
    }
};