Powered by:NEFU AB-IN
Link
文章目录
- 2172. 最大公约数
- 题意
- 思路
- 代码
2022年第十三届决赛真题
2172. 最大公约数
-
题意
给定一个数组, 每次操作可以选择数组中任意两个相邻的元素 x , y x, yx,y 并将其 中的一个元素替换为 gcd ( x , y ) \operatorname{gcd}(x, y)gcd(x,y), 其中 gcd ( x , y ) \operatorname{gcd}(x, y)gcd(x,y) 表示 x xx 和 y yy 的最大公约数。 请问最少需要多少次操作才能让整个数组只含 1 。
-
思路
流程图如下
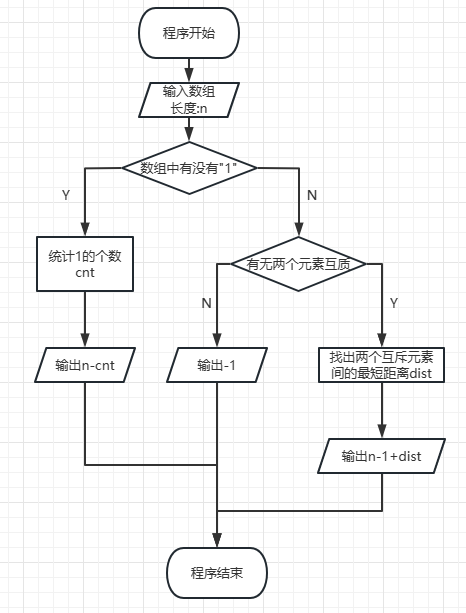
其中两个互质元素的最短距离,可以这么求:- 首先,目的就是为了让数组中变出一个1,而题目中只让相邻gcd,所以两个互质的不能直接gcd
- 所以我们要进行区间gcd,找到最短长度的区间,使得gcd=1
- 如abcde,a与e互质,其实相当于a或e中无一个质因子相同,所以也就是a和b进行gcd,然后b肯定会带上a的因子,否则b就是1,然后一直到e
- 可以采用二分或双指针,找最短长度区间
- 可以采用st表或线段树,求区间gcd
-
代码
''' Author: NEFU AB-IN Date: 2023-05-24 12:47:50 FilePath: \LanQiao\2172\2172.py LastEditTime: 2023-05-24 14:52:22 ''' # import from sys import setrecursionlimit, stdin, stdout, exit from collections import Counter, deque from heapq import heapify, heappop, heappush, nlargest, nsmallest from bisect import bisect_left, bisect_right from datetime import datetime, timedelta from string import ascii_lowercase, ascii_uppercase from math import log, gcd, sqrt, fabs, ceil, floor class sa: def __init__(self, x, y): self.x = x self.y = y def __lt__(self, a): return self.x < a.x # Final N = int(1e5 + 10) M = 20 INF = int(2e9) # Define setrecursionlimit(INF) input = lambda: stdin.readline().rstrip("\r\n") # Remove when Mutiple data read = lambda: map(int, input().split()) LTN = lambda x: ord(x.upper()) - 65 # A -> 0 NTL = lambda x: ascii_uppercase[x] # 0 -> A # —————————————————————Division line —————————————————————— a = [0] * N dp = [[0] * M for _ in range(N)] Log = [0] * N def init(): for j in range(M): i = 1 while i + (1 << j) - 1 <= n: if j == 0: dp[i][j] = a[i] else: dp[i][j] = gcd(dp[i][j - 1], dp[i + (1 << (j - 1))][j - 1]) i += 1 Log[1] = 0 for i in range(2, N): Log[i] = Log[i >> 1] + 1 def query(l, r): k = Log[r - l + 1] return gcd(dp[l][k], dp[r - (1 << k) + 1][k]) n, = read() a[1:] = read() init() cnt = sum(i == 1 for i in a) if cnt > 0: print(n - cnt) exit(0) if query(1, n) != 1: print(-1) exit(0) ans = INF for i in range(1, n + 1): l, r = i, n while l < r: mid = (l + r) >> 1 if query(i, mid) == 1: r = mid else: l = mid + 1 if query(i, r) == 1: ans = min(ans, r - i) print(ans + n - 1)