前言:基本是为了我自己看的一些我容易忘记的东西,为考试作准备把,主要使后半部分的知识,前半部分请看算法设计与分析阶段考总结
第五章
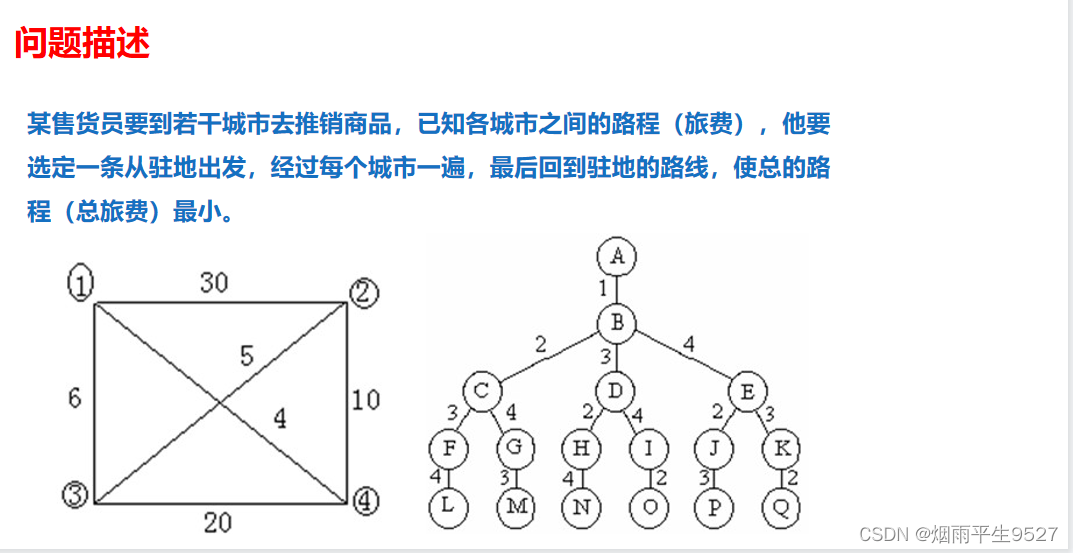
回溯算法是一种系统地搜索问题的解的方法。某个问题的所有可能解的称为问题的解空间,若解空间是有限的,则可将解空间映射成树形结构。回溯算法的基本思想是:从一条路往前走,能进则进,不能进则退回来,换一条路再试。
相关概念1
- 扩展结点
- 活结点
- 死结点
相关概念2
- 子集树:遍历子集树需O(2n)计算时间
- 排列树:遍历排列树需O(n!)计算时间
第六章
分支限界法是一种求解最优化问题的算法,常以广度优先或以最小耗费(最大效益)优先的方式搜索问题的解空间树。其基本思想是把问题的可行解展开,再由各个分支寻找最佳解。
在分支限界法中,分支是使用广度优先策略,依次生成扩展结点的所有分支。限界是在结点扩展过程中,计算结点的上界,搜索的同时剪掉某些分支。
与回溯法区别求解目标不同
- 回溯法是找出满足约束条件的所有解
- 分支限界法是找出满足条件的一个解,或某种意义下的最优解
搜索方式不同
- 回溯法:深度优先
- 分支限界法:广度优先或最小耗费优先
相关概念
- 活结点
- 活结点表PT
- 扩展结点
- 儿子结点
- 队列式分支限界法
- 优先队列式分支限界法
第七章
随机化算法大致分为四类:
- 数值随机化算法
- 蒙特卡罗算法
- 拉斯维加斯算法
- 舍伍德算法
随机化算法的输入
- 原问题的输入
- 随机选择的随机数序列
数值化随机算法常用于数值问题求解。这类算法得到的往往是近似解,且近似解的精度随着计算时间的增加而不断提高。在许多情况下,要计算出问题的精确解是不可能的或没有必要的,用数值化税基算法可得到相当满意的解。
数值类问题常用多见于 各种积分微分,数学计算中。
蒙特卡罗算法用于求问题的准确解。对许多问题,近似解是毫无意义的。用蒙特卡罗算法能求得问题的一个解,但这个解未必是正确的。其求得正确解的概率依赖算法所用的时间。算法所用时间越多,得到正确解的概率就越高。蒙特卡罗算法的主要缺点也在于此。一般情况下,无法有效的判断所得到的解是否可定正确。(非一般情况是可以判定的!)
拉斯维加斯算法不会得到不正确的解。一旦用拉斯维加斯算法找到一个解,这个解就一定是正确解。但有时用拉斯维加斯算法会找不到解。拉斯维加斯算法找到正确解的概率会随着它所用的计算时间的增加而提高。
舍伍德算法 总能求得问题的一个正确解,消除算法最坏情形行为与特定实例之间的关联性,并不提高平均性能,也不是刻意避免算法的最坏情况行为
注意事项
- 随机化算法的结果不能保证一定是正确的,但可以限定其出错概率;
- 随机化算法在不同的运行中,对于相同的输入实例可以有不同的结果,因此,对于相同的输入实例,随机化算法的执行时间可能不同。
算法分析
回溯法
批处理作业调度(猜)
给定n个作业的集合{J1,J2,…,Jn}。每个作业必须先由机器1处理,然后由机器2处理。作业Ji需要机器j的处理时间为tij。对于一个确定的作业调度,设Fij是作业i在机器j上完成处理的时间。所有作业在机器2上完成处理的时间和称为该作业调度的完成时间和。 批处理作业调度问题要求对于给定的n个作业,制定最佳作业调度方案,使其完成时间和达到最小。
N后问题(略)
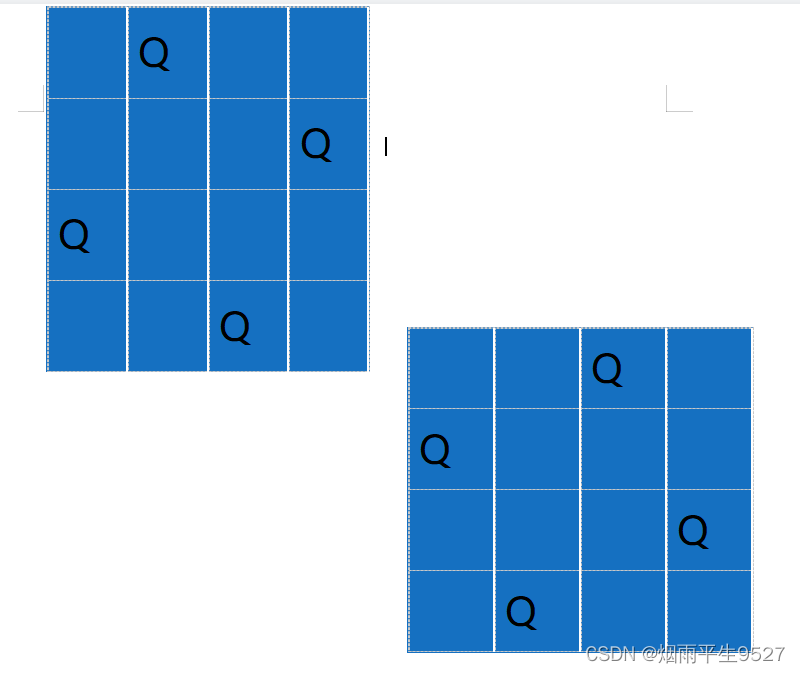
在n×n格的棋盘上放置彼此不受攻击的n个皇后。按照国际象棋的规则,皇后可以攻击与之处在同一行或同一列或同一斜线上的棋子。n后问题等价于在n×n格的棋盘上放置n个皇后,任何2个皇后不放在同一行或同一列或同一斜线上。 当且仅当 n = 1 或 n ≥ 4 时问题有解。
思路
四后问题解法
符号三角形问题(略)
思路
用n元组x[1:n]表示符号三角形的第一行的n个符号,当x[i]等于1时,表示符号三角形的第一行的第i个符号为“+”;当x[i]等于0时,表示符号三角形的第一行的第i个符号为“-”;1<=i<=n。由于x[i]是2值的。所以在用回溯法解符号三角形问题时,可以用一棵完全二叉树来表示其解空间。在符号三角形的第一行的前i个符号x[1:i]确定后,就确定了一个有i*(i+1)/2个符号组成的符号三角形。
(i*(i+1)/2来自首项为1、公差为1的等差数列的求和公式)
无解的判断: n*(n+1)/2为奇数
0-1背包问题
习题:0-1背包问题的一个实例为:n=4,c=16,p=[22,21,16,7],w=[11,10,8,7]。依据回溯法求解该问题,试回答如下问题:
(1)该问题的约束函数是什么?
(2)请画出求得最优解的解空间树。要求中间被舍弃的结点(不满足约束条件的解)用×标记,获得中间解的结点用单圆圈○框起,最优解用双圆圈◎框起。
答:(1)约束函数为: ∑wixi≤C,即背包能装下物品
(2)解空间树如下图所示。
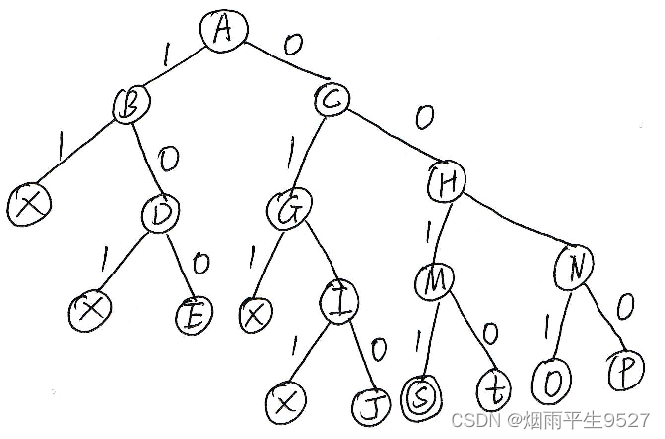
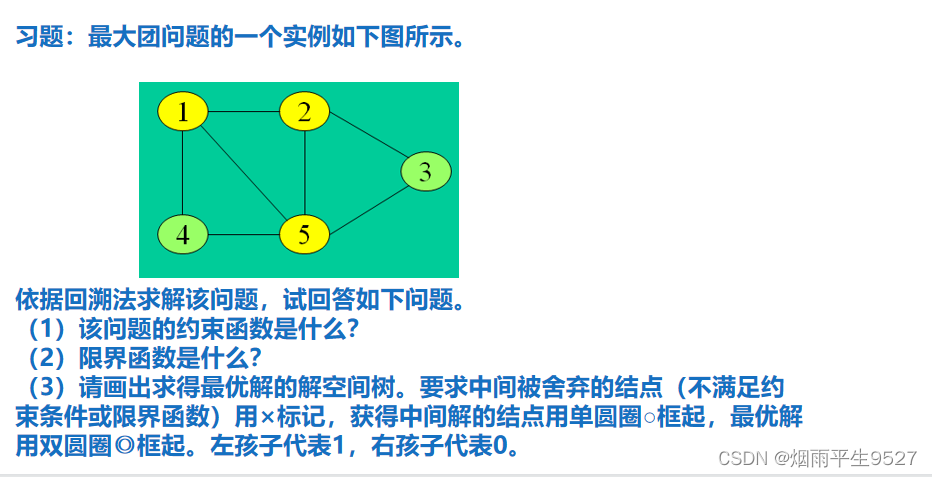
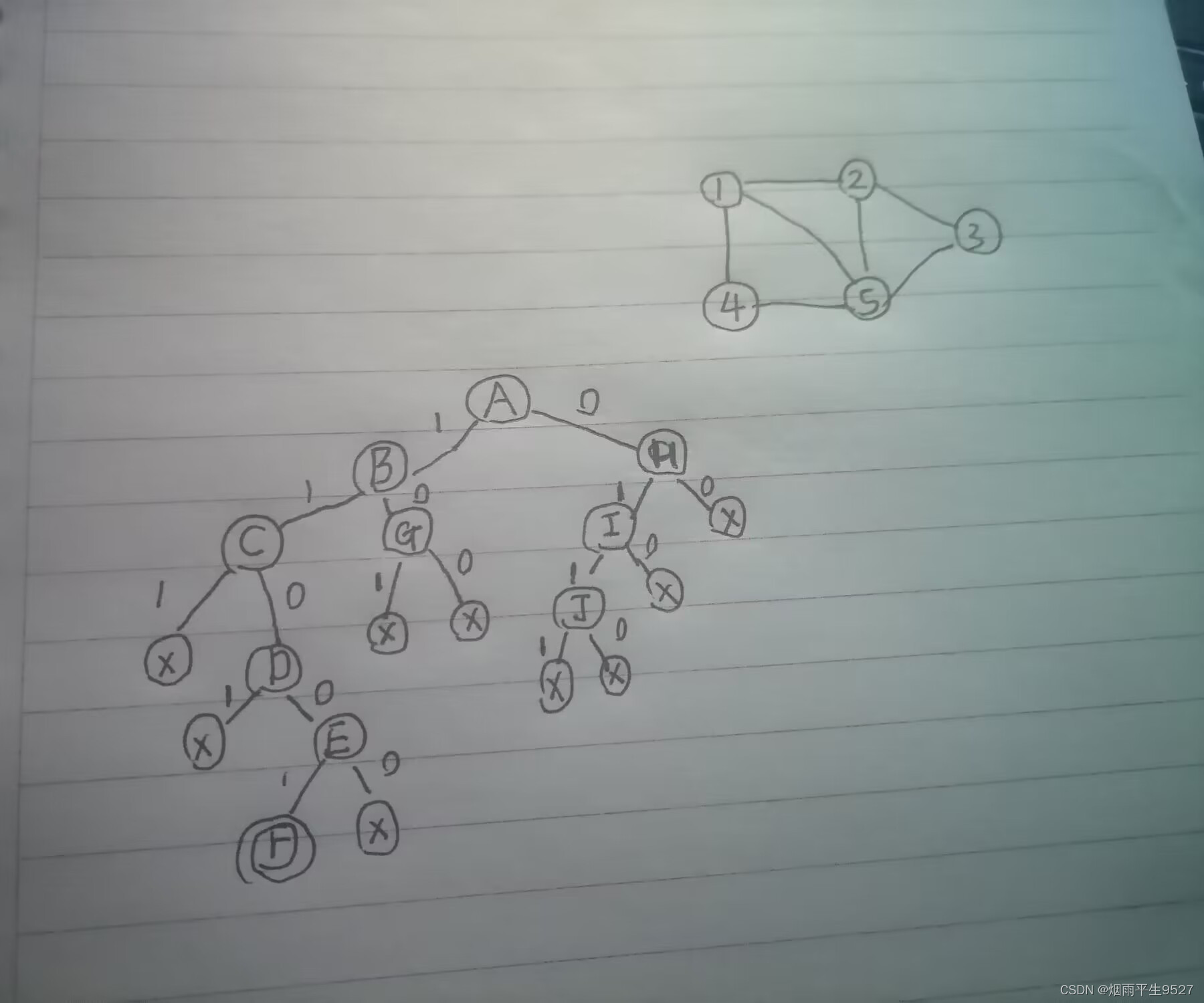
最大团习题 (猜)
可行性约束函数:当前顶点到已选入的顶点集中每一个顶点都有边相连。
(2)限界函数:有足够多的可选择顶点使得算法有可能在右子树中找到更大的团。
分支限界
0-1背包问题
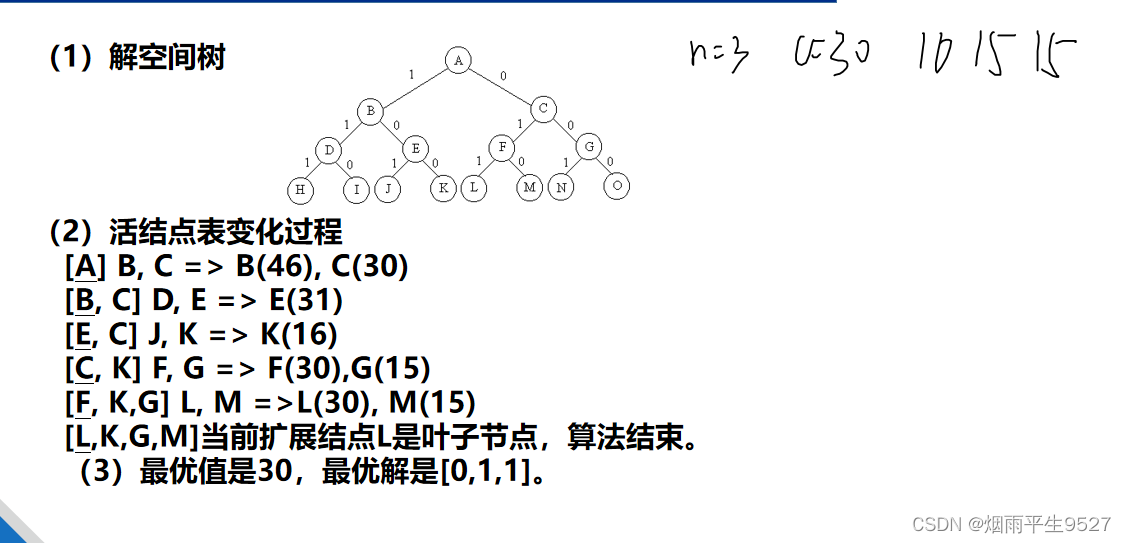
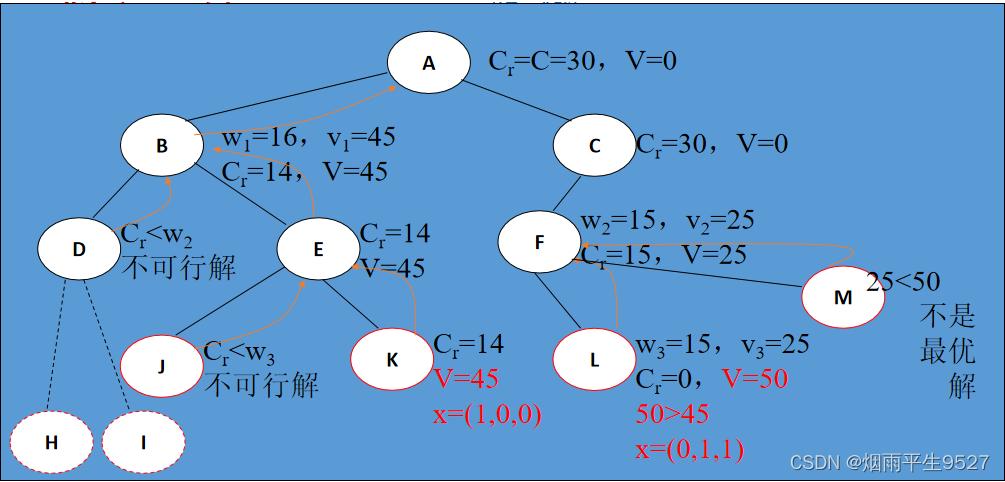
考虑如下0-1背包问题的实例: n=3, c=30, w=[16,15,15], v=[45,25,25]
分支限界
旅行售货员问题 (同样的思路只放PPT了)(略)
队列式分支限界法
优先队列式分支限界法
装载问题同理
队列式分支限界法
优先队列式分支限界法(猜)
给出优先队列式分支限界法解该实例时,活结点表的变化过程(优先级为当前轮船中集装箱重量加上剩余集装箱重量之和)。描述方式:[A,B,C]FGF(40),其中[A,B,C]是活结点表,A是当前扩展结点,由A生成FG,其中G不满足约束条件被裁剪掉,40表示结点F的优先级
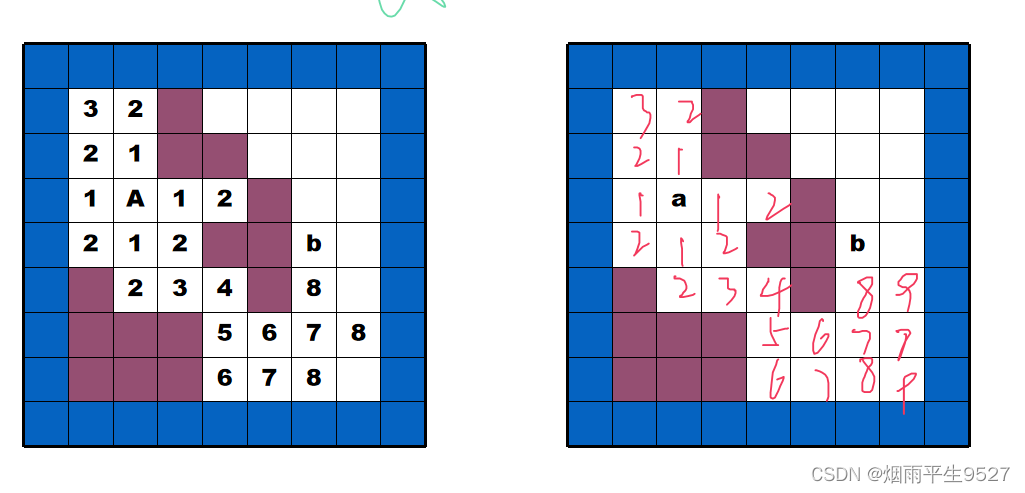
布线问题实例
随机化算法
随机数
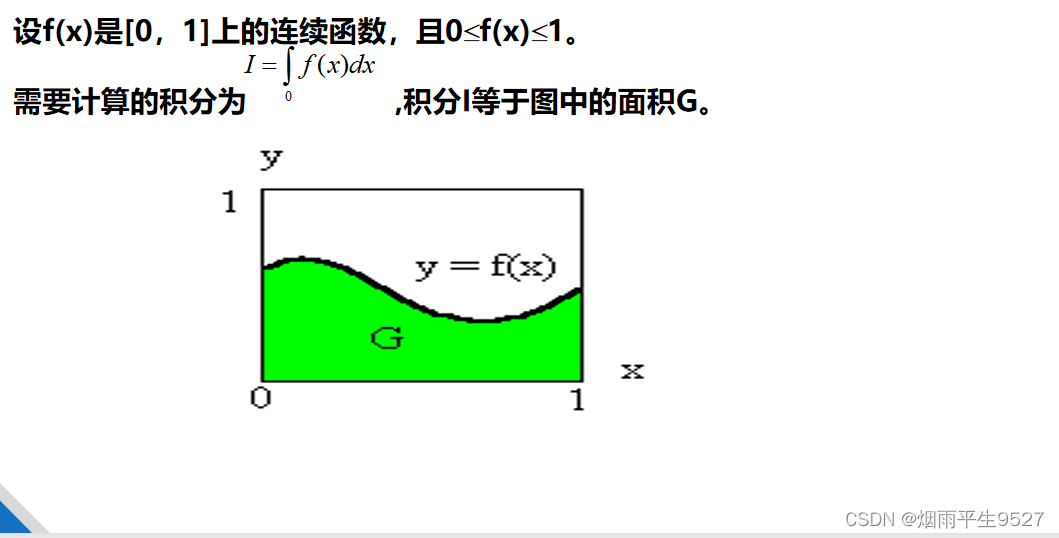
随机投点法计算定积分
蒙特卡罗(MonteCarlo)型随机化算法
程序设计
回溯法
装载问题
问题描述
有一批共n个集装箱要装上2艘载重量分别为C1和C2的轮船,其中集装箱i的重量为wi,且∑wi≤C1+C2 装载问题要求确定是否有一个合理的装载方案可将这个集装箱装上这2艘轮船。如果有,找出一种装载方案。 容易证明,如果一个给定装载问题有解,则采用下面的策略可得到最优装载方案: (1)首先将第一艘轮船尽可能装满; (2)将剩余的集装箱装上第二艘轮船。
问题分析
关键代码
// 搜索到叶子节点 if (i > n) { // 如果找到更优解,则更新最优解 if (cw > bestw) { bestw = cw; for (int j = 1; j <= n; j++) { best[j] = x[j]; } } return; } // 搜索左子树 r -= w[i]; if (cw + w[i] <= c) { x[i] = 1; cw += w[i]; backtrack(i + 1); cw -= w[i]; } r += w[i]; // 搜索右子树 if (cw + r > bestw) { x[i] = 0; backtrack(i + 1); }详细代码
#include <stdio.h> #define MAX_N 20 int n; // 货物数量 int c; // 车的载重量 int w[MAX_N],x[MAX_N]; // 每个货物的重量 int best[MAX_N]; // 最优解 int cw; // 当前载重量 int bestw; // 最优载重量 int r; // 剩余物品重量和 // 搜索装载方案 void backtrack(int i) { // 搜索到叶子节点 if (i > n) { // 如果找到更优解,则更新最优解 if (cw > bestw) { bestw = cw; for (int j = 1; j <= n; j++) { best[j] = x[j]; } } return; } // 搜索左子树 r -= w[i]; if (cw + w[i] <= c) { x[i] = 1; cw += w[i]; backtrack(i + 1); cw -= w[i]; } r += w[i]; // 搜索右子树 if (cw + r > bestw) { x[i] = 0; backtrack(i + 1); } } int main() { //printf("请输入货物数量和车的载重量(用空格分隔):\n"); scanf("%d%d", &n, &c); //printf("请输入每个货物的重量:\n"); for (int i = 1; i <= n; i++) { scanf("%d", &w[i]); r += w[i]; } backtrack(1); printf("最优装载方案为:\n"); for (int i = 1; i <= n; i++) { if (best[i]) { printf("%d ", i); } } printf("\n最优载重量为:%d\n", bestw); return 0; }
0-1背包(PPT写的又丑又水,考试推荐·下述代码)
PPT·代码请参考博客回溯算法设计实验
其中关键代码为
int bound(int t) { int cleft = C - CurWeight;//剩余容量 int b = CurValue;//现阶段背包内物品的价值 while (t <= n && w[t] <= cleft)//以物品重量价值递减装入物品 { cleft = cleft - w[t]; b = b + v[t]; t++; } if (t <= n)//装满背包 b = b + v[t] * cleft / w[t];//计算t号物品的单位价值装满剩余空间 return b; } void backtrack(int t) { if (t > n)//到达叶子节点了 { if (CurValue > BestValue)//已经搜寻完一次了,把现有的最大值赋值; { BestValue = CurValue; for (int i = 1; i <= n; i++) BestX[i] = X[i]; } return; } if (CurWeight + w[t] <= C)//不到背包最大容量进入左子树 { X[t] = 1;//记录是否装入 CurWeight += w[t]; CurValue += v[t]; backtrack(t + 1);//回溯 CurWeight -= w[t]; CurValue -= v[t]; } if (bound(t + 1) > BestValue)//进入右子树 { X[t] = 0;//他自己没有后面物品合适 backtrack(t + 1);//判断 } }
问题描述有n个物品,它们有各自的体积和价值,现有给定容量的背包,如何让背包里装入的物品具有最大的价值总和?
注:与普通背包问题不同,0-1背包问题中,物品以整体的形式出现,只能选择整体放入背包或整体不放入背包。
#include <stdio.h> #include <stdlib.h> #define N 100 int n, c, maxValue = 0; // 物品数量,背包容量,最大价值 int w[N], v[N]; // 物品重量,物品价值 int path[N]; int path0[N]; void backtrack(int i, int res, int value) { if (i == n) { if (value > maxValue) { maxValue = value; for (int i = 0; i < n; i++) path0[i] = path[i]; } return; } path[i] = 1; if (res >= w[i]) { backtrack(i + 1, res - w[i], value + v[i]); // 考虑第i个物品放入背包 } path[i] = 0; backtrack(i + 1, res, value); // 不考虑第i个物品放入背包 } int main() { scanf("%d%d", &n, &c); for (int i = 0; i < n; i++) scanf("%d%d", &w[i], &v[i]); backtrack(0, c, 0); printf("%d\n", maxValue); for (int i = 0; i < n; i++) printf("%d ", path0[i]); return 0; }
旅行售货员问题(略)
问题分析
详细代码
#include <stdio.h> #include <stdbool.h> #define MAXN 100 // 最大城市数 int n; // 城市数 int graph[MAXN][MAXN]; // 图的邻接矩阵 int path[MAXN],bestPath[MAXN]; // 保存当前路径 bool visited[MAXN]; // 标记城市是否访问过 int minDist = 0x7fffffff; // 保存最短路径的长度 void backtracking(int cur, int dist) { if (cur == n) { // 所有城市都已经走过了 if (dist + graph[path[n - 1]][0] < minDist) { minDist = dist + graph[path[n - 1]][0]; // 更新最短路径 for(int i = 0;i < n;i++){ bestPath[i] = path[i]; } } return; } for (int i = 1; i < n; i++) { // 枚举下一个城市 if (!visited[i]) { // 如果这个城市还没有访问过 path[cur] = i; // 选择这个城市 visited[i] = true; // 标记这个城市已经访问过 backtracking(cur + 1, dist + graph[path[cur - 1]][i]); // 递归到下一层 visited[i] = false; // 回溯,撤销选择 } } } int main() { scanf("%d", &n); // 输入城市数 for (int i = 0; i < n; i++) { for (int j = 0; j < n; j++) { scanf("%d", &graph[i][j]); // 输入邻接矩阵 } } path[0] = 0; // 起点是城市0 visited[0] = true; // 标记起点已经访问过 backtracking(1, 0); // 从第2个城市开始递归 printf("%d\n", minDist); // 输出最短路径长度 for(int i = 0;i < n;i++){ printf("%d ",bestPath[i]+1); } return 0; }
分支限界法
装载问题
// 定义MaxLoading子函数,用来求解装载问题 // 输入参数:w是一个整型数组,表示集装箱的重量;c是一个整型变量,表示船舶的载重量;n是一个整型变量,表示集装箱的数量;bestx是一个整型数组,用来存储最优解方案 // 返回值:bestw是一个整型变量,表示最优解值 int MaxLoading(int* w, int c, int n, int* bestx) { // 初始化变量 int i = 1; // 当前扩展节点所在层次 int j; // 循环计数器 int bestw = 0; // 最优解值 Heap h; // 优先队列 h.length = 0; // 优先队列的长度初始化为0 int* r = new int[n + 1]; // 剩余集装箱重量之和 r[n] = 0; for (j = n - 1; j > 0; j--) r[j] = r[j + 1] + w[j + 1]; Node* p = new Node; // 当前扩展节点 p->weight = 0; p->level = i; p->parent = NULL; Node* q; // 新生成节点 while (i != n + 1) { // 当还未到达叶子节点时循环 if (p->weight + w[i] <= c) { // 进入左子树,即选择第i个集装箱 q = new Node; // 创建新节点 q->LChild = 1; // 标记为左子树 q->level = p->level + 1; // 层次加一 q->parent = p; // 父节点指向当前扩展节点 q->weight = p->weight + w[i]; // 节点重量等于父节点重量加上第i个集装箱重量 q->uweight = q->weight + r[i]; // 节点上界等于节点重量加上剩余集装箱重量之和 if (q->level == n + 1 && q->weight > bestw) { // 找到更好解 bestw = q->weight; // 更新最优解值 for (j = n; j > 0; j--) { // 更新最优解方案 bestx[j] = q->LChild; q = q->parent; } } else { // 将新生成节点插入优先队列 HeapInsert(h, q); } } if (p->weight + r[i] > bestw) { // 进入右子树,即不选择第i个集装箱,并且满足剪枝条件 q = new Node; // 创建新节点 q->LChild = 0; // 标记为右子树 q->level = p->level + 1; // 层次加一 q->parent = p; // 父节点指向当前扩展节点 q->weight = p->weight; // 节点重量等于父节点重量 q->uweight = q->weight + r[i]; // 节点上界等于节点重量加上剩余集装箱重量之和 if (q->level == n + 1 && q->weight > bestw) { // 找到更好解 bestw = q->weight; // 更新最优解值 for (j = n; j > 0; j--) { // 更新最优解方案 bestx[j] = q->LChild; q = q->parent; } } else { // 将新生成节点插入优先队列 HeapInsert(h, q); } } delete p; // 删除当前扩展节点 if (!h.empty()) { // 取堆顶元素作为下一个扩展节点,并且堆不为空时继续循环 HeapDelete(h, p); i = p->level; } else { // 堆为空则结束循环 break; } } delete[] r; // 删除动态数组r return bestw; // 返回最优解值 }
随机化算
随机快速排序:随机选择枢点的快速排序算法
核心代码
void quickSort(int r[], int low, int high) { srand(time(0)); int i, k; if (low<high) { i=randomNum(low, high); //在区间[low,high]中随机选取一个元素,下标为i r[low]←→r[i]; //交换r[low]和r[i]的值 k=partition(r, low, high); //进行一次划分,得到轴值的位置k quickSort(r, low, k-1);//在前半部分继续查找 quickSort(r, k+1, high);//在后半部分继续查找 } }完整代码
#include <stdio.h> #include <stdlib.h> #include <time.h> //舍伍德(Sherwood)型随机化算法 随机快速排序:随机选择枢点的快速排序算法 //在区间[low,high]中随机选取一个元素,下标为i int randomNum(int low, int high){ return low + rand() % (high - low + 1); } //交换两个元素的值 void swap(int *a, int *b){ int temp = *a; *a = *b; *b = temp; } //进行一次划分,得到轴值的位置k int partition(int r[], int low, int high){ int pivot = r[low]; //选取第一个元素作为轴值 while(low < high){ //循环直到low和high相遇 while(low < high && r[high] >= pivot) high--; //从右向左找到第一个小于轴值的元素 swap(&r[low], &r[high]); //交换r[low]和r[high]的值 while(low < high && r[low] <= pivot) low++; //从左向右找到第一个大于轴值的元素 swap(&r[low], &r[high]); //交换r[low]和r[high]的值 } return low; //返回轴值的位置 } //快速排序函数 void quickSort(int r[], int low, int high) { srand(time(0)); int i, k; if (low<high) { i=randomNum(low, high); //在区间[low,high]中随机选取一个元素,下标为i swap(&r[low], &r[i]); //交换r[low]和r[i]的值 k=partition(r, low, high); //进行一次划分,得到轴值的位置k quickSort(r, low, k-1);//在前半部分继续查找 quickSort(r, k+1, high);//在后半部分继续查找 } } //打印数组 void printArray(int arr[], int n){ int i; for(i=0; i<n; i++){ printf("%d ", arr[i]); } printf("\n"); } //主函数 int main(){ //定义一个数组,表示10个待排序的数 int arr[10] = {23, 45, 12, 67, 89, 34, 56, 78, 90, 11}; //打印原始数组 printf("原始数组:\n"); printArray(arr, 10); //调用快速排序函数 quickSort(arr, 0, 9); //打印排序后的数组 printf("排序后的数组:\n"); printArray(arr, 10); return 0; }八皇后问题(ppt没代码,感觉考的机率不大)
(1)将数组x[8]初始化为0;试探次数count初始化为0;
(2)for (i=1; i<=8; i++)
2.1产生一个[1,8]的随机数j;
2.2 count=count+1,进行第count次试探;
2.3若皇后i(固定在第i行)放置在第j列不发生冲突, 则x[i]=j;count=0; 转步骤(2)(for循环继续运行)放置下一个皇后;
2.4若(count==8),则无法放置皇后i,算法运行失败,
转步骤2.1重新放置皇后i;
(3) 将元素x[1]~x[8]作为八皇后问题的一个解输出。
#include <iostream> #include <cstdlib> #include <ctime> using namespace std; bool isSafe(int x[], int row, int col) { // 检查当前位置是否与之前放置的皇后冲突 for (int i = 1; i < row; i++) { if (x[i] == col || abs(i - row) == abs(x[i] - col)) { return false; } } return true; } void solveEightQueens(int x[], int row) { if (row > 8) { // 所有皇后都放置完成,打印解 for (int i = 1; i <= 8; i++) { cout << x[i] << " "; } cout << endl; } else { for (int j = 1; j <= 8; j++) { if (isSafe(x, row, j)) { x[row] = j; solveEightQueens(x, row + 1); } } } } int main() { srand(time(0)); int x[9] = {0}; // 数组从下标 1 开始使用,初始化为0 solveEightQueens(x, 1); return 0; }代码的输出含义如下:
- 每一行代表一个解,即一个满足条件的皇后摆放方案。
- 每一行有八个数字,分别表示第一行到第八行的皇后所在的列号。
- 例如,第一行输出为4 2 7 3 6 8 5 1,表示第一行的皇后在第四列,第二行的皇后在第二列,依次类推。
- 总共有92种可能的解,即92种不同的皇后摆放方案。
主元素问题
核心代码
bool isMajority(int arr[], int n, int x) { int count = 0; // 记录x出现的次数 for (int i = 0; i < n; i++) { if (arr[i] == x) count++; } return count > n / 2; // 如果x出现次数超过一半,返回true }优化
完整代码
#include <iostream> #include <cstdlib> #include <ctime> using namespace std; // 在区间[low,high]中随机选取一个整数 int randomNum(int low, int high) { return low + rand() % (high - low + 1); } // 判断一个元素是否是主元素,即出现次数超过一半 bool isMajority(int arr[], int n, int x) { int count = 0; // 记录x出现的次数 for (int i = 0; i < n; i++) { if (arr[i] == x) count++; } return count > n / 2; // 如果x出现次数超过一半,返回true } // 蒙特卡罗函数,返回数组中的一个主元素,如果不存在,返回-1 int monteCarlo(int arr[], int n) { srand(time(0)); // 设置随机数种子 int k = 10; // 设置最大尝试次数 // 候选主元素初始化为数组的第一个元素 int candidate = arr[0]; int count = 1; // 记录候选主元素的计数 for (int i = 1; i < n; i++) { if (arr[i] == candidate) { count++; } else { count--; if (count == 0) { // 当前候选主元素计数为0,更新候选主元素为当前元素 candidate = arr[i]; count = 1; } } } // 最后确定的候选主元素需要再次验证 if (isMajority(arr, n, candidate)) { return candidate; // 如果是,返回该元素 } return -1; // 如果不存在主元素,返回-1 } // 打印数组 void printArray(int arr[], int n) { for (int i = 0; i < n; i++) { cout << arr[i] << " "; } cout << endl; } // 主函数 int main() { // 定义一个数组,表示n个待查找的数 int arr[10] = {3, 3, 4, 4, 2, 4, 2, 4, 4,4}; // 打印原始数组 cout << "原始数组:\n"; printArray(arr, 10); // 调用蒙特卡罗函数,返回数组中的一个主元素 int result = monteCarlo(arr, 10); // 打印结果 if (result == -1) { cout << "不存在主元素" << endl; } else { cout << "一个主元素是:" << result << endl; } return 0; }