窗口函数

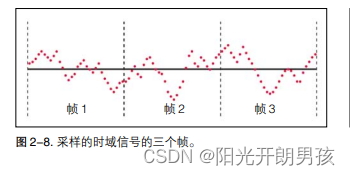
在离散傅立叶变换(DFT)分析运算中，一个固有的假设是要处理的数据是单个周期定期重复的信号。例如，在图2-8中的帧2上应用DFT处理时，信号上会进行周期性扩展。

在连续的帧之间一般会发生不连续点，如图 2-9 所示。

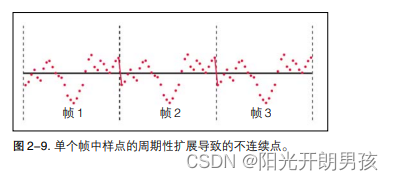
这些人为的不连续点生成原始信号中不存在的杂散响应，这种效应会导致不准确地表示信号，称为频谱泄漏。频谱泄漏不仅会在输出中生成输入中不存在的信号，在附近存在大信号时，还会降低观察小信号的能力。

泰克实时频谱分析仪应用窗口技术，降低频谱泄漏的影响。在执行DFT前，DFT帧乘以窗口函数，样点间的长度相同。窗口函数通常呈钟形，减少或消除了DFT帧尾的不连续点。

窗口函数的选择取决于频响特点，如旁瓣电平、等效噪声带宽和幅度误差。窗口形状还决定着有效 RBW 滤波器。

与其它频谱分析仪一样，RSA 允许用户选择 RBW 滤波器。RSA还允许用户选择多种常用的窗口类型。直接指定窗口形状提高了灵活性，允许用户优化特定测量。例如，应特别注意脉冲信号的频谱分析。如果脉冲周期比窗口长度短，那么应使用均匀的窗口(没有窗口函数)，避免在DFT帧两端产生去加重效应。

窗口函数的频响幅度决定着 R B W 形状。例如，RSA6000 上的 RWB 定义为 3 dB 带宽，与 DFT 中采样频率和样点数量的关系如下：

其中k是与窗口有关的系数，N是DFT计算中使用的时域样点数量，Fs 是采样频率。对 beta1=16.7 的 Kaiser窗口，k约为2.23。RBW形状系数定义为60 dB和3 dB的频谱幅度之间的频率比，约为 4:1。在 RSA6000 上，频谱分析测量使用公式2，根据输入频宽和RBW设置，计算 DFT 要求的样点数量。

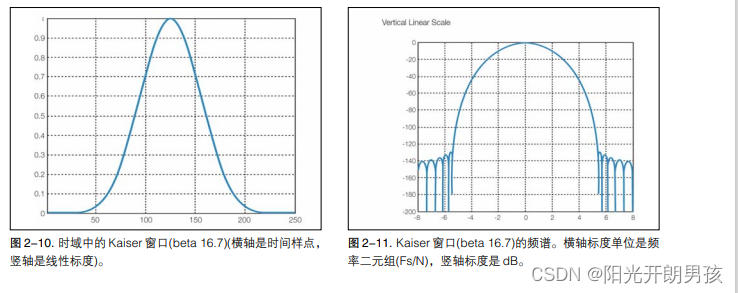
图2-10和图2-11显示了RSA6000分析使用的Kaiser窗口的时域和频谱。这是 RSA6000 在频谱分析中使用的默认窗口。用户可以选择其它窗口(如BlackmanHarris, Uniform, Hanning)，满足专门的测量要求，在执行仪器中提供的部分测量时，也可以使用其它窗口。

实时频谱分析仪中的离散傅立叶变换(DFT)

DFT 定义如下：

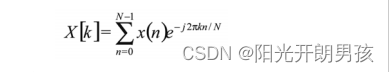
这是实时频谱分析仪的基础，用来从输入序列x(n)中估算各个频率成分 x(k)。DFT基于模块，N是每个DFT模块(或帧)的样点数。输入序列 x(n)是输入信号 x(t)的采样版本。尽管只为n的整数值定义输入序列，但输出是k的连续函数，其中k=(NΩ)/(2Π)，Ω是弧度频率。X[k]的幅度表示x(n)输入序列中存在的频率Ω上频率成分的幅度。

有许多高效的 DFT 计算方法，如快速傅立叶变换(FFT)和 Chirp-Z 变换(CZT)。实现方法的选择取决于应用的特定需求。例如，CZT在选择频率范围和输出点数方面要比FFT灵活。FFT的灵活性较差，但要求的计算较少。RSA 中同时使用 CZT 和 FFT。

解析频率成分的能力不仅依赖于特定的DFT实现方案，还取决于输入序列的时间长度或 RBW。

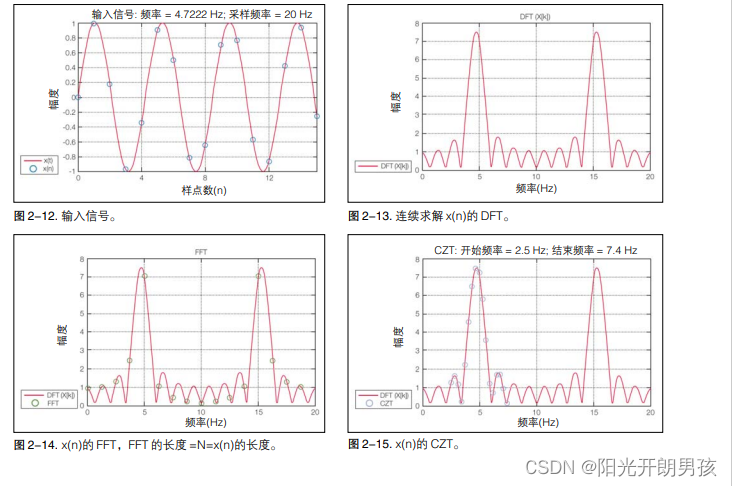
为说明 DFT 与 FFT 及 CZT 的关系，我们将分析一个采样的连续波(CW)信号。为清楚起见，我们将使用实数值的正弦波 x(t)作为输入信号(图 2-12)。x(t)的采样版本是 x(n)。在这种情况下，N = 16，采样率是 20 Hz。

图 2-13显示了对0 ≤ k < N，DFT的求解结果。注意，对 Ω > Π (f > 10 Hz)，X[k]的幅度是上半部分的镜像。这是实数值输入序列x(n)的结果。在实践中，在分析实际输入信号时，会丢掉(或不计算) Π< Ω < 2 Π的结果。对复数输入，对0 ≤ Ω < 2 Π (0 ≤ f < 20 Hz)可以获得唯一的结果。

FFT 返回 X[k]的 N 个等间隔频域样点。X[k]的幅度如图2-14所示。注意，FFT返回的样点可能会漏掉X[k]的幅度峰值。

CZT可以返回带有任意开始频率和结束频率的M个频域样点(图2-15)。注意，CZT不会改变DFT的底层频域输出。它只会提取与 FFT 不同的一套频域样点。

使用CZT的优势是可以任意选择频域中第一个样点和最后一个样点的频率，而不依赖于输入采样率。通过任意控制输入采样率，以便FFT的输出得到与CZT相同的输出样点，也可以获得相同的结果。在这两种情况下，最终结果是相同的。选择纯粹是实现问题，根据要求和可用的硬件，这两种方案都可能都是次优解决方案。

数字滤波

有限脉冲响应(FIR)滤波器
许多应用使用频率滤波器，选择某些频率，拒绝其它频率。传统滤波器使用模拟电路单元(RLC)实现，而DSP则以数学方式选择要增强或衰减的频率。一种常见的数学实现方式是有限脉冲响应(FIR)滤波器。RSA全面使用FIR滤波器。除要求传送或拒绝特定频段的普通信号调节应用外，FIR滤波器还可以用来调节模拟信号路径的不理想特点。内部生成的对准数据与存储的工厂校准数据结合在一起，创建其响应补偿模拟信号路径频响的FIR滤波器，使模拟路径和数字路径级联拥有平坦的幅度响应和线性相位。

频响与脉冲响应
傅立叶变换定理说明了频域和时域之间具有同等性。它进一步告诉我们，设备的转函(通常用随频率变化的幅度和相位响应表示)等于测量期间的脉冲响应。FIR滤波器使用时间周期有限的离散时间近似方法，仿真所需滤波转函的脉冲响应。然后通过使用滤波器的脉冲响应对输入信号求卷积，执行信号滤波。

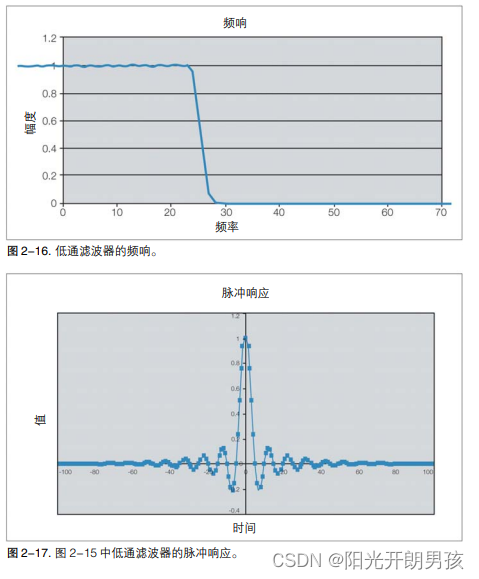
图 2-16 显示了低通滤波器的转函幅度。图 2-17 显示了其脉冲响应。

数值卷积

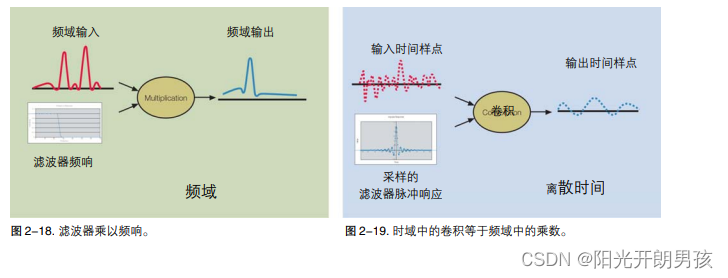
频域通常用来分析线性系统的响应，如滤波器。信号用频率成分表示。通过把输入信号频谱乘以滤波器的频响，计算得出滤波器输出上的信号频谱。图 2-18 说明了频域操作。傅立叶定理指出，频域中的乘数等于时域中的卷积。上图中的频域乘数等于使用滤波器的脉冲响应对输入信号的时域表示求卷积，如图 2-19 所示。

所有频率滤波器都需要使用存储器单元。模拟滤波器中常用的无功单元带有存储器，因为其在电路中的输出取决于电流输入及各个时点上的输入。可以使用图 2-20所示的实际存储器单元，构建离散时间滤波器。

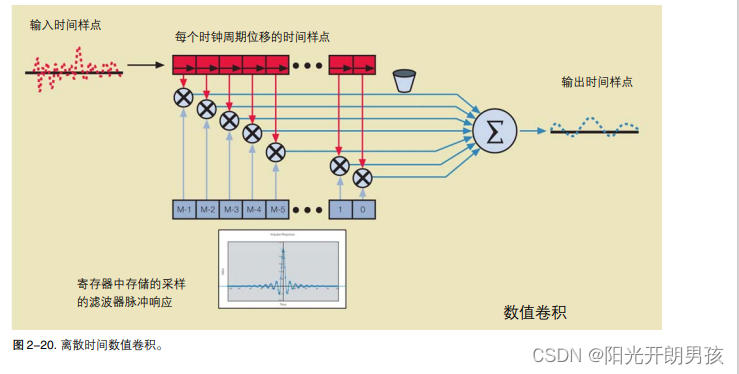
下方寄存器用来存储滤波器的脉冲响应值，较早的样点在右面，较晚的样点在左面。上方寄存器用来把输入信号从左面移到右面，每个时钟周期位移一次。每个对应寄存器的内容乘在一起，得到的所有乘积每个时钟周期加总一次，加总的结果得到滤波后的信号。

总之，RSA在频谱分析中严重依赖数字信号处理。适用于 RSA 的 DSP 要点包括：RSA6000 使用 FFT 和 CZT 组合，实现频谱显示。
1）FFT的计算效率更高，可以实现更快的变换速率，而CZT 要更加灵活，可以为一套固定的输入样点提供可变的解析带宽。
2）通过在执行傅立叶变换前对时域信号应用优化的窗口函数，可以实现解析带宽(RBW)形状。RBW 由 3 dB带宽和 60 dB:3 dB 形状系数指定，指定方式与模拟实现方案相同。一般来说，数字实现的滤波器的形状系数要低于(急剧于)模拟实现方案，可以更简便地解析相距很近的幅度差异很大的信号。

通过应用优化的窗口函数，其它形状系数可以用于特定应用。

在执行频谱分析时，RSA3000 系列RSA 结合使用多种方法。
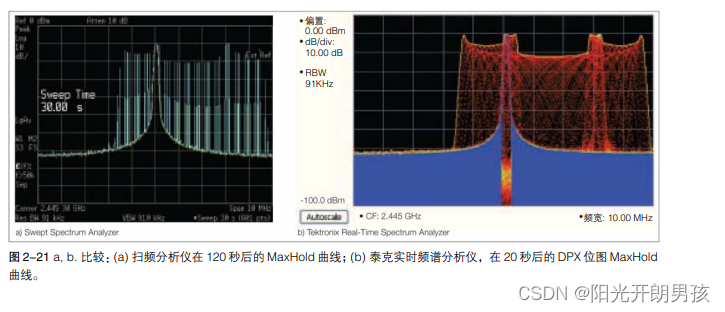
1）在Spectrum模式下，开窗口的FFT的结果使用RBW形状求卷积，得到具有指定RBW的Spectrum曲线，这与模拟频谱分析仪类似。这一过程得到大约5:1的形状系数，略宽于 RSA6000 的 4.1:1。
2）在 DPX 模式下，CZT 用于解析带宽灵活性。
3） 在RSA模式下，使用开窗口的FFT，在FFT分析的典型方法中指定噪声带宽。噪声带宽大约比RBW高6%(0.25 dB)。