Stochastic order notation(随机有序符号)

大Op(big oh-pee),或者用代数术语记为$O_p$，是用来表示随机变量序列的概率收敛的一种速记方法。

大$O_p$意味着，某些给定的随机变量是随机有界的。若$X_n$为某个随机变量，$a_n$表示某些常数，其中n表示序列的索引符号，则
$$X_n=O_p(a_n)$$
等同于说，
$$P(|\frac{X_n}{a_n}|>\delta )<ϵ,\forall n>N$$.

其中$\delta$和$N$是有限的数，$ϵ$是某个任意（小）的数。$O_p$意味着当$n$足够大时，存在某个数（$\delta$）使得随机变量$\frac{X_n}{a_n}$大于$\delta$的概率基本为0.它是“bounded in probability”(可能翻译为：依概率有界)(Vaart 1998, sec.2.2).

小$o_p$（little oh_pee）是指依概率收敛到0。
$$X_n=o_p(1)$$
等同于说，
$$\underset{n\to \infty }{\lim }P(|X_n|\ge ϵ)=0,\forall ϵ>0.$$

根据$o_p$的定义，如果$X_n=o_p(a_n)$，则$\frac{X_n}{a_n}=o_p(1).$反过来，我们可以将$X_n=o_p(a_n)$表示为
$$\underset{n\to \infty }{\lim }P(|\frac{X_n}{a_n}|\ge ϵ)=0,\forall ϵ>0.$$
换句话说，$X_n=o_p(a_n)$当且仅当$$\frac{X_n}{a_n}\stackrel{p}{⟶}0.$$

6.1.1$O_p$和$o_p$之间的关系

看上去$O_p$和$o_p$很像，那是因为它们确实很像！
另一种表达$X_n=O_p(a_n)$的方式是通过数学语言，即
$$\forall ϵ>0,\exists N_{ϵ},{\delta }_{ϵ},s.t.\forall n>N_{ϵ},P(|\frac{X_n}{a_n}|\ge {\delta }_{ϵ})\le ϵ.$$

上述这种数学语言表达形式清楚地表明，$N$和$\delta$的选择与$ϵ$有关，即对于每个$ϵ$，可以在该$ϵ$下，找到满足上述不等式的$N$和$\delta$。不同的$ϵ$下， $N$和$\delta$值可以是不同的。

同样，我们可以使用相同的数学语言表示$X_n=o_p(a_n)$，即
$$\forall ϵ,\delta ,\exists N_{ϵ,\delta },s.t.\forall n>N_{ϵ,\delta },P(|\frac{X_n}{a_n}|\ge \delta )\le ϵ.$$

因此，从上述关于$O_p$和$o_p$的数学语言表达可以看出，$o_p$是一个更general的说法，因为$o_p$涵盖了（1）$ϵ$和$\delta$所有值，以及（2）$ϵ$和$\delta$的任意组合。此外，通过上述数学语言表达可以看出，$o_p（a_n)$蕴含着$O_p(a_n)$，即如果$X_n=o_p(a_n)$，那么一定有$X_n=O_p(a_n)$。因为，根据$o_p$的数学语言表达，对于任意的$ϵ$和$\delta$都可以找到满足上述不等式的$N$，那么对任意的$ϵ$，可以从上述任意的$\delta$中找到要给$\delta$以及$N$，使得有不等式成立。但是，仅仅对某个$\delta$有不等式成立，这不意味着对所有的$\delta$，不等式都成立。

6.2 符号速记及其算数性质

像$X_n=o_p(\frac{1}{\sqrt{(}n)})$的表达不包含任意的文字。$O_p$和$o_p$只是用来表达随机变量序列如何收敛（要么收敛到一个bound,要么收敛到0）。

例如，假设$X_n=o_p(\frac{1}{n})$，因此我们也直到$X_n=o_p(\frac{1}{n^{0.5}})$.类似的，想象一个物体以至少10$m{s}^{-2}$的速度加速，那辆车也在以至少$5m{s}^{-2}$.但是，并不是说$o_p\frac{1}{n}=o_p(\frac{1}{n^{0.5}})$.例如，加速至少5$m{s}^{-2}$的汽车不一定加速至少10$m{s}^{-2}$。

因此，当我们使用这些随机顺序符号时（stochastic order notation,准确的翻译没有查），我们应该认为这些$o_p$和$O_p$意味着什么，而不是说随机变量序列或者包含随机变量的表达式等于某个$o_p$和$O_p$.

下面给出$O_p$与$o_p$组合项的含义：

• $o_p(1)+o_p(1)=o_p(1)$：这两项都是以相同的速率收敛到0，那么其和以该速率收敛到0. 注意到，这是连续映射定理（continuous mapping theorem）的一个简单应用。因为，如果$X_n=o_p(1),Y_n=o_p(1)$，则$X_n\stackrel{p}{⟶0},Y_n\stackrel{p}{⟶0}$,则由两项的相加是一个连续映射函数，因此，$X_n+Y_n\stackrel{p}{⟶}0$，所以$X_n+Y_n=o_p(1).$
• $O_p(1)+o_p(1)=O_p(1)$：一个依概率有界的项 加上 依概率收敛到0的项，等于依概率有界。
• $O_p(1)o_p(1)=o_p(1)$：一个依概率有界的项 乘以 (以相同顺序)依概率收敛到0的项等于依概率收敛到0.
• $o_p(R)=R\times o_p(1)$：这很容易看出，因为如果$X_n=o_p(R)$,则$X_n/R=o_p(1)$,因此，$X_n=R{o}_p(1)$.

进一步的规则和对其有效性的直观解释可以在Vaart (1998)的第2.2节中找到。

然而，上述最后一条规则值得简单的讨论以下，因为它清楚的说明了，为什么我们在$o_p$算子中使用不同的速度rate项R。

考虑两个速度rate$R^{(1)}=\frac{1}{\sqrt{(}n)}$,$R^{(2)}=\frac{1}{2^{\frac{1}{3}}}$,随机变量序列$Y_n\stackrel{p}{⟶0}$，即$Y_n=o_p(1)$.

根据上述最后一条性质，并且我们要时刻记住，其中等号不应该按照字面意思来理解。

若$X_n^{(1)}=o_p(R^{(1)})$，则
$$X_n^{(1)}=\frac{1}{\sqrt{n}}\times Y_n,$$

若$X_n^{(2)}=o_p(R^{(2)})$,则
$$X_n^{(2)}=\frac{1}{n^{\frac{1}{3}}}\times Y_n,$$

当$n$趋于无穷时，对于$Y_n$的每个值，$X_n^{(1)}$比$X_n^{(2)}$小，换句话说，$X_n^{(1)}$收敛于0的速度更快。

6.3 为什么$o_p$和$O_p$符号很有用？

这里我们通过一个简单的例子对此进行说明。考虑一个随机变量序列$X_n$，其期望为$E(X_n)=X$,因此$X_n=X+o_p(1)$，根据弱大数定律（weak law of large numbers）知$X_n\stackrel{p}{⟶X}$。这是非常有用的，因为我们不必在方程中引入明确的极限，在$X_n=X+o_p(1)$中的第二项收敛于零，因此我们可以忽略它。

考虑一个更有意义的例子。若$X_n\sim N(0,n)$。根据正态分布的性质知，
$$\frac{X_n}{\sqrt{(}n)}\sim N(0,1)$$

存在某个$M$使得从$N(0,1)$中生成的某个数超过$M$的概率小于$ϵ>0$，因此
$$X_n=O_p(\sqrt{(}n))$$

同时$X_n=o_p(n)$。

下面我们证明$X_n=o_p(n)$。

由于
$$\frac{X_n}{n}\sim N(0,\frac{n}{n^2})=N(0,\frac{1}{n})$$

我们只需要证明$N(0,\frac{1}{n})=o_p(1)$即可，这样有$\frac{X_n}{n}=o_p(1)$，进而$X_n=n{o}_p(1)=o_p(n)$。

注意到
$$P(|N(0,\frac{1}{n})|>ϵ)=P(\frac{1}{\sqrt{(}n)}|N(0,1)|>ϵ)=P(|N(0,1)|>\sqrt{(}n)ϵ)\stackrel{p}{⟶0}$$

最后一项成立，是因为$\sqrt{(}n)\to \infty$，故来自标准正态分布的数大于∞的概率降低到0，因此$X_n=o_p(n)$

使用大O和小o表示，捕捉了方程的复杂性，或者等价地捕捉了方程收敛的速度。一种理解$X_n=o_p(a_n)$的方式是，$X_n$通过由$a_n$确定的速度收敛到0。例如，$o_p(a_n^2)$的收敛速度比$o_p(a_n)$快，因为对随机变量序列$X_n$，$\frac{X_n}{a_n^2}<\frac{X_n}{a_n},n>1$.

当我们想要计算一个更复杂的方程的渐近极限时，其中多个项受到观测个数（即样本量）的影响。如果我们有一个项比其他项更快的依概率收敛到0，那么我们完全可以忽略这个项。

6.4例子：均值估计的相合性

如果一个参数的估计量，随着样本量n的增加，参数的估计量依概率收敛到一个参数，则该估计量是“相合的”（consistent）。更正式的表示为，一个参数估计$\hat{\theta }$是相合估计，若
$$P(|\hat{\theta }-\theta |\ge ϵ)\stackrel{p}{⟶0}$$
其中$\theta$是参数真值。

一个感兴趣的问题：我们的这个相合估计向参数真值收敛的速度如何。这个一个“应用”方法的问题，为寻求对参数真值进行推断，对这个参数，我们可能得到许多不同的估计量，我么希望从中挑选一个有效的估计量，即一个能最快达到参数真值的估计量。

假如我们想要估计$X$的总体均值，即$\bar{X}$。此时我们有两个潜在的估计量，样本均值$\frac{1}{N}{\sum }_{i=1}^N{X}_i$，中位数$X_{(N+1)/2}$，其中$N=2n+1$.(为了便于计算，我们假设样本量N为奇数)，X是从小到大的有序序列。

由中心极限定理知，样本均值
$${\bar{X}}_N\sim N(0,\frac{{\delta }^2}{N})$$

不需要证明可以给出，中位数估计量的大样本分布可以近似地表示为：
$$Med(X_1,X_2,\cdots ,X_N)\sim N(\theta ,\frac{\pi {\delta }^2}{2N})$$.

这些估计量在实践中表现如何？我们通过蒙特卡洛模拟来进行说明。通过模拟，我们可以绘制上述两个估计量的最终分布。

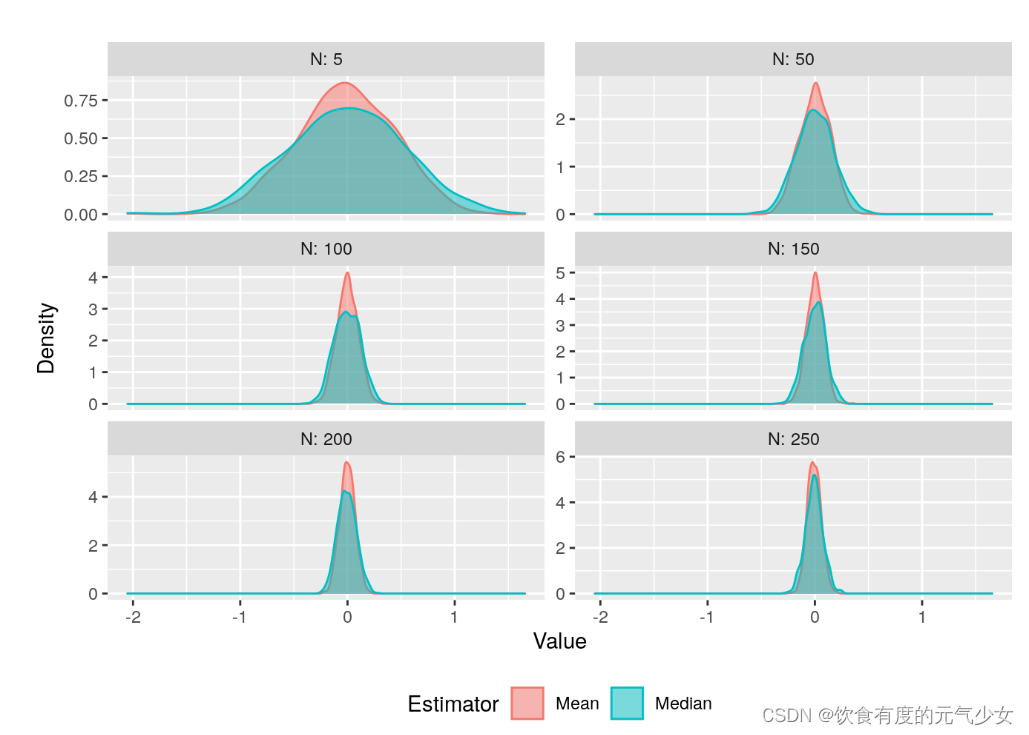
从图中我们可以看到，这两个估计量都是服从正态分布，样本均值分布的方差比样本中位数估计量的方差收缩的快，也就是说，样本中位数估计量的方差比样本均值的方差大，从图中我们可以看到，绿色（表示中位数估计量）图像是扁平的，红色(均值估计量)是瘦长的，红色取值相对较集中，绿色取值相对较分散，说明绿色的方差大。换句话说，红色的估计更有效。这里的有效性体现了我们在数学上提到的，样本均值收敛到参数真值的收敛速度比中位数估计量收敛到参数真值的收敛速度快！

值得注意的是，上述两个估计量都是无偏估计，都是服从正态分布，并且都是相合估计（随着样本量的增加，估计量向参数真值收敛），但是方差缩小的速度略有不同。

我们可以使用$o_p$符号在大样本下，对这些估计量进行刻画。

首先，我们定义均值估计的估计误差和中位数估计的估计误差，即
$${\psi }_{Mean}=\hat{\theta }-\theta =N(0,\frac{{\delta }^2}{N})-N(\theta ,0)=N(0,\frac{{\delta }^2}{N}).$$

$${\psi }_{Med}=N(\theta ,\frac{\pi {\delta }^2}{2N})-N(\theta ,0)=N(0,\frac{\pi {\delta }^2}{2N}).$$

从上面的表达式中，我们可以看到，估计量的估计误差以0为中心，估计量是无偏的。

根据本章前面的讨论，我们可以对上述两个估计量重新进行改写，以找出这两个估计量的收敛到参数真值的速度。

$${\psi }_{Mean}=\frac{1}{\sqrt{(}N)}N(0,{\delta }^2)$$
$$\frac{{\psi }_{Mean}}{N^{-0.5}}=N(0,{\delta }^2).$$

我们知道，对于一个正态分布，存在某个$M_{ϵ}$和$N_{ϵ}$，使得
$$P(|N(0,{\delta }^2)|\ge M_{ϵ}<ϵ)$$,
因此，${\psi }_{Mean}=O_p(\frac{1}{\sqrt{(}N)}).$

类似的，对于样本中位数：

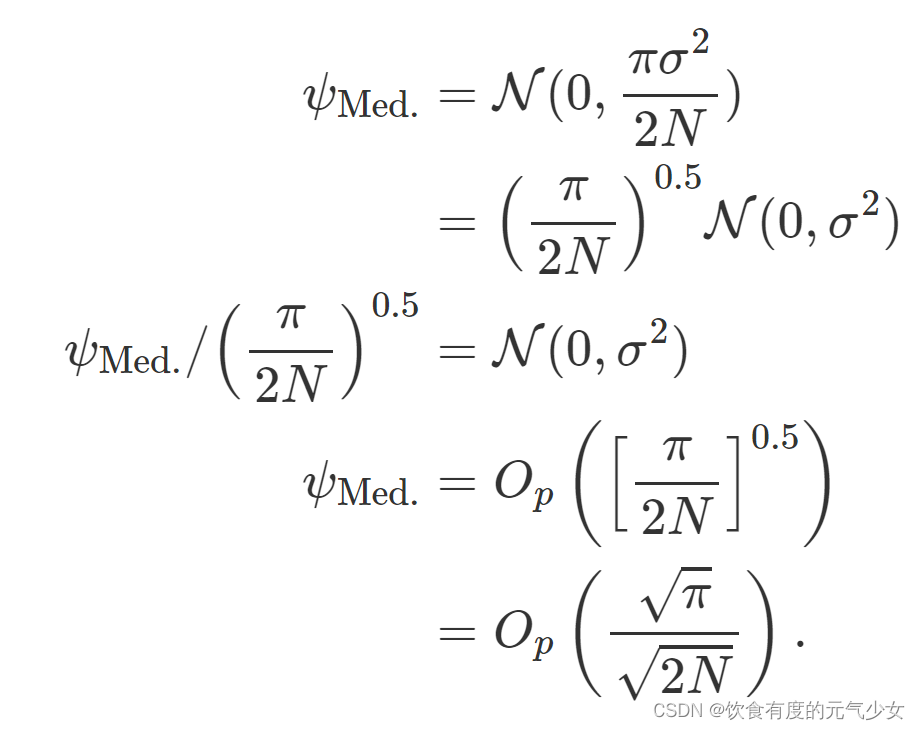
因此，我们可以看到${\psi }_{Med}$比${\psi }_{Mean}$要慢，意味着Mean比Med需要更少的样本量就可以收敛到参数真值。

参考：

https://bookdown.org/ts_robinson1994/10_fundamental_theorems_for_econometrics/big-op-and-little-op.html