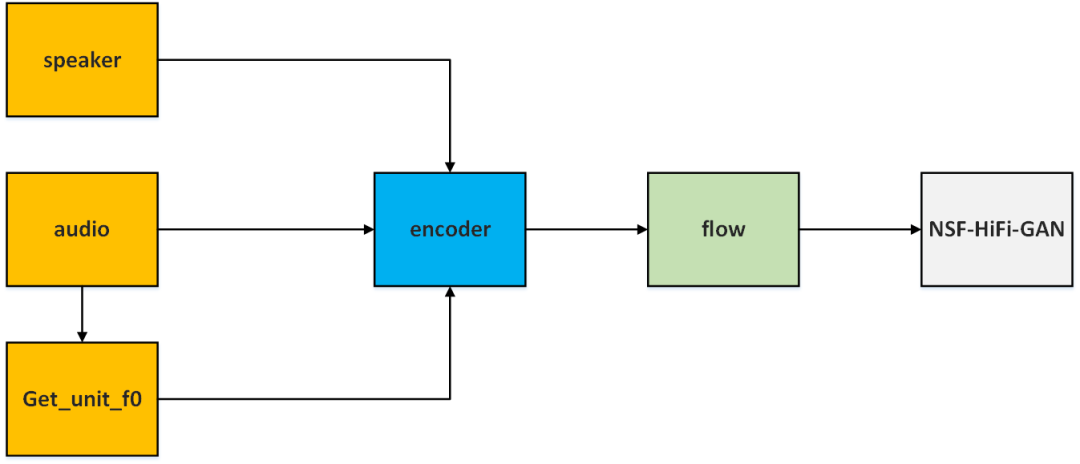
涉及积分的定理
分部积分
分部积分:
∫
a
b
u
(
x
)
v
′
(
x
)
d
x
=
u
(
x
)
v
(
x
)
∣
a
b
−
∫
a
b
v
(
x
)
u
′
(
x
)
d
x
\int_a^bu(x)v'(x)dx=u(x)v(x)|_a^b-\int_a^bv(x)u'(x)dx
∫abu(x)v′(x)dx=u(x)v(x)∣ab−∫abv(x)u′(x)dx
其中, v ′ ( x ) = d v d x v'(x) = \frac{dv}{dx} v′(x)=dxdv
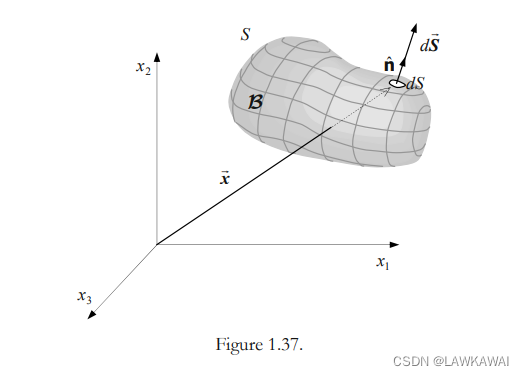
散度定理
给定一个体积为V的域B,边界为S,那么应用在向量场的散度定理(也叫Green’s Theorem, 格林定理)为:
∫
V
∇
x
⃗
⋅
v
⃗
d
V
=
∫
S
v
⃗
⋅
n
^
d
S
=
∫
S
v
⃗
⋅
d
S
⃗
∫
V
v
i
,
i
d
V
=
∫
S
v
i
n
^
i
d
S
=
∫
S
v
i
d
S
i
\int_V \nabla_{\vec x}\cdot \vec vd V = \int_S \vec v\cdot \hat ndS = \int _S \vec v\cdot d\vec S \\ \int_V v_{i,i}dV=\int_Sv_i\hat n_idS=\int_Sv_idS_i
∫V∇x⋅vdV=∫Sv⋅n^dS=∫Sv⋅dS∫Vvi,idV=∫Svin^idS=∫SvidSi
其中,
n
^
\hat n
n^ 是向外垂直于表面S的
令T是在域B的二阶张量场,那么应用散度定理在这个场:
∫
V
∇
x
⃗
⋅
T
d
V
=
∫
S
T
⋅
n
^
d
S
=
∫
S
T
⋅
d
S
⃗
∫
V
T
i
j
,
j
d
V
=
∫
S
T
i
j
n
^
j
d
S
=
∫
S
T
i
j
d
S
j
\int_V \nabla_{\vec x}\cdot Td V = \int_S T\cdot \hat ndS = \int _S T\cdot d\vec S \\ \int_V T_{ij,j}dV=\int_ST_{ij}\hat n_jdS=\int_ST_{ij}dS_j
∫V∇x⋅TdV=∫ST⋅n^dS=∫ST⋅dS∫VTij,jdV=∫STijn^jdS=∫STijdSj
通过利用散度定理,也可以证明:
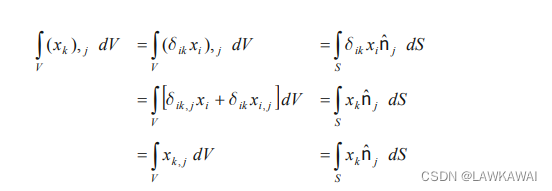
其中,假设
δ
i
k
,
j
=
0
i
k
j
\delta_{ik,j}=0_{ikj}
δik,j=0ikj,另外,因为
x
k
,
j
=
δ
k
j
x_{k,j}=\delta_{kj}
xk,j=δkj,得到:
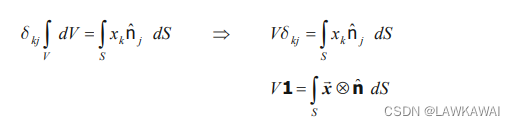
给定一个定义在域B的二阶张量,以下成立:
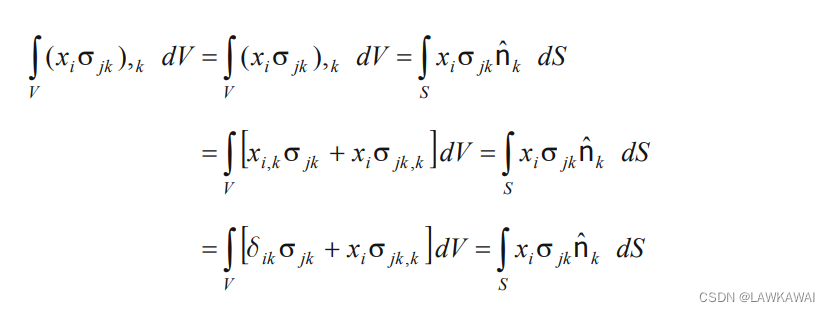
因此,可以证明:
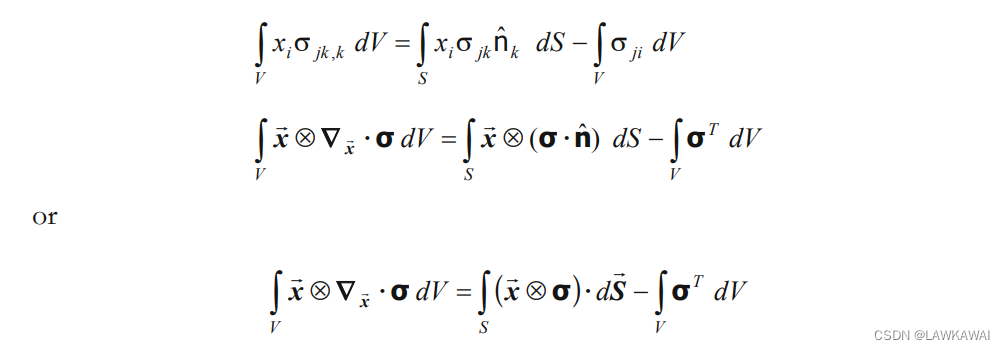
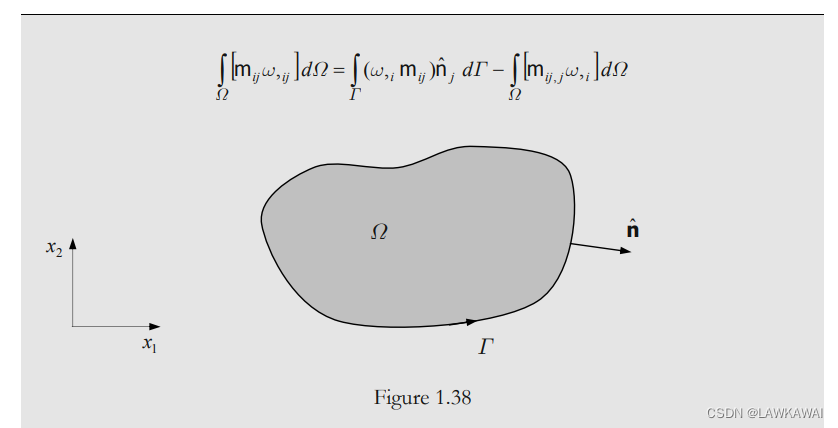
问题1.47 令 Ω \Omega Ω 是一个边界为 Γ \Gamma Γ的域,m是一个二阶张量场, ω \omega ω是一个标量场,证明:



路径的独立性
连接两个点A和B的曲线称为从A到B的路径

建立线积分与路径无关的条件:
令
b
⃗
(
x
⃗
)
\vec b(\vec x)
b(x)是一个连续的向量场,那么积分
∫
C
b
⃗
⋅
d
r
⃗
\int_{C}\vec b\cdot d\vec r
∫Cb⋅dr与路径无关,当且仅当
b
⃗
\vec b
b是保守场,这意味着存在一个标量场
ϕ
\phi
ϕ使得
b
⃗
=
∇
x
⃗
ϕ
\vec b = \nabla_{\vec x} \phi
b=∇xϕ,也就是向量场是某个标量场的梯度:
∫
A
B
b
⃗
⋅
d
r
⃗
=
∫
A
B
∇
x
⃗
ϕ
⋅
d
r
⃗
∫
A
B
(
b
1
e
^
1
+
b
2
e
^
2
+
b
3
e
^
3
)
⋅
d
r
⃗
=
∫
A
B
(
∂
ϕ
∂
x
1
e
^
1
+
∂
ϕ
∂
x
2
e
^
2
+
∂
ϕ
∂
x
3
e
^
3
)
⋅
d
r
⃗
\int_A^B\vec b\cdot d\vec r=\int_A^B\nabla_{\vec x}\phi \cdot d\vec r \\ \int_A^B(b_1\hat e_1+b_2\hat e_2+b_3\hat e_3)\cdot d\vec r=\int_A^B(\frac{\partial \phi}{\partial x_1}\hat e_1+\frac{\partial \phi}{\partial x_2}\hat e_2+\frac{\partial \phi}{\partial x_3}\hat e_3)\cdot d\vec r
∫ABb⋅dr=∫AB∇xϕ⋅dr∫AB(b1e^1+b2e^2+b3e^3)⋅dr=∫AB(∂x1∂ϕe^1+∂x2∂ϕe^2+∂x3∂ϕe^3)⋅dr
因此:
b
1
=
∂
ϕ
∂
x
1
;
b
2
=
∂
ϕ
∂
x
2
;
b
3
=
∂
ϕ
∂
x
3
;
b_1 = \frac{\partial \phi}{\partial x_1}; \quad b_2 = \frac{\partial \phi}{\partial x_2}; \quad b_3 = \frac{\partial \phi}{\partial x_3};
b1=∂x1∂ϕ;b2=∂x2∂ϕ;b3=∂x3∂ϕ;
由于场是保守的,所以
b
⃗
\vec b
b的旋度为0:
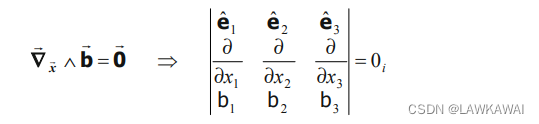
因此,得出结论:
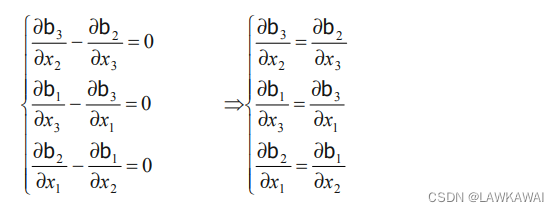
因此,如果以上条件不满足,则场不是保守的
Kelvin-Stokes定理
令S是一个曲面,
F
⃗
(
x
⃗
,
t
)
\vec F(\vec x, t)
F(x,t)是一个向量场,根据Kelvin-Stokes定理,有:
∮
Γ
F
⃗
⋅
d
Γ
⃗
=
∫
Ω
(
∇
⃗
x
⃗
∧
F
⃗
)
⋅
d
S
⃗
=
∫
Ω
(
∇
⃗
x
⃗
∧
F
⃗
)
⋅
n
^
d
S
\boxed{\oint_{\Gamma}\vec F \cdot d\vec \Gamma=\int_{\Omega}(\vec \nabla_{\vec x}\wedge \vec F)\cdot d\vec S=\int_{\Omega}(\vec \nabla_{\vec x}\wedge \vec F)\cdot \hat n dS}
∮ΓF⋅dΓ=∫Ω(∇x∧F)⋅dS=∫Ω(∇x∧F)⋅n^dS
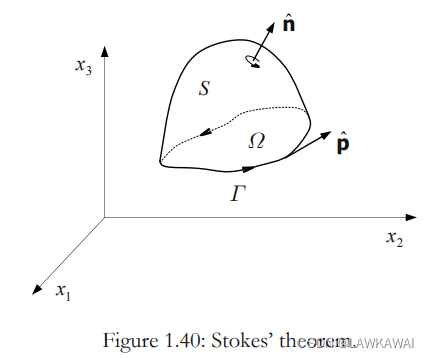
如果
p
^
\hat p
p^表示切向于边界
Γ
\Gamma
Γ的单位向量,那么Stoke’s定理为:
∮
Γ
F
⃗
⋅
p
^
d
Γ
=
∫
Ω
(
∇
⃗
x
⃗
∧
F
⃗
)
⋅
d
S
⃗
=
∫
Ω
(
∇
⃗
x
⃗
∧
F
⃗
)
⋅
n
^
d
S
\oint_{\Gamma}\vec F\cdot \hat pd \Gamma=\int_{\Omega}(\vec \nabla_{\vec x}\wedge \vec F)\cdot d\vec S=\int_{\Omega}(\vec \nabla_{\vec x}\wedge \vec F)\cdot \hat ndS
∮ΓF⋅p^dΓ=∫Ω(∇x∧F)⋅dS=∫Ω(∇x∧F)⋅n^dS
参考笛卡尔坐标系下的表示:
F
⃗
=
F
1
e
^
1
+
F
2
e
^
2
+
F
3
e
^
3
\vec F= F_1 \hat e_1+ F_2 \hat e_2+ F_3 \hat e_3
F=F1e^1+F2e^2+F3e^3
d
S
⃗
=
d
S
1
e
^
1
+
d
S
2
e
^
2
+
d
S
3
e
^
3
d\vec S = dS_1\hat e_1+dS_2\hat e_2+dS_3\hat e_3
dS=dS1e^1+dS2e^2+dS3e^3
d
Γ
⃗
=
d
x
1
e
^
1
+
d
x
2
e
^
2
+
d
x
3
e
^
3
d\vec \Gamma = dx_1\hat e_1+dx_2\hat e_2+dx_3\hat e_3
dΓ=dx1e^1+dx2e^2+dx3e^3
F
⃗
\vec F
F的旋度的分量为:
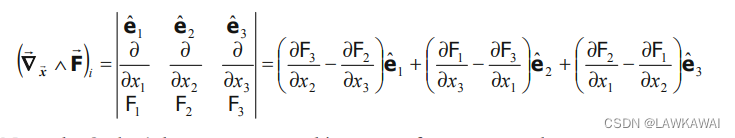
那么,Stoke‘s定理表示成以上分量形式:
∮
Γ
F
1
d
x
1
+
F
2
d
x
2
+
F
3
d
x
3
=
∫
Ω
(
∂
F
3
∂
x
2
−
∂
F
2
∂
x
3
)
d
S
1
+
(
∂
F
1
∂
x
3
−
∂
F
3
∂
x
1
)
d
S
2
+
(
∂
F
2
∂
x
1
−
∂
F
1
∂
x
2
)
d
S
3
\oint_{\Gamma}F_1dx_1+F_2dx_2+F_3dx_3 \\ =\int_{\Omega}(\frac{\partial F_3}{\partial x_2}-\frac{\partial F_2}{\partial x_3})dS_1+(\frac{\partial F_1}{\partial x_3}-\frac{\partial F_3}{\partial x_1})dS_2+(\frac{\partial F_2}{\partial x_1}-\frac{\partial F_1}{\partial x_2})dS_3
∮ΓF1dx1+F2dx2+F3dx3=∫Ω(∂x2∂F3−∂x3∂F2)dS1+(∂x3∂F1−∂x1∂F3)dS2+(∂x1∂F2−∂x2∂F1)dS3
特殊情况:曲面S是就是平面
Ω
\Omega
Ω,上式仍然成立
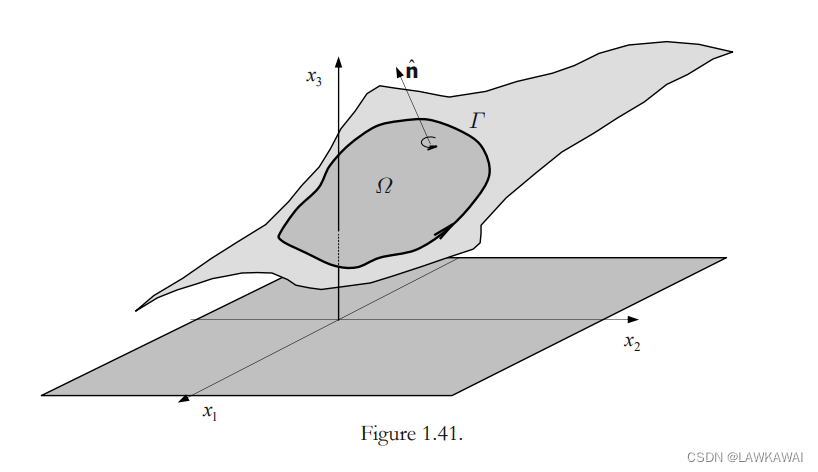
如果
Ω
\Omega
Ω是
x
1
−
x
2
x_1-x_2
x1−x2平面,那么上式变为:
∮
Γ
F
⃗
⋅
d
Γ
=
∫
Ω
(
∇
⃗
x
⃗
∧
F
⃗
)
⋅
e
^
3
d
S
\oint_{\Gamma}\vec F \cdot d \Gamma=\int_{\Omega}(\vec \nabla_{\vec x}\wedge \vec F)\cdot \hat e_3 dS
∮ΓF⋅dΓ=∫Ω(∇x∧F)⋅e^3dS
这就是大家都知道的平面上的Stoke’s定理,即格林公式。
张量分量:
∮
Γ
F
1
d
x
1
+
F
2
d
x
2
=
∫
Ω
(
∂
F
2
∂
x
1
−
∂
F
1
∂
x
2
)
d
S
3
\oint_{\Gamma}F_1dx_1+F_2dx_2=\int_{\Omega}(\frac{\partial F_2}{\partial x_1}-\frac{\partial F_1}{\partial x_2}) dS_3
∮ΓF1dx1+F2dx2=∫Ω(∂x1∂F2−∂x2∂F1)dS3
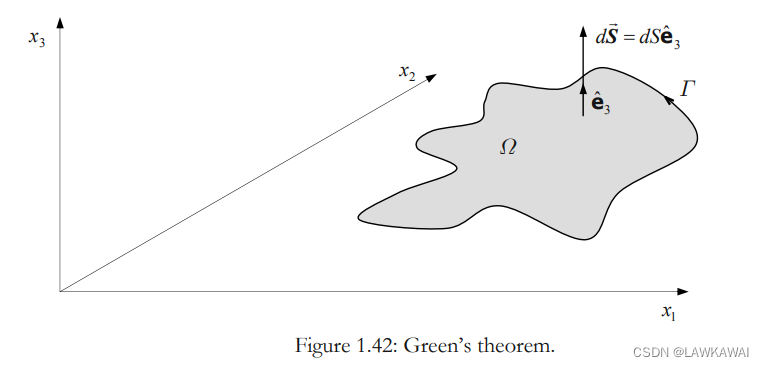
格林公式
令
F
⃗
\vec F
F是一个向量场,应用散度定理,有:
∫
V
∇
x
⃗
⋅
F
⃗
=
∫
S
F
⃗
⋅
n
^
d
S
\int_V \nabla_{\vec x}\cdot \vec F=\int_S \vec F \cdot \hat n dS
∫V∇x⋅F=∫SF⋅n^dS
根据:

令
F
⃗
=
ϕ
∇
x
⃗
ψ
\vec F = \phi \nabla_{\vec x}\psi
F=ϕ∇xψ,代入上面两个等式:
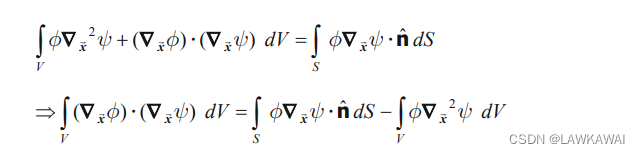
这就是格林第一公式
且有:

这就是格林第二公式
问题1.48 令 b ⃗ \vec b b是一个向量场,定义为 b ⃗ = ∇ ⃗ x ⃗ ∧ v ⃗ \vec b =\vec \nabla_{\vec x}\wedge \vec v b=∇x∧v,证明:

参考教材:
Eduardo W.V. Chaves, Notes On Continuum Mechanics