【数据结构】二叉树顺序结构、链式结构的实现、遍历二叉树（前序 中序 后序 层序）

news2025/1/11 21:40:15

文章目录

  • 1.二叉树结构实现
    • 1.1顺序结构的实现
    • 1.2链式结构的实现
  • 2.堆的概念和介绍
  • 3.二叉树的遍历
    • 3.1前序遍历
    • 3.2中序遍历
    • 3.3后序遍历
    • 3.4层序遍历

1.二叉树结构实现

1.1顺序结构的实现

  在之前的文章中，我们对二叉树有了一定的了解，这里我们会对二叉树再进行一些内容的补充。

  普通的二叉树是不适合用数组来存储的，因为可能会存在大量的空间浪费。而完全二叉树更适合使用顺序结构存储。
  现实中我们通常把堆(一种二叉树)使用顺序结构的数组来存储，需要注意的是这里的堆和操作系统虚拟进程地址空间中的堆是两回事，一个是数据结构，一个是操作系统中管理内存的一块区域分段。
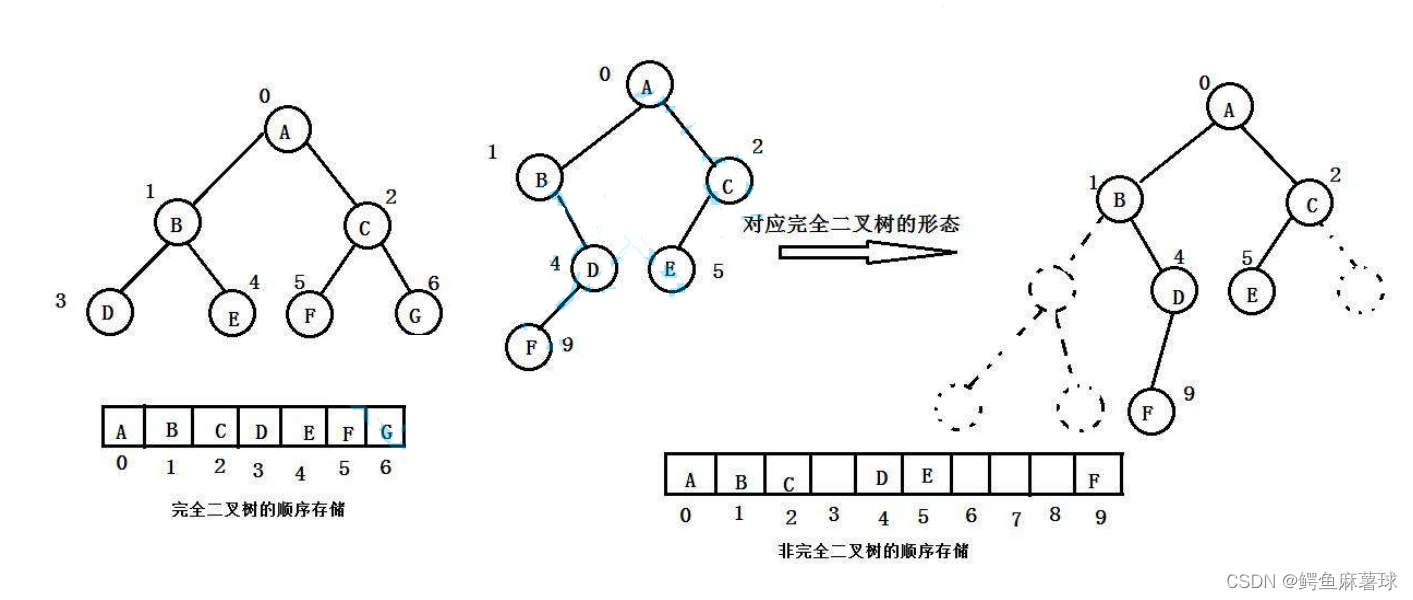
在这里插入图片描述
 
在C语言定义一个简单顺序二叉树：

// 顺序存储结构二叉树
typedef struct {
    int data[MAX_TREE_SIZE + 1];   // 数组存储结构
    int size;                      // 当前二叉树的大小
} SeqBinaryTree;

//堆
typedef int HPDataType;
typedef struct Heap
{
	HPDataType* _a;
	int _size;
	int _capacity; 
}Heap;

 
  虽然二叉树结构不完整的情况下，需要预留足够的空间，可能会浪费部分存储空间，但是在实际应用中，顺序结构二叉树还是运用的较为广泛，完全二叉树的存储和操作，用于堆排序、哈夫曼编码等算法的实现。
  以下是顺序结构二叉树的优点：

  （1）实现简单：使用数组实现，不需要内存动态分配，也不需要链表结构复杂的指针操作，实现简单。

  （2）存储方便：可以将完全二叉树按顺序存储，不需要为每个结点存储指针信息，节省空间。

  （3）存储结构稳定：由于整个二叉树在一块连续的内存中，顺序存储结构的稳定性优于链式存储结构，不容易出现内存泄漏或内存碎片等问题。

  （4）访问效率高：由于顺序结构二叉树是连续存储的，可以通过下标快速访问任意结点，访问效率高。

  （5）空间利用率高：在完全二叉树的情况下，顺序结构二叉树的空间利用率非常高，每个节点的位置都是有意义的，不需要浪费额外的空间。
 

顺序结构二叉树的实现（参考）

#include <stdio.h>
#include <stdlib.h>

#define MAX_TREE_SIZE 100

// 顺序存储结构二叉树
typedef struct {
    int data[MAX_TREE_SIZE + 1];   // 数组存储结构，下标从1开始
    int size;                      // 当前二叉树的大小
} SeqBinaryTree;

// 初始化二叉树
void init(SeqBinaryTree *tree) {
    tree->size = 0;
}

// 判断二叉树是否为空
int is_empty(SeqBinaryTree *tree) {
    return tree->size == 0;
}

// 返回二叉树的元素个数
int size(SeqBinaryTree *tree) {
    return tree->size;
}

// 获取二叉树的根结点
int get_root(SeqBinaryTree *tree) {
    if (is_empty(tree)) {
        printf("Binary tree is empty.\n");
        exit(0);
    }
    return tree->data[1];
}

// 获取指定节点的父亲节点
int get_parent(SeqBinaryTree *tree, int index) {
    if (is_empty(tree)) {
        printf("Binary tree is empty.\n");
        exit(0);
    } else if (index == 1) {
        printf("This node is root, no parent node.\n");
        exit(0);
    }
    return tree->data[index / 2];
}

// 获取指定节点的左儿子节点
int get_left_child(SeqBinaryTree *tree, int index) {
    if (is_empty(tree)) {
        printf("Binary tree is empty.\n");
        exit(0);
    } else if (index * 2 > tree->size) {
        printf("This node does not have a left child.\n");
        exit(0);
    }
    return tree->data[index * 2];
}

// 获取指定节点的右儿子节点
int get_right_child(SeqBinaryTree *tree, int index) {
    if (is_empty(tree)) {
        printf("Binary tree is empty.\n");
        exit(0);
    } else if (index * 2 + 1 > tree->size) {
        printf("This node does not have a right child.\n");
        exit(0);
    }
    return tree->data[index * 2 + 1];
}

// 插入节点
void insert(SeqBinaryTree *tree, int data) {
    if (tree->size >= MAX_TREE_SIZE) {
        printf("Binary tree is full.\n");
        exit(0);
    }
    tree->size++;
    tree->data[tree->size] = data;
}

// 销毁二叉树
void destroy(SeqBinaryTree *tree) {
    tree->size = 0;
    printf("Binary tree has been destroyed.\n");
}

 

1.2链式结构的实现

用C语言简单定义一个链式二叉树

typedef int BTDataType;
typedef struct BinaryTreeNode
{
 BTDataType _data;
 struct BinaryTreeNode* _left;
 struct BinaryTreeNode* _right;
}BTNode;

 

链式结构的二叉树有以下优点：

  （1）结构灵活：链式二叉树的结构比较灵活，可以根据实际情况动态调整，不需要预先确定容量大小。

  （2）空间利用率高：链式二叉树在节点不规则的情况下，可以避免像顺序结构二叉树那样浪费大量的存储空间，空间利用率较高。

  （3）插入和删除效率高：链式结构二叉树在节点插入和删除操作时，不需要像顺序结构二叉树那样移动大量的节点，因此其插入和删除效率更高。

  （4）实际使用灵活：在实际应用中，链式二叉树可以非常容易地实现出友好的API（例如用C++实现模板化的二叉树），或在容器内部作为辅助数据结构来完成各种复杂功能。

  链式结构二叉树一般适用于非满二叉树/不规则二叉树的情况，在树的结点数量和深度变化频繁的情况下，链式二叉树更能体现出其优点。尤其是对于二叉搜索树等数据结构，链式二叉树使用起来更加方便，也更加实用一些。
 

链式结构二叉树的实现（参考）

#include<stdio.h>
#include<stdlib.h>

struct node {
    int data;  //节点的值
    struct node *left;  //指向左子节点的指针
    struct node *right;  //指向左子节点的指针
};

//插入节点的函数
struct node* insert(struct node* root, int data) {
    //如果根节点为空，新建一个节点并将它作为根节点
    if (root == NULL) {
        root = (struct node*)malloc(sizeof(struct node));
        root->data = data;
        root->left = NULL;
        root->right = NULL;
    }
    //如果节点不为空，则比较它和当前节点的值，决定向左或向右插入
    else {
        if (data < root->data) {
            root->left = insert(root->left, data);
        } else if (data > root->data) {
            root->right = insert(root->right, data);
        }
    }
    return root;
}

//中序遍历函数
void inorder(struct node *root) {
    if (root == NULL) {
        return;
    }
    inorder(root->left);
    printf("%d ", root->data);
    inorder(root->right);
}

int main() {
    struct node *root = NULL;
    root = insert(root, 9);
    insert(root, 6);
    insert(root, 15);
    insert(root, 3);
    insert(root, 8);
    insert(root, 12);
    insert(root, 18);
    printf("中序遍历结果：");
    inorder(root);
    printf("\n");
    return 0;
}

 

2.堆的概念和介绍

  堆就是顺序结构二叉树。

  如果有一个关键码的集合K = { K0，K1 ，K2 ，K3…，Kn-1 }，把它的所有元素按完全二叉树的顺序存储方式存储在一个一维数组中，并满足：Ki<=K2i+1 且Ki<= K2i+2 (Ki >=K2i+1 且 Ki>=K2i+2 ) i = 0，1，2…，则称为小堆(或大堆)。将根节点最大的堆叫做最大堆或大根堆，根节点最小的堆叫做最小堆或小根堆。

堆有以下性质：
 （1）堆中某个节点的值总是不大于或不小于其父节点的值；
 （2）堆总是一棵完全二叉树。

 
堆的C语言简单实现（参考）

#include <stdio.h>

#define MAX_HEAP_SIZE 100

typedef struct {
    int data[MAX_HEAP_SIZE];
    int size;
} MaxHeap;

// 插入元素
void insert(MaxHeap *heap, int value) {
    int i = ++(heap->size);
    while (i != 1 && value > heap->data[i/2]) {
        heap->data[i] = heap->data[i/2];
        i = i/2;
    }
    heap->data[i] = value;
}

// 删除堆顶元素
int delete(MaxHeap *heap) {
    if (heap->size == 0) {
        printf("堆已经为空，无法继续删除！\n");
        return -1;
    }

    int max = heap->data[1];
    int last = heap->data[heap->size--];
    int i = 1, child;
    while (i*2 <= heap->size) {
        child = i*2;
        if (child+1 <= heap->size && heap->data[child+1] > heap->data[child])
            child++;
        if (last < heap->data[child])
            heap->data[i] = heap->data[child];
        else
            break;
        i = child;
    }
    heap->data[i] = last;
    return max;
}

// 查找堆顶元素
int find_max(MaxHeap heap) {
    if (heap.size == 0) {
        printf("堆已经为空！\n");
        return -1;
    }

    return heap.data[1];
}

// 堆排序
void heap_sort(MaxHeap *heap) {
    while (heap->size != 0) {
        printf("%d ", delete(heap));
    }
}

int main() {
    MaxHeap heap = {{0}, 0};
    insert(&heap, 6);
    insert(&heap, 12);
    insert(&heap, 8);
    insert(&heap, 15);
    insert(&heap, 5);
    insert(&heap, 10);

    printf("堆排序结果：");
    heap_sort(&heap);
    printf("\n");

    return 0;
}

 

3.二叉树的遍历

  所谓二叉树遍历(Traversal)是按照某种特定的规则，依次对二叉树中的节点进行相应的操作，并且每个节点只操作一次。访问结点所做的操作依赖于具体的应用问题。 遍历是二叉树上最重要的运算之一，也是二叉树上进行其它运算的基础。
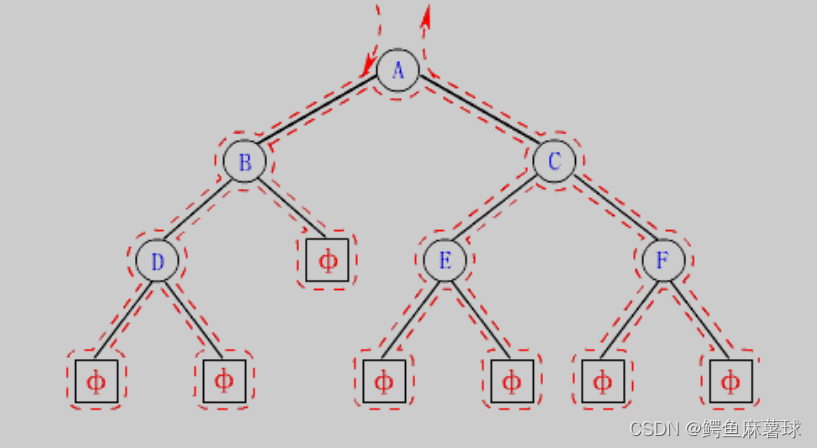
在这里插入图片描述
按照规则，二叉树的遍历有：前序/中序/后序的递归结构遍历：

（1）前序遍历(Preorder Traversal 亦称先序遍历)——访问根结点的操作发生在遍历其左右子树之前。
（2）中序遍历(Inorder Traversal)——访问根结点的操作发生在遍历其左右子树之中（间）。
（3）后序遍历(Postorder Traversal)——访问根结点的操作发生在遍历其左右子树之后。

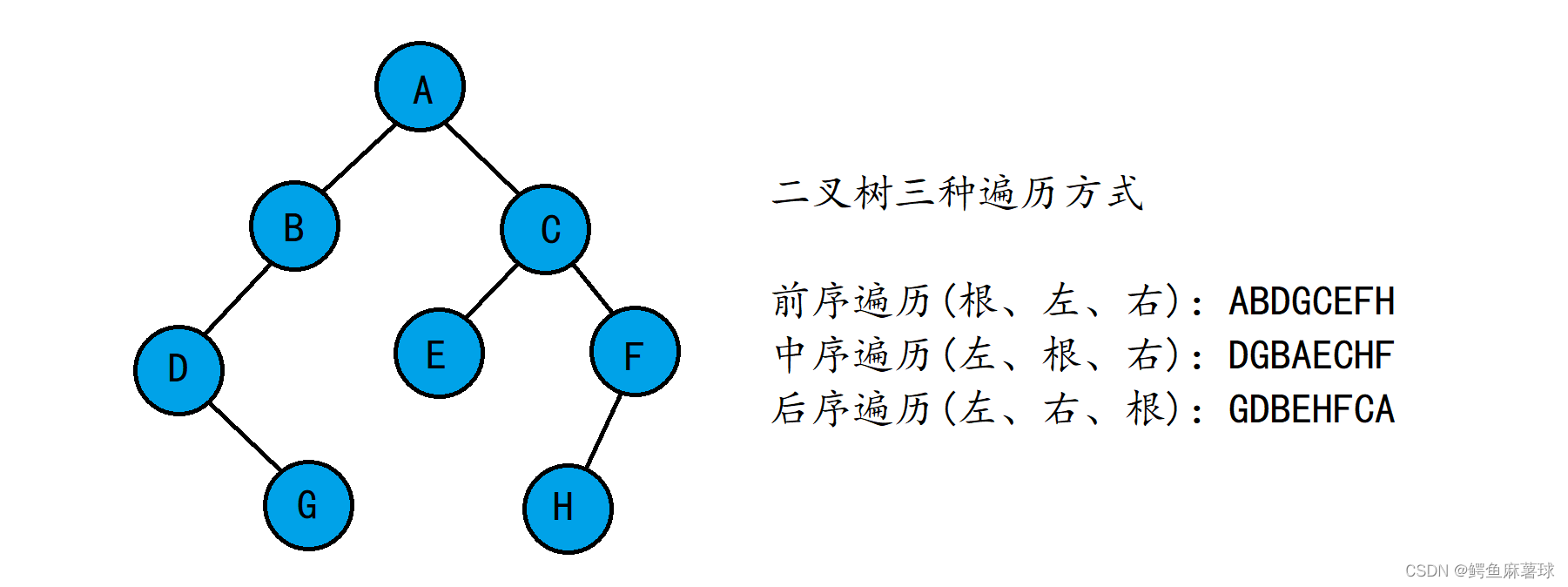
在这里插入图片描述

3.1前序遍历

  二叉树的前序遍历是指按照 根节点-左子树-右子树  的遍历顺序，遍历整棵树。可以使用递归或迭代算法实现前序遍历。
 
C语言递归实现前序遍历：

struct TreeNode {
    int val;
    struct TreeNode *left;
    struct TreeNode *right;
};

void preorderTraversal(struct TreeNode* root){
    if(root == NULL){
        return;
    }
    printf("%d ", root->val);  // 访问根节点
    preorderTraversal(root->left);  // 递归左子树
    preorderTraversal(root->right);  // 递归右子树
}

C语言迭代算法使用栈实现：

void preorderTraversal(struct TreeNode* root){
    if(root == NULL){
        return;
    }

    struct TreeNode *stack[1000];  // 定义一个栈
    int top = 0;
    stack[top++] = root;  // 将根节点压入栈中

    while(top > 0){
        struct TreeNode *p = stack[--top];  // 弹出栈顶元素
        printf("%d ", p->val);  // 访问根节点

        if(p->right){  // 先将右子树节点压入栈中
            stack[top++] = p->right;
        }
        if(p->left){  // 将左子树节点压入栈中
            stack[top++] = p->left;
        }
    }
}

 

3.2中序遍历

  二叉树的前序遍历是指按照 左节点-根子树-右子树  的遍历顺序，遍历整棵树。可以使用递归或迭代算法实现前序遍历。
 
C语言递归实现中序遍历：

struct TreeNode {
    int val;
    struct TreeNode *left;
    struct TreeNode *right;
};

void inorderTraversal(struct TreeNode* root){
    if(root == NULL){
        return;
    }
    inorderTraversal(root->left);  // 递归左子树
    printf("%d ", root->val);  // 访问根节点
    inorderTraversal(root->right);  // 递归右子树
}

C语言迭代算法使用栈实现：

void inorderTraversal(struct TreeNode* root){
    if(root == NULL){
        return;
    }

    struct TreeNode *stack[1000];  // 定义一个栈
    int top = 0;
    struct TreeNode *p = root;

    while(p != NULL || top > 0){
        while(p != NULL){  // 将左子树节点压入栈中
            stack[top++] = p;
            p = p->left;
        }

        if(top > 0){  // 弹出栈顶元素
            p = stack[--top];
            printf("%d ", p->val);  // 访问根节点
            p = p->right;  // 将右子树节点压入栈中
        }
    }
}

 

3.3后序遍历

  二叉树的前序遍历是指按照 左节点-右子树-根子树  的遍历顺序，遍历整棵树。可以使用递归或迭代算法实现前序遍历。
 
C语言递归实现后序遍历：

struct TreeNode {
    int val;
    struct TreeNode *left;
    struct TreeNode *right;
};

void postorderTraversal(struct TreeNode* root){
    if(root == NULL){
        return;
    }
    postorderTraversal(root->left);  // 递归左子树
    postorderTraversal(root->right);  // 递归右子树
    printf("%d ", root->val);  // 访问根节点
}

C语言迭代算法使用栈实现：

void postorderTraversal(struct TreeNode* root){
    if(root == NULL){
        return;
    }

    struct TreeNode *stack1[1000];  // 定义两个栈
    struct TreeNode *stack2[1000];
    int top1 = 0, top2 = -1;
    struct TreeNode *p = root;

    while(p != NULL || top1 > 0){  // 遍历所有节点
        while(p != NULL){  // 先将左子树入栈1
            stack1[top1++] = p;
            stack2[++top2] = 0;  // 将当前节点在栈2中标记为未访问
            p = p->left;
        }

        while(top1 > 0 && stack2[top2] == 1){  // 当栈1非空且栈顶节点在栈2中已经被标记时，弹出节点并访问
            p = stack1[--top1];
            printf("%d ", p->val);
            top2--;
        }

        if(top1 > 0){  // 将栈顶节点右子节点入栈1，并在栈2中标记为未访问
            p = stack1[top1-1]->right;
            stack2[top2] = 1;
        }
        else{  // 如果栈1为空，则遍历结束
            break;
        }
    }
}

 

3.4层序遍历

  二叉树的层序遍历是指按照树的层次  顺序逐层遍历 即从上到下，从左到右遍历每一层的所有节点。可以通过队列来实现二叉树的层序遍历。

C语言队列实现层序遍历：

struct TreeNode {
    int val;
    struct TreeNode *left;
    struct TreeNode *right;
};

void levelOrderTraversal(struct TreeNode* root){
    if(root == NULL){
        return;
    }

    struct TreeNode *queue[1000];  // 定义一个队列
    int front = 0, rear = 0;
    queue[rear++] = root;  // 将根节点入队

    while(front < rear){  // 队列非空时循环
        struct TreeNode *p = queue[front++];  // 取出队首节点并访问
        printf("%d ", p->val);

        if(p->left){  // 将左子节点入队
            queue[rear++] = p->left;
        }
        if(p->right){  // 将右子节点入队
            queue[rear++] = p->right;
        }
    }
}

这些就是数据结构中有关二叉树实现和遍历的简单介绍了😉
如有错误❌望指正，最后祝大家学习进步✊天天开心✨🎉

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/561317.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

el-table实现可拖拽移动列和动态排序字段

el-table实现可拖拽移动列和动态排序字段

&#x1f37f;*★,*:.☆(&#xffe3;▽&#xffe3;)/$:*.★* &#x1f37f; &#x1f35f;欢迎来到前端初见的博文&#xff0c;本文主要讲解在工作中以一个案例el-table实现可拖拽移动列和动态排序字段&#x1f35f; &#x1f468;‍&#x1f527; 个人主页 : 前端初见 &…
阅读更多...
chatgpt赋能Python-python_nanmean

chatgpt赋能Python-python_nanmean

Python的nanmean函数&#xff1a;用于计算数组的平均值 Python引入的nanmean函数是一种快速而有效的计算数组平均值的方法。与其他Python中的平均值函数不同&#xff0c;nanmean函数可以处理NaN值&#xff0c;即缺失值。在数据科学和统计学中&#xff0c;处理缺失值是一个常见…
阅读更多...
chatgpt赋能Python-python_nontype

chatgpt赋能Python-python_nontype

介绍Python中的NoneType: 完整的解释和实例 在Python编程中&#xff0c;有一个特殊的数据类型叫做"NoneType"&#xff0c;它通常被简称为"None"。这个数据类型被用于表示没有值或空值&#xff08;null&#xff09;。在本文中&#xff0c;我们将探索NoneTy…
阅读更多...
1.4集合的运算定律

1.4集合的运算定律

阅读更多...
Spring(五大类注解，对象的三种注入方式及其优缺点)

Spring(五大类注解，对象的三种注入方式及其优缺点)

目录 1.存储 Bean 对象 1.1前置工作:配置扫描路径 1.2添加注解存储 Bean 对象 1.2.1 Controller [控制器存储] 1.2.2 Service&#xff08;服务存储&#xff09; 1.2.3 Repository&#xff08;仓库存储&#xff09; 1.2.4 Component&#xff08;组件存储&#xff09; 1.…
阅读更多...
chatgpt赋能Python-python_os怎么用

chatgpt赋能Python-python_os怎么用

Python OS模块&#xff1a;让你的文件操作更高效 在Python编程中&#xff0c;文件和文件夹的操作是非常常见的&#xff0c;例如创建、删除、修改、读取等等。这些任务都需要使用操作系统的命令&#xff0c;但是如果每次都手动调用操作系统命令&#xff0c;这样会使编程效率低下…
阅读更多...
Vulkan Tutorial 2 presentation

Vulkan Tutorial 2 presentation

目录 5 窗口表面 6 交换链 7 图像视图 5 窗口表面 由于Vulkan是一个与平台无关的API&#xff0c;它自己不能直接与窗口系统对接。为了在Vulkan和窗口系统之间建立连接&#xff0c;将结果呈现在屏幕上&#xff0c;我们需要使用WSI&#xff08;窗口系统集成&#xff09;扩展。…
阅读更多...
【瑞萨RA_FSP】DMAC/DTC——直接存储器访问与数据传输

【瑞萨RA_FSP】DMAC/DTC——直接存储器访问与数据传输

文章目录 一、DMAC和DTC模块简介1. DMAC 特性2. DTC 特性 二、DMAC 模块框图分析三、DMAC 传输模式1. 正常传输模式2. 重复传输模式3. 块传输模式4. 重复-块传输模式 四、DTC 模块框图分析五、DTC 传输模式1. 正常传输模式2. 重复传输模式3. 块传输模式 六、DMAC和DTC关键特性对…
阅读更多...
WMS 概述 -- “窗口管理员“

WMS 概述 -- “窗口管理员“

WMS 概述 -- "窗口管理员" 1、WMS 职责2、涉及元素3、WMS、AMS与Activity间的关系 1、WMS 职责 WMS职责理解窗口管理WMS 是窗口的管理者&#xff0c;它负责窗口的启动、添加和删除&#xff0c;另外窗口的大小和层级也是由WMS 进行管理的。窗口管理的核心成员有 Disp…
阅读更多...
结构体总结

结构体总结

目录 1.普通结构体 2.定义结构体并同时建立变量 3.匿名结构体 4.typedef重命名 5.typedef省略结构体名字 6.结构体数组 7.结构体指针 8.结构体嵌套 9.结构体链表&#xff08;头插法&#xff09; 10.结构体中的函数指针 11.结构体的构造函数和初始化列表 1.普通结构体 stru…
阅读更多...
chatgpt赋能Python-python_paas

chatgpt赋能Python-python_paas

Python PaaS&#xff1a;简介和未来趋势 随着云计算的不断普及&#xff0c;PaaS&#xff08;平台即服务&#xff09;正在成为越来越受欢迎的选择。PaaS可以帮助企业轻松构建、部署和管理应用程序&#xff0c;无需担心底层基础架构的问题。在PaaS领域&#xff0c;Python正在成为…
阅读更多...
2023年护网蓝队初级面试总结

2023年护网蓝队初级面试总结

00.护网面试步骤是什么样的 投递简历-安全服务公司HR先筛选一下简历&#xff0c;交给技术负责人面试一下&#xff0c;推荐给安全厂商&#xff08;360、奇安信、安恒、绿盟&#xff09; 安全设备厂商HR筛选一下简历&#xff0c;安全设备厂商安排技术笔试和面试&#xff08;技术…
阅读更多...
Kubernetes高可用集群二进制部署（Runtime Docker）v1.21版本

Kubernetes高可用集群二进制部署（Runtime Docker）v1.21版本

Kubernetes高可用集群二进制部署&#xff08;Runtime Docker&#xff09; Kubernetes&#xff08;简称为&#xff1a;k8s&#xff09;是Google在2014年6月开源的一个容器集群管理系统&#xff0c;使用Go语言开发&#xff0c;用于管理云平台中多个主机上的容器化的应用&#xf…
阅读更多...
chatgpt赋能Python-python_num怎么用

chatgpt赋能Python-python_num怎么用

Python Num怎么用&#xff1f;一个有10年Python编程经验的工程师来告诉你 Python是一种被广泛应用的编程语言&#xff0c;它的发展历程已经超过了20年。而其中的NumPy库则成为了Python编程中最重要的一部分之一。NumPy是一个Python库&#xff0c;它提供了大量针对数字的操作函…
阅读更多...
AI宝典：AI超强工具大整合

AI宝典：AI超强工具大整合

&#x1f604;&#x1f604;个人介绍 光子郎.进行开发工作七年以上&#xff0c;目前涉及全栈领域并进行开发。会经常跟小伙伴分享前沿技术知识&#xff0c;java后台、web前端、移动端&#xff08;Android&#xff0c;uniapp&#xff0c;小程序&#xff09;相关的知识以及经验体…
阅读更多...
微服务实战项目-学成在线-项目介绍以及环境搭建

微服务实战项目-学成在线-项目介绍以及环境搭建

学成在线-项目介绍&环境搭建 1.项目背景 1.1 在线教育市场环境 以下内容摘自https://report.iresearch.cn/content/2021/01/358854.shtml 在线教育行业是一个有着极强的广度和深度的行业&#xff0c;从校内到校外&#xff1b;从早幼教到职业培训&#xff1b;从教育工具…
阅读更多...
Prometheus（普罗米修斯）

Prometheus（普罗米修斯）

Prometheus : 入门 Prometheus简介Prometheus 的主要特点Prometheus架构&#xff1a;什么时候用它合适什么时候用它不合适Prometheus VS InfluxDB基本概念数据模型metric types&#xff08;指标类型&#xff09; Prometheus 安装部署二进制安装部署1、将安装包prometheus-2.6.1…
阅读更多...
stable-diffusion-webui(1.2.1版本) win10系统本地电脑部署

stable-diffusion-webui(1.2.1版本) win10系统本地电脑部署

在安装stable-diffusion-webui(1.2.1版本)之前需要确认win10本地电脑具有的环境 1.显卡类型&#xff1a;NVIDIA&#xff08;英伟达&#xff09; 建议显存高于4G以上&#xff0c;这样512*512的还是可以运行的 2.python(版本必须最好是3.10.6&#xff09;和 git最新版 正式…
阅读更多...
【MySQL高级篇笔记 (上) 】

【MySQL高级篇笔记 (上) 】

此笔记为尚硅谷MySQL高级篇部分内容 目录 一、MySQL的数据目录 小结 二 、用户与权限管理 MySQL8密码管理(了解) 权限管理 授予权限的原则 收回权限 权限表 访问控制(了解) 角色管理 三、逻辑架构 服务器处理客户端请求 MySQL 中的 SQL执行流程 SQL语法顺序…
阅读更多...
chatgpt赋能Python-python_numpy画图

chatgpt赋能Python-python_numpy画图

Python Numpy画图&#xff1a;快速绘制高质量的数据可视化 Python语言不仅在数据科学和人工智能领域得到广泛应用&#xff0c;还被广泛用于数据可视化方面。NumPy是一个Python的科学计算库&#xff0c;提供了高性能的多维数组对象和广播功能&#xff0c;被广泛应用于数据科学、…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023